Решение различный типов задач с параметром

Реферат на тему «Решение задач с параметром»

Подготовил ученик 11 класса МБОУ «Лицей «Интеллект» города Донецка»

Руководитель Мигинская Людмила Михайловнвна

→

2

Что такое параметр?

• Параметр  - это независимая переменная, значение которой считается заданным, фиксированным или произвольным действительным числом, или числом принадлежащим заранее оговоренному множеству (неизвестным, но фиксированным).

→

←

3

Основные типы задач с парметром:

• Уравнения, которые надо решить для любого значения параметра, либо для значений параметра, принадлежащих заранее оговоренному множеству.
• Например, решить уравнение:

→

←

4

Основные типы задач с параметром:

• Уравнения, в которых надо определить кол-во решений в зависимости от a
• Например, при каких a уравнение имеет единственный корень.

→

←

5

Основные типы задач с параметром:

• Уравнения в которых при искомых значениях параметра a множество решений удовлетворяет заданным условиям в ОДЗ
• Например, найти a при которых корни уравнения положительные

→

←

6

Что значит решить уравнение с параметром?

• Решить уравнение с параметром f(x;a)=0 – значит решить семейство уравнений f(x;a)=0 для любых действительных значений параметра a. Решить каждое уравнение из бесконечного семейства невозможно, но можно это сделать, разбив множество значений параметра на подмножества по некоторому целесообразному признаку и решить его на них. Для разбиения полезно воспользоваться теми значениями параметра, при которых или при переходе через которые происходит качественное изменение уравнения, такие значения параметра называют контрольными или особыми. Искусство решения уравнений с параметром как раз и состоит в том, чтобы находить эти контрольные значения параметра.

→

←

7

Что значит решить уравнение с параметром?

• Для разбиения полезно воспользоваться теми значениями параметра, при которых или при переходе через которые происходит качественное изменение уравнения, такие значения параметра называют контрольными или особыми. Искусство решения уравнений с параметром как раз и состоит в том, чтобы находить эти контрольные значения параметра .

→

←

8

Основные методы решения задач с параметрами:

• Аналитический(способ прямого решения), т.е. способ стандартного решение. Он самый сложный.

→

←

9

Основные методы решения задач с параметрами:

• Графический. Построение графиков левой и правой части уравнения в координатной плоскости XoY или Xoa.

→

←

10

Основные методы решения задач с параметрами:

• Решение относительно параметра: при нем переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение является более простым

→

←

11

Линейные уравнения с параметром и приводимые к ним:

• любое линейное уравнение с параметрами элементарными преобразованиями может быть приведено к виду  aх=b , где  a  и  b  – некоторые выражения, хотя бы одно из которых содержит параметр и  исследуется по схеме:

  aх=b

a =0

a ≠0

B-люб

x=b/ a

b=0

b ≠0

один корень

0x=0

0x=b

x-люб

x=Ø

←

→

12

Линейные уравнения с параметром и приводимые к ним:

• В процессе решения выделяем значения а =0,

при которых происходит качественное изменение уравнения (т.е. находим контрольное

или особое значение параметра)

Пример 1: для каждого значения параметра а решить уравнение а 2 x-1=x+ a

• Приводим уравнение к виду ax=b

a 2 x-x=a+1; (a 2 -1)x=a+1;

• Находим контрольное значение параметра:

a 2 -1=0; (a-1)(a+1)=0; a=1 или a=-1

a=1, 0x=2, x= Ø; a =-1, 0x=0, x-люб; a ≠1 и a ≠-1, x=

a +1

1

( a +1)( a -1)

a -1

=

→

←

13

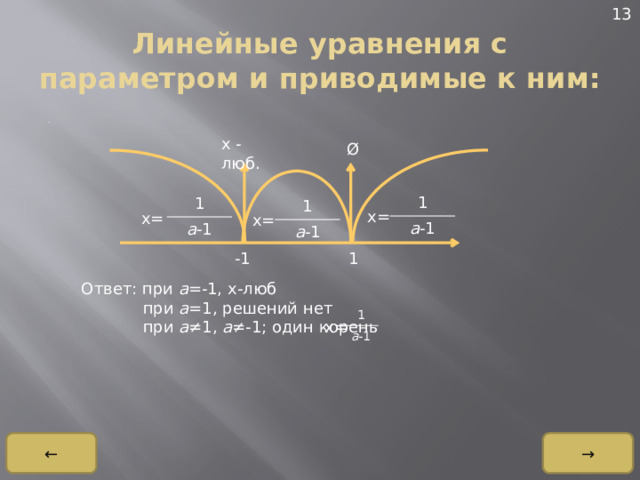
Линейные уравнения с параметром и приводимые к ним:

.

x - люб.

Ø

1

a -1

1

a -1

1

a -1

x=

x=

x=

-1

1

Ответ: при а =-1, x-люб

при а =1, решений нет

при а ≠ 1, а ≠ -1; один корень

1

a -1

x=

←

→

a = ±1 2) Если a =1 ур-е принимает вид: 0x=-4 = x=Ø 3) Если a =-1 ур-е принимает вид: 0x=0 = x-любое 4) Если a ≠±1 ур-е принимает вид: a -3 a -1 a 2 -2 a -3 ( a +1)( a -3) a 2 -1 ( a -1)( a +1) = = x= ← → " width="640"

14

Уравнения с парарметром при наличии дополнительных условий

• Задача №1. При каких значениях a уравнение

( a 2 -1)x= a 2 -2 a -3 имеет единственное решение на луче

[-1;+ ∞ ]

1) Находим контрольные точки параметра:

a 2 -1=0 = a = ±1

2) Если a =1 ур-е принимает вид:

0x=-4 = x=Ø

3) Если a =-1 ур-е принимает вид:

0x=0 = x-любое

4) Если a ≠±1 ур-е принимает вид:

a -3

a -1

a 2 -2 a -3

( a +1)( a -3)

a 2 -1

( a -1)( a +1)

=

=

x=

←

→

( a -1)( a -2) ≥0 - + + ////// ////// 2 1 Ответ: a є (- ∞ ; 1) U [2; + ∞ ) ← → " width="640"

15

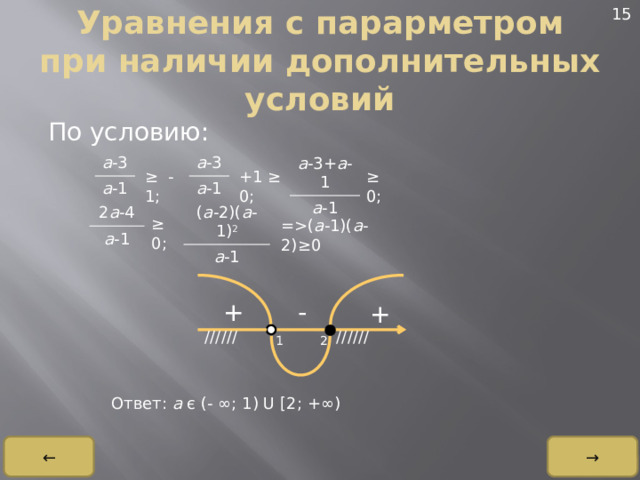
Уравнения с парарметром при наличии дополнительных условий

По условию:

a -3

a -3

a -1

a -1

a -3+ a -1

a -1

+1 ≥ 0;

≥ -1;

≥ 0;

( a -2)( a -1) 2

a -1

2 a -4

a -1

≥ 0;

=( a -1)( a -2) ≥0

-

+

+

//////

//////

2

1

Ответ: a є (- ∞ ; 1) U [2; + ∞ )

←

→

0 D=0 Dx = - c b Корней нет x 1 = x 2 = X 1,2 = -b -b ±√D 2a 2a При решении квадратного уравнения с параметром контрольными будут те значения параметра, при которых коэффициент при x 2 равен 0. Т.е. уравнение превращается в линейное и действуем по алгоритму для решения линейных уравнений, если коэффициент ≠ 0, дальнейшее решение зависит от D. → ← " width="640"

16

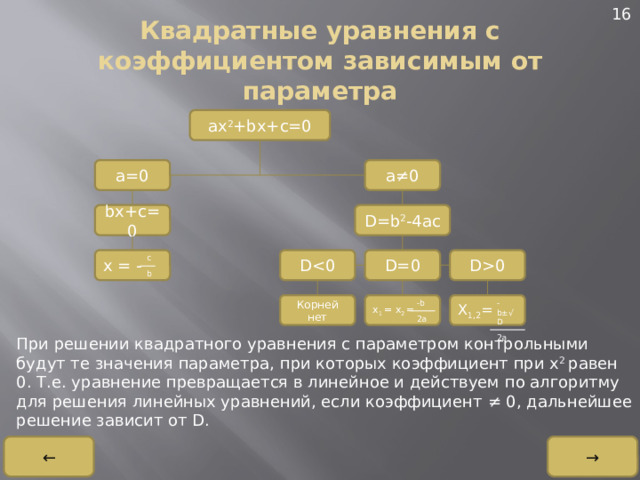
Квадратные уравнения с коэффициентом зависимым от параметра

ax 2 +bx+c=0

a=0

a ≠0

bx+c=0

D=b 2 -4ac

D0

D=0

D

x = -

c

b

Корней нет

x 1 = x 2 =

X 1,2 =

-b

-b ±√D

2a

2a

При решении квадратного уравнения с параметром контрольными будут те значения параметра, при которых коэффициент при x 2 равен 0. Т.е. уравнение превращается в линейное и действуем по алгоритму для решения линейных уравнений, если коэффициент ≠ 0, дальнейшее решение зависит от D.

→

←

4x=-5 = x= 2) Если a ≠2. D = 4 a 2 -4( a -2)( a +3) = -4 a +24 3) Если D0 = -4 a +240 = 4 a a 2 корня: x 1,2 = -5 4 -a±√(6-a) a-2 -2a±√(24-4a) 2(a-2) = ← → " width="640"

17

Квадратные уравнения с коэффициентом зависимым от параметра

Задача №2. При всех значениях a решить уравнение:

( a -2)x 2 +2 a x+ a +3+0

1) Контрольной точкой параметра a -2=0, является a =2,

при котором уравнение становится линейным.

4x+2+3=0 = 4x=-5 = x=

2) Если a ≠2. D = 4 a 2 -4( a -2)( a +3) = -4 a +24

3) Если D0 = -4 a +240 = 4 a a

2 корня: x 1,2 =

-5

4

-a±√(6-a)

a-2

-2a±√(24-4a)

2(a-2)

=

←

→

a =6 x= 5) Если D a 6 = корней нет -3 -5 2 4 x = x = 2 корня Нет корней 2 корня 6 2 -a±√(6-a) a-2 Ответ: при a a при a6, x= ; при a=2, x= ; при a=6, x= -3 2 -5 4 Ø ← → " width="640"

18

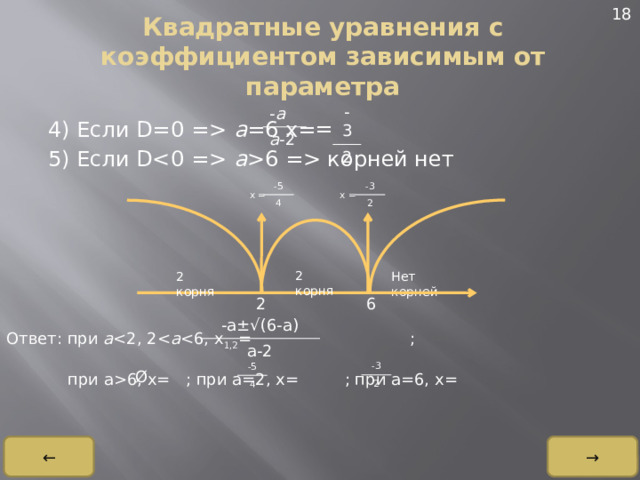
Квадратные уравнения с коэффициентом зависимым от параметра

-3

2

- a

a -2

=

4) Если D=0 = a =6 x=

5) Если D a 6 = корней нет

-3

-5

2

4

x =

x =

2 корня

Нет корней

2 корня

6

2

-a±√(6-a)

a-2

Ответ: при a a

при a6, x= ; при a=2, x= ; при a=6, x=

-3

2

-5

4

Ø

←

→

19

Задачи на применение теоремы Виета

1) ax 2 +bx+c=0,

2) x 2 +px+q=0,

3) Обратная т. Виета:

если x 1 *x 2 = , а x 1 +x 2 = , то эти числа – корня уравнения ax 2 +bx+c=0

4) Если x 1 *x 2 =q, а x 1 +x 2 =-p, то они корни уравнения

x 2 +px+q=0

c

a

x 1 *x 2 =

-b

a

x 1 +x 2 =

x 1 *x 2 =q

x 1 +x 2 =-p

c

-b

a

a

→

←

20

Задачи на применение теоремы Виета

К этому типу относятся задачи в которых

необходимо определить значение параметра, при котором

требуется определить значение параметра при котором

сумма или произведение корней кв. уравнения равны

какому-либо числу; сумма квадратов или кубов корней

принимает наибольшее или наименьшее значения и

т. Виета упрощает это решение.

→

←

0 x 1 *x 2 = 0 При этом оба корня будут «+», если x 1 +x 2 = 0, и отрицательными, если x 1 +x 2 = c a -b a -b a ← → " width="640"

21

Исследование знаков корня

Теорема 1:

Чтобы корни квадратного трехчлена были действительными и имели одинаковые знаки, необходимо и достаточно выполнение следующих условий:

D0

x 1 *x 2 = 0

При этом оба корня будут «+», если x 1 +x 2 = 0,

и отрицательными, если x 1 +x 2 =

c

a

-b

a

-b

a

←

→

0 x 1 *x 2 = При этом «+» корень имеет большую абсолютную величину, если x 1 +x 2 = 0, а если отрицательный большую, то x 1 +x 2 = c a -b a -b a ← → " width="640"

22

Исследование знаков корня

Теорема 2:

Чтобы корни квадратного трехчлена были действительными и имели разные знаки, необходимо и достаточно выполнение следующих условий:

D0

x 1 *x 2 =

При этом «+» корень имеет большую абсолютную

величину, если x 1 +x 2 = 0,

а если отрицательный большую, то x 1 +x 2 =

c

a

-b

a

-b

a

←

→

a=3 (линейное) -6x+18=0 = 6x=18 = x=3 (удовлетовряет условию задачи) 2)a-3≠0 = a≠3 D=4a 2 -4(a-3)6a=-20a 2 +72a=-4a(5a-18) Корни существуют, если D ≥0: -4a(5a-18)≥0 = a(5a-18)≤0 //// 0 18 5 ← → " width="640"

23

Исследование знаков корня

Задача №3: найдите все действительные значения а, при которых корни уравнения (а-3)x 2 -2ax+6a=0 действительные и положительные.

1)a-3=0 = a=3 (линейное)

-6x+18=0 = 6x=18 = x=3 (удовлетовряет условию задачи)

2)a-3≠0 = a≠3

D=4a 2 -4(a-3)6a=-20a 2 +72a=-4a(5a-18)

Корни существуют, если D ≥0:

-4a(5a-18)≥0 = a(5a-18)≤0

////

0

18

5

←

→

0 = по т. Виета x 1 +x 2 = = 0 x 1 *x 2 0 x 1 *x 2 = 0 0 учитывая что 0 но, т.к. при a=3 корень тоже «+», a є [3;3 ] Ответ: a є [3;3 ] 2a 2a a-3 a-3 6a 6a a-3 a-3 a a-3 - + + ////// ////// 3 5 3 0 3 5 → ← " width="640"

24

Исследование знаков корня

Чтобы корни были действительные и положительными нужно, чтобы:

x 1 +x 2 0 = по т. Виета x 1 +x 2 = = 0

x 1 *x 2 0 x 1 *x 2 = 0

0 учитывая что 0

но, т.к. при a=3 корень

тоже «+», a є [3;3 ]

Ответ: a є [3;3 ]

2a

2a

a-3

a-3

6a

6a

a-3

a-3

a

a-3

-

+

+

//////

//////

3

5

3

0

3

5

→

←

M. → ← " width="640"

25

Расположение корней квадратного трехчлена в зависимости от параметра

Пусть f(x)=ax 2 +bx+c, имеет действительные корни

x 1 и x 2 , т.е. D≥0, которые могут быть кратны; а M, A –

какие-нибудь действительные числа, причем AM.

→

←

a=2 = -10x+8=0 = x= , уравнение имеет 1 корень. 2) a≠2: x 2 - + =0 a0 f(2) f(3)4 5 4a a-2 2(a-3) a-2 x 1 x 2 3 2 → ← " width="640"

26

Расположение корней квадратного трехчлена в зависимости от параметра

Задача №4: При каких значениях a один из корней уравнения (a-2)x 2 -2(a+3)x+4a=0 меньше 2, а второй больше.

1) a-2=0 = a=2 = -10x+8=0 = x= , уравнение имеет 1 корень.

2) a≠2:

x 2 - + =0 a0

f(2)

f(3)

4

5

4a

a-2

2(a-3)

a-2

x 1

x 2

3

2

→

←

= f(3)=9- + = 4(a-5)(a-2)36 7 7(a- )(a-2)7a-36 7a-36 6(a+3) 4a a-2 a-2 a-2 a-2 \\\\\\\\ 5 2 //////// 2 36 7 36 7 Ответ: a є (2; ) ← → " width="640"

27

Расположение корней квадратного трехчлена в зависимости от параметра

4a-20

(a+3)

a-2

a-2

4a-20

a-2

4a

a-2

f(2)=2 2 -4 + =

= =

f(3)=9- + =

4(a-5)(a-2)

36

7

7(a- )(a-2)

7a-36

7a-36

6(a+3)

4a

a-2

a-2

a-2

a-2

\\\\\\\\

5

2

////////

2

36

7

36

7

Ответ: a є (2; )

←

→

0 2x0 2x ≠1 08x+a+3=4x 2 x ≠ 04x 2 -8x=a+3 x ≠ 01 1 2 2 a √ 7 2 3 2 3 2 4x 2 -8x-3=a = x 2 -2x- =0 = 1 ±√(1+ )=1± x(в)=8:8=1 y(в)=4-8-3=-7 y(2)=-3 y( )=-6 Ответ: a є {-7;-6;-3} 1 2 1 x 1 2 -3 → ← -6 -7 " width="640"

28

Решение задач с параметром

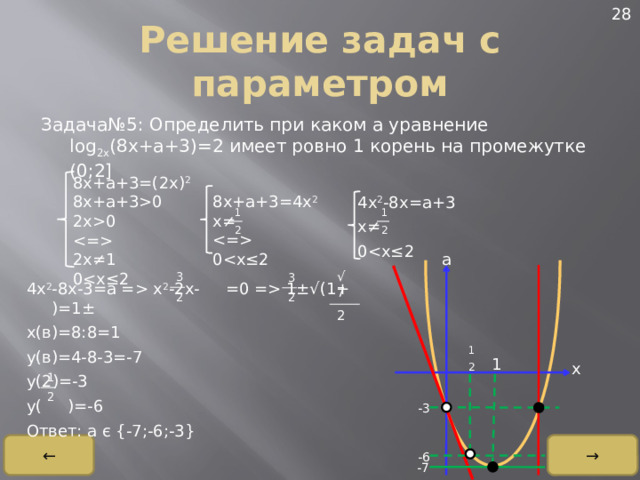
Задача№5: Определить при каком a уравнение log 2x (8x+a+3)=2 имеет ровно 1 корень на промежутке (0;2]

8x+a+3=(2x) 2

8x+a+30

2x0

2x ≠1

0

8x+a+3=4x 2

x ≠

0

4x 2 -8x=a+3

x ≠

0

1

1

2

2

a

√ 7

2

3

2

3

2

4x 2 -8x-3=a = x 2 -2x- =0 = 1 ±√(1+ )=1±

x(в)=8:8=1

y(в)=4-8-3=-7

y(2)=-3

y( )=-6

Ответ: a є {-7;-6;-3}

1

2

1

x

1

2

-3

→

←

-6

-7

=2 a -1 = cos2x=4 a -3; 4 a -3 ≥-1 4 a ≥2 a ≥ 4 a -3≤1 = 4 a ≤4 = a ≤1 Значит при a є [ ;1], x= arccos(4a-3)+ = arccos(4a-3)+∏n а при a є [ ;1], x=Ø Ответ: при a є [ ;1], x= arccos(4a-3)+ = arccos(4a-3)+∏n при a є [ ;1], x=Ø 1+cos2x 2 1 2 1 2 1 2 1 2 2 ∏n 2 1 2 / 1 2 1 2 1 2 2 ∏n 2 1 2 ← → " width="640"

29

Решение задач с параметром

Задача №6: Решить уравнение

cos 2 x=2 a -1 = =2 a -1 = cos2x=4 a -3;

4 a -3 ≥-1 4 a ≥2 a ≥

4 a -3≤1 = 4 a ≤4 = a ≤1

Значит при a є [ ;1], x= arccos(4a-3)+ = arccos(4a-3)+∏n

а при a є [ ;1], x=Ø

Ответ: при a є [ ;1], x= arccos(4a-3)+ = arccos(4a-3)+∏n

при a є [ ;1], x=Ø

1+cos2x

2

1

2

1

2

1

2

1

2

2 ∏n

2

1

2

/

1

2

1

2

1

2

2 ∏n

2

1

2

←

→

1 ОДЗ: log a x(x-2)log a a = 1) a1: x 2 -2x-a0 x 1,2 =1 ±√(1+a) x є ( 1 ±√(1+a);+∞ ) 2) 0 x 2 -2x-a x є (2; 1 ±√(1+a) ) 3) a ≤0 – левая часть не вычислена. Ответ: а1, x є ( 1 ±√(1+a);+∞ ) 0 a ≤0 - левая часть не вычислена. x2 a0 a ≠1 - + + ////// ////// 2 1 -√(1+a) 1 +√(1+a) ////////// 1 +√(1+a) \\\\\\\\\ 2 1 -√(1+a) ← → " width="640"

30

Решение задач с параметром

Задача №7: Решить неравенство

log a x+log a (x-2)1 ОДЗ:

log a x(x-2)log a a =

1) a1:

x 2 -2x-a0

x 1,2 =1 ±√(1+a)

x є ( 1 ±√(1+a);+∞ )

2) 0

x 2 -2x-a

x є (2; 1 ±√(1+a) )

3) a ≤0 – левая часть не вычислена.

Ответ: а1, x є ( 1 ±√(1+a);+∞ )

0

a ≤0 - левая часть не вычислена.

x2

a0

a ≠1

-

+

+

//////

//////

2

1 -√(1+a)

1 +√(1+a)

//////////

1 +√(1+a)

\\\\\\\\\

2

1 -√(1+a)

←

→

a=x 2 ±√(4(x+1) 2 )= x 2 ±2(x+1) a=x 2 +2(x+1) x 2 +2x+2-a=0 x=-1±√(1-2+a) a=x 2 -2(x+1) a-1≥0 x 2 -2x-2-a=0 a≥1 x=-1±√(1+2+a) x 1,2 =-1±√(a-1) a+3≥0 a≥-3 x 3,4 =±√(a+3) ← → " width="640"

31

Решение задач с параметром

Задача №8: Решить уравнение

x 4 -2x 2 (a+2)-8x-4=0

Решаем уравнение как квадратное относительно a

a 2 -2x 2 a+x 4 -4x 2 -8x-4=0

a 2 -2x 2 a+x 4 -4(x+1) 2 =0 = a=x 2 ±√(4(x+1) 2 )= x 2 ±2(x+1)

a=x 2 +2(x+1)

x 2 +2x+2-a=0

x=-1±√(1-2+a)

a=x 2 -2(x+1)

a-1≥0

x 2 -2x-2-a=0

a≥1

x=-1±√(1+2+a)

x 1,2 =-1±√(a-1)

a+3≥0

a≥-3

x 3,4 =±√(a+3)

←

→

32

Решение задач с параметром

.

x 3,4

x 1,2,3,4

x 3,4

x 1,2,3,4

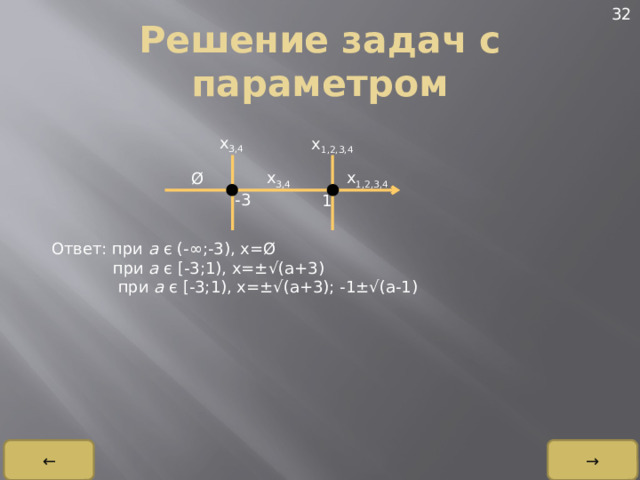
Ø

-3

1

Ответ: при a є (-∞;-3), x=Ø

при a є [-3;1), x=±√(a+3)

при a є [-3;1), x=±√(a+3); -1±√(a-1)

←

→

a-любое. x 1 =a 0≥0 0≤x≤1 x 2 = a є [0;1] (a+1) 2 4 -a 2 ≥0 0≤a+1≤2 = -1≤a≤1 x 2 = a є [- ;1] a+1 2 1 3 → ← " width="640"

33

Решение задач с параметром

Задача №9: Найдите все a при каждом из которых уравнение имеет ровно 1 корень на промежутке[0;1].

√ (x 2 -a 2 )=√(3x 2 -(3a+1)x+a)

x 2 -a 2 = 3x 2 -(3a+1)x+a

x 2 -a 2 ≥0

0≤x≤1

Разложим на множители

x 1 +x 2 =a+

x 1 *x 2 =

(x-a)(x+a)-3(x-a)(x- )=0

1

3

a

3

1

3

a+1

2

x 1 =a = a-любое.

x 1 =a

0≥0

0≤x≤1

x 2 =

a є [0;1]

(a+1) 2

4

-a 2 ≥0

0≤a+1≤2 = -1≤a≤1

x 2 = a є [- ;1]

a+1

2

1

3

→

←

a= = 2a=a+1 = a=1 x 1 = a=1 x 2 = =1 x 1 = a=0 x 2 = = a+1 2 1 2 a+1 2 a+1 2 x 2 = x 1 = a x 2 = a+1 a+1 2 2 x 2 = Нет корней Нет корней 0 1 1 3 - 1 3 - Ответ: a є [ ;0)U{1} → ← " width="640"

34

Решение задач с параметром

a+1

2

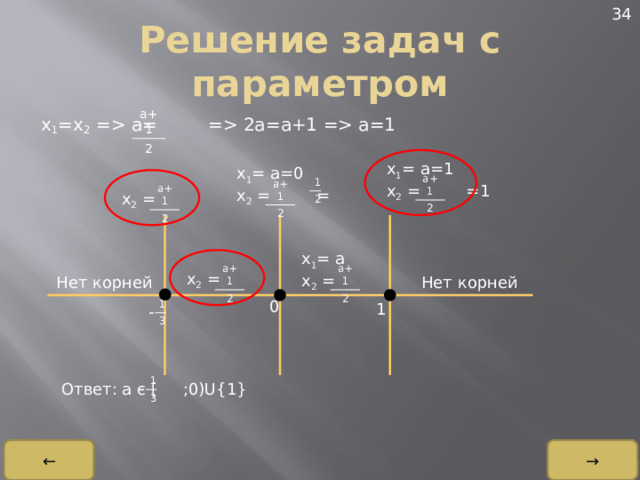
x 1 =x 2 = a= = 2a=a+1 = a=1

x 1 = a=1

x 2 = =1

x 1 = a=0

x 2 = =

a+1

2

1

2

a+1

2

a+1

2

x 2 =

x 1 = a

x 2 =

a+1

a+1

2

2

x 2 =

Нет корней

Нет корней

0

1

1

3

-

1

3

-

Ответ: a є [ ;0)U{1}

→

←

на [1;6] один корень. 4x+1 ≥0 = x≥- [1;6] є ОДЗ a(1) = - 5 √(6.2*1-5.2)- log 5 (4*1+1)=- a(6)= - =- Ответ: a є [- ; - ] 3 5 4 5 - 1 4 7 5 3 5 4 5 8 5 14 5 -6 5 7 5 14 5 1 4 1 6 - - 7 5 - 14 5 ← → " width="640"

35

Решение задач с параметром

Задача №10: Найти a при которых любые решения є [1;6]

3 5 √(6.2x-5.2)+4log 5 (4x+1)+5a=0

Рассмотрим a как функцию x: a=f(x)

Выразим a: a= 5 √(6.2x-5.2)- log 5 (4x+1)

Т.к. на ОДЗ a убывает = на [1;6] один корень. 4x+1 ≥0 = x≥-

[1;6] є ОДЗ

a(1) = - 5 √(6.2*1-5.2)- log 5 (4*1+1)=-

a(6)= - =-

Ответ: a є [- ; - ]

3

5

4

5

-

1

4

7

5

3

5

4

5

8

5

14

5

-6

5

7

5

14

5

1

4

1

6

-

-

7

5

-

14

5

←

→

0 t 2 -(a+3)t+4a-4=0 I D=0 0 II два решения ,одно0; другоеa+3 2 t 1 t 2 0 а) = (a+3) 2 -4(4a-4)=0 a3 t 1 t 2 4a-4 aa 2 6a+9-16a+16= 4a-4=0 = a=1 a=5 t 1 =0 t 2 0; t 1 +t 2 0 4a-4=0 = a=1 a+30 a-3 1+30 (a-5) 2 =0 a-3 Ответ: a ≤1; a=5 ← → " width="640"

36

Решение задач с параметром

Задача №11: При каких a уравнение имеет единственное решение. (исследовать квадратный трехчлен)

4 x -(a+3)2 x +4a-4=0

Заменим 2 x =t t0

t 2 -(a+3)t+4a-4=0

I D=0

0

II два решения ,одно0;

другое

a+3

2

t 1

t 2

0

а) = (a+3) 2 -4(4a-4)=0

a3

t 1 t 2 4a-4 a

a 2 6a+9-16a+16=

4a-4=0 = a=1

a=5

t 1 =0 t 2 0; t 1 +t 2 0

4a-4=0 = a=1

a+30 a-3 1+30

(a-5) 2 =0

a-3

Ответ: a ≤1; a=5

←

→

Оглавление

• Что такое параметр?...............................................................................................2
• Основные типы задач с параметром…………………………………………….3
• Что значит решить уравнение с параметром?......................................................6
• Основные методы решения задач с параметром………………………………..8
• Линейные уравнения с параметром и приводимые к ним……………………..11
• Уравнения с параметром при наличии дополнительных условий…………….14
• Квадратные уравнения с коэффициентом зависимым от параметра………….16
• Задачи на применение теоремы Виета……………………………………….…19
• Исследование знаков корня……………………………………………………...21
• Расположение корней квадратного трехчлена в зависимости от параметра . .25
• Решение задач с параметром…………………………………………………….28

←

→

КОНЕЦ

←