Решение стереометрических задач методом координат

Решение стереометрических задач методом координат

Основные виды задач

Нахождение угла

• между прямыми;
• между прямой и плоскостью;
• между плоскостями;

Нахождение расстояния

• от точки до прямой;
• от точки до плоскости;
• между двумя скрещивающимися прямыми.

Угол между прямыми

№ 1. В кубе ABCDA1B1C1D1 найдите угол между прямыми A 1 C и DE, если E - середина ребра СС 1 .

Ответ:

Угол между прямой и плоскостью

направляющий вектор прямой

вектор нормали к плоскости

Уравнение плоскости: ax+by+cz+d=0

№ 2. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 найдите угол между плоскостью A 1 BC и прямой BC 1 , если AA 1 = 8, AB = 6, BC = 15.

Уравнение плоскости: ax+by+cz+d=0 (1)

B(0;0;0): а0+b0+с0+d=0 , d=0

A 1 (6;0;8):6а+ b0+8с+0=0 , 6a+8c=0

C(0;15;0): 0а+15b+0с+0=0, 15b=0, b=0

6a+8c=0

BA 1 C:

Пусть α – угол

между ВС 1

и плоскостью BA 1 C

Ответ:

Угол между поскостями

№ 3.Основанием прямой призмы ABCDA 1 B 1 C 1 D 1 является ромб с тупым углом B, равным 120°. Все ребра этой призмы равны 10. Точки P и K – середины ребер СС 1 и СD соответственно. а) Докажите, что P K и PB 1 перпендикулярны. б) Найдите угол между плоскостями PKB 1 и С 1 B 1 B.

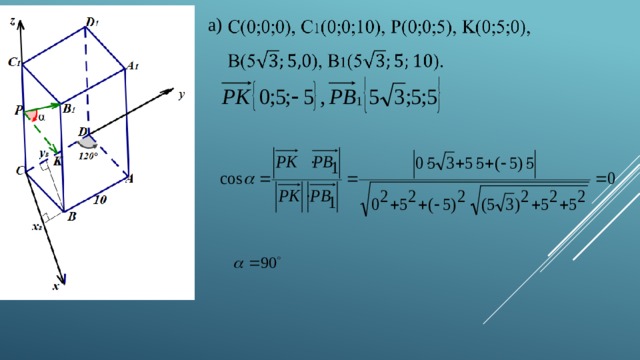
а)

б)

№ 5. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 сторона основания равна 1, а высота равна 6. Найдите угол между прямой B 1 F 1 и плоскостью AF 1 C 1 .

По теореме косинусов=+-2=

=1+1-2 cos=1+1+2 = 3, BF=

Аналогично находим ЕС, ЕС=

(;0;6), ;1;6)