МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО РЕШЕНИЮ №13 ИЗ ЕГЭ ПО МАТЕМАТИКЕ ПРОФИЛЬНОГО УРОВНЯ
Тамбов, 2018
| 1.ТЕОРИЯ | 3 |
| 2.ПРИМЕРЫ ЗАДАЧ | 4 |
| 3.УПРАЖНЕНИЯ ДЛЯ САМОПРОВЕРКИ | 23 |
| 4.ОТВЕТЫ | 24 |
| 5. ИНФАРМАЦИОННЫЕ РЕСУРСЫ | 25 |
СОДЕРЖАНИЕ
ТЕОРИЯ
Прежде чем разбирать решение задач №13 профильного уровня, необходимо вспомнить теорию и основные формулы.
1.1.Нахождение угла между скрещивающимися прямыми
Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку. Градусная мера угла располагается в диапазоне от 0˚ до 90˚.
Данный угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если нам удастся найти координаты направляющих векторов  и
и  то сможем найти угол.
то сможем найти угол.
Точнее, косинус угла по формуле:

1.2.Нахождение угла между плоскостями
Две пересекающиеся плоскости образуют две пары равных между собой двугранных углов:
Величина двугранного угла измеряется величиной соответствующего линейного угла. Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла.
Угол между двумя плоскостями в пространстве равен модулю угла между нормалями к этим плоскостям.
Если мы найдем координаты вектора нормали, то мы воспользовавшись ранее известной формулой косинуса угла между векторами найдем искомый угол.
Вектор нормали к плоскости, заданной уравнением Ах+Ву+Сz+D=0 имеет координаты  {A;B;C}.
{A;B;C}.
После того, как мы нашли координаты векторов нормалей двух плоскостей, угол между двумя пересекающимися плоскостями можно вычислить как
угол между нормалями по формуле: 
1.3. Нахождение угла между прямой и плоскостью
Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.
Итак, для того чтобы найти угол между прямой и плоскостью методом координат нам понадобиться формула: 
или в координатах 


1.4. Нахождение расстояния от точки до плоскости
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние от любой точки с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

ПРИМЕРЫ ЗАДАЧ №13 ПРОФИЛЬНОГО УРОВНЯ
№1 Задание с решу ЕГЭ
Условия: В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 4. Точка L — середина ребра SC. Тангенс угла между прямыми BL и SA равен 
а) Пусть O — центр основания пирамиды. Докажите, что прямые BO и LO перпендикулярны.
б) Найдите площадь поверхности пирамиды.
Решение:
 а) Заметим, что при проецировании на плоскость ABCD точка S проецируется в точку O. Поэтому проекция SC это OC, значит, проекция L тоже лежит на OC и проекция LO тоже прямая OC. Поскольку OC⊥OB как диагонали квадрата, по теореме о трех перпендикулярах LO⊥OB.
а) Заметим, что при проецировании на плоскость ABCD точка S проецируется в точку O. Поэтому проекция SC это OC, значит, проекция L тоже лежит на OC и проекция LO тоже прямая OC. Поскольку OC⊥OB как диагонали квадрата, по теореме о трех перпендикулярах LO⊥OB.
б) Сразу отметим, что  , поэтому
, поэтому . Введем координаты, направив оси из точки O параллельно сторонам квадрата и через вершину S. Обозначая высоту пирамиды за 2h, находим координаты точек B(2, 2, 0), C(-2, 2, 0), A(2, -2, 0), S(0, 0, 2h), L (-1, 1, h). Тогда,
. Введем координаты, направив оси из точки O параллельно сторонам квадрата и через вершину S. Обозначая высоту пирамиды за 2h, находим координаты точек B(2, 2, 0), C(-2, 2, 0), A(2, -2, 0), S(0, 0, 2h), L (-1, 1, h). Тогда,  ={-3,-1, h},
={-3,-1, h}, 
Посчитаем угол между этими векторами:

Решая уравнение, находим  и высота пирамиды SO=2
и высота пирамиды SO=2 .
.
Тогда апофема SH=8 и площадь поверхности  =80
=80
Ответ: 80.
№2 Задание с решу ЕГЭ

Условия:
Основанием прямой треугольной призмы ABC является прямоугольный треугольник ABC с прямым углом C. Прямые
является прямоугольный треугольник ABC с прямым углом C. Прямые  и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что  =AC
=AC
б) Найдите расстояние между прямыми  и
и  , если AC=6, BC=3
, если AC=6, BC=3
Решение:
а) Если  то скалярное произведение векторов
то скалярное произведение векторов  и
и  будет равно 0. Введем систему координат. Пусть
будет равно 0. Введем систему координат. Пусть 
тогда 
получим координаты векторов  и
и 
По условию  =0, а значит, что
=0, а значит, что
 , это возможно, когда
, это возможно, когда  , то есть при a=b или a=-b, однако, ввиду того, что отрицательной длина быть не может, имеем a=b, тогда CA=A
, то есть при a=b или a=-b, однако, ввиду того, что отрицательной длина быть не может, имеем a=b, тогда CA=A что и требовалось доказать.
что и требовалось доказать.
б) Пусть M— середина A , тогда искомое расстояние равно расстоянию от точки M до прямой
, тогда искомое расстояние равно расстоянию от точки M до прямой  поскольку прямая
поскольку прямая  C перпендикулярна
C перпендикулярна  , проведённой к гипотенузе:
, проведённой к гипотенузе:
Это расстояние равно половине высоты прямоугольного треугольника  , проведённой к гипотенузе:
, проведённой к гипотенузе:


№3 Задание с решу ЕГЭ
Условия:
Длина диагонали куба ABCDA1B1C1D1 равна 3. На луче A1C отмечена точка P так, что A1P = 4.
а) Докажите, что PBDC1 — правильный тетраэдр.
б) Найдите длину отрезка AP.
 Решение:
Решение:
а) Введём систему координат как показано на рисунке. Поскольку ребро куба в корень  меньше его диагонали, ребро данного куба равно
меньше его диагонали, ребро данного куба равно  . Тогда точки B, D, C1 имеют координаты (0;
. Тогда точки B, D, C1 имеют координаты (0; ;
; ) , (
) , ( ;
; ;
; ), (
), ( ;
; ;
; ) соответственно.
) соответственно.
Поскольку P лежит на продолжении A1C, отрезок A1P можно рассматривать как диагональ куба с ребром  Тогда точка P имеет координаты (
Тогда точка P имеет координаты (


Найдём расстояние от P до точек D1, B и C1:

Отрезки C1B, DB и DC1 — диагонали граней куба, поэтому по теореме Пифагора  B=DB=D
B=DB=D =
= . Тогда PD=P
. Тогда PD=P =PB=
=PB= B=DB=D
B=DB=D . Значит, все рёбра тетраэдра DBC1P равны, поэтому он правильный.
. Значит, все рёбра тетраэдра DBC1P равны, поэтому он правильный.
б) Координаты точки A:(0;0; ). Раcстояние от точки P до точки A равно
). Раcстояние от точки P до точки A равно

Ответ:
№4 Задание с решу ЕГЭ

Условия:
В правильной шестиугольной призме ABCDEF , все ребра которой равны 1. Найдите расстояние от т. B до прямой
, все ребра которой равны 1. Найдите расстояние от т. B до прямой  .
.
Решение:
Поместим наш шестиугольную призму в систему координат и пропишем координаты точек, которые нам понадобятся
 ,
,  , A(
, A( ;0,5;0), B(
;0,5;0), B(
Теперь докажем перпендикулярность  с помощью скалярного произведения и координаты их векторов соответственно равны
с помощью скалярного произведения и координаты их векторов соответственно равны  и
и  .
.
 , т.к.
, т.к.  .
.
Получается расстояние от точки B до прямой  будет длина отрезка
будет длина отрезка 
Ответ: 2
№5 Задание с решу ЕГЭ
Условия:
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 2, точка M — середина ребра AB, точка O — центр основания пирамиды, точка F делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая MF перпендикулярна прямой SC.
б) Найдите угол между плоскостью MBF и плоскостью ABC.
Решение:
а) Введем координаты с началом в точке A и осями, направленными по AB, по прямой, параллельной OM и по прямой, параллельной OS. Тогда координаты точек будут такими A(0;0;0), B(2;0;0), M(1;0;0), C(1; ;0), O(1;
;0), O(1; ;0), S(1;
;0), S(1; ), F(1;
), F(1; ), где a — высота пирамиды. Найдем ее: 2=SA=
), где a — высота пирамиды. Найдем ее: 2=SA= , откуда a=
, откуда a= ,
, 
Значит,  и
и  . Значит, их скалярное произведение равно
. Значит, их скалярное произведение равно  = 0, поэтому MF⊥ SC.
= 0, поэтому MF⊥ SC.
б) Пусть уравнение плоскости MBF это Ax+By+Cz=0. Подставляя туда координаты точек, находим A+D=0, 2A+D = 0 (откуда A= D = 0) и  Пусть C=
Пусть C= , B=1. Итак, уравнение этой плоскости
, B=1. Итак, уравнение этой плоскости  Найдем по формуле угол между ней и плоскостью z = 0 (ABC).
Найдем по формуле угол между ней и плоскостью z = 0 (ABC).
Получим:

Ответ: 
№6 Задание с alexlarin вар.202
Условия:
В прямоугольном параллелепипеде  АВ=2, АD=1,
АВ=2, АD=1,  =3. Точка К лежит на ребре
=3. Точка К лежит на ребре  так, что СK:
так, что СK: K=5:4. а) Докажите, что прямые
K=5:4. а) Докажите, что прямые  и
и  перпендикулярны. б) Найдите расстояние от точки
перпендикулярны. б) Найдите расстояние от точки  до плоскости
до плоскости  .
.

Решение:
а) Введем прямоугольную систему координат и найдем нужные нам точки  (0;0;3), D(1;2;0) ,
(0;0;3), D(1;2;0) ,  (1;2;3), K(1; 0;
(1;2;3), K(1; 0; )
)
Найдем координаты векторов  и
и  . Их координаты соответственно равны {1; 2; -3} и {0; 2;
. Их координаты соответственно равны {1; 2; -3} и {0; 2; }.
}.

Отсюда следует , что , ч.т.д.
, ч.т.д.
 б) Построим плоскость
б) Построим плоскость 
Зададим уравнение плоскости, найдем координаты три точки искомой плоскости.

Подставляем по очереди координаты точек , D, K в уравнение плоскости.
, D, K в уравнение плоскости.
Для 





Решая данную систему получаем:  , а
, а 
Тогда  ,
, 
Все это подставляем в уравнение плоскости:


Расстояние от точки  до плоскости
до плоскости  найдем по формуле:
найдем по формуле:

Ответ:
№7 Задание с alexlarin вар.210
Условия:
Основанием пирамиды SABC является равносторонний треугольник ABC, длина стороны которого равна 4 .
.
Боковое ребро SC перпендикулярно плоскости основания и имеет длину 2. а) Докажите, что угол между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра BC, а другая проходит через точку С и середину ребра AB равен 45 . б) Найдите расстояние между этими скрещивающимися
. б) Найдите расстояние между этими скрещивающимися
 прямыми.
прямыми.
Решение:
а) AB=BC=AC=4
SC=2;
Найдем из прямоугольного треугольника

S(0;0;2), L( , C(0;0;0), M(0;
, C(0;0;0), M(0;
Найдем координаты вектора  {
{ } и
} и  {
{ }.
}.
 =
= , ч.т.д.
, ч.т.д.

б) Проведем KL∥CM.
Найдем уравнение плоскости SLK.
K( ;
; 0), S(0;0;2), L(
0), S(0;0;2), L(
Для 





Вычитаем из первого уравнения второе и получаем В=0.
Из третьего уравнения следует C= . A=
. A= .
.

d(C,(SLK))=
Ответ:
№8 Задание с alexlarin вар.211
Условия:
 В прямоугольном параллелепипеде
В прямоугольном параллелепипеде на ребре взята точка К так, что
на ребре взята точка К так, что  . а) Докажите, что плоскость АСК делит диагональ
. а) Докажите, что плоскость АСК делит диагональ  в отношении 4:1, считая от точки В. б) Найдите расстояние от точки D до плоскости АСК, если известно, что АВ=4, ВС=3, СС1=2.
в отношении 4:1, считая от точки В. б) Найдите расстояние от точки D до плоскости АСК, если известно, что АВ=4, ВС=3, СС1=2.
Решение:
а) Построим плоскости АСК,  . MK ∥ AC. Получим линию пересечения данных плоскостей - HN. MK ∥
. MK ∥ AC. Получим линию пересечения данных плоскостей - HN. MK ∥  . Тогда
. Тогда  MKD
MKD  .
.
т.О- точка пересечения HN и KB


1) BON
BON .Отсюда следует, что
.Отсюда следует, что  ⇒
⇒
BN=Z ⇒
⇒  , ч.т.д.
, ч.т.д.
б) A(0;4;0), C(3;0;0), K(3;3;2)
1.
2.
3. .
Решая систему получим A=  , B=
, B= , C=
, C= .
.
Уравнение плоскости:  .
.
D(3;4;0). Тогда подставив координаты расстояние h(D,(ACK))= .
.
Ответ: .
.
№9 Задание с alexlarin
Условия:
В прямоугольном параллелепипеде АВ=ВС=4, СС1=8. Точка К середина ребра АВ, точка М середина ребра ВС. Точка Р лежит на ребре DD1 так, что DP:PD1=3:5
а) Докажите, что плоскость КМР перпендикулярна прямой DВ1.
 б) Найдите объем пирамиды, основанием которой является сечение параллелепипеда плоскостью КМР, а вершиной – точка D1.
б) Найдите объем пирамиды, основанием которой является сечение параллелепипеда плоскостью КМР, а вершиной – точка D1.
Решение:
а) Найдем нужные координаты D(0;4;0), M(2;0;0),K(4;2;0), P(0;4;3),D1(0;4;8),B1(4;0;8)
Поместим параллелепипед в систему координат, запишем нужные координаты точек и найдем векторы
Чтобы доказать, что плоскость перпендикулярна к B1D нужно найти вектор нормали к этой плоскости и проверить его коллинеареность к B1D
 Через определитель третьего порядка найдем уравнение плоскости и координаты вектора нормали
Через определитель третьего порядка найдем уравнение плоскости и координаты вектора нормали
6(x-2)-6y+12z=0
6x-6y+12z-12=0



Эти вектора коллинеарны, т.е вектор B1D перпендикулярен плоскости (MKP) .
б) Объем пирамиды находится по формуле V=⅓Sh Сначала найдем площадь сечения SMLDEK =SKMCDА : cosα, где cosα- это угол между плоскостью сечения и его проекцией
SKMCDА = 16-2=14
Найдем угол между плоскостям плоскостями (ABC) и (MKP)
n{1;-1;2}, n1 {0;0;1}

Тогда SMLDEK = (14∙3)/√6 = 7√6
Найдем h, т.е. находим расстояние от точки D1 до плоскости(MPK)

Следовательно VKMLPED1 = ⅓ (70√6/√6)= 70/3
Ответ: 70/3.
 №10 Задание из сборника задач С2
№10 Задание из сборника задач С2
Условия:
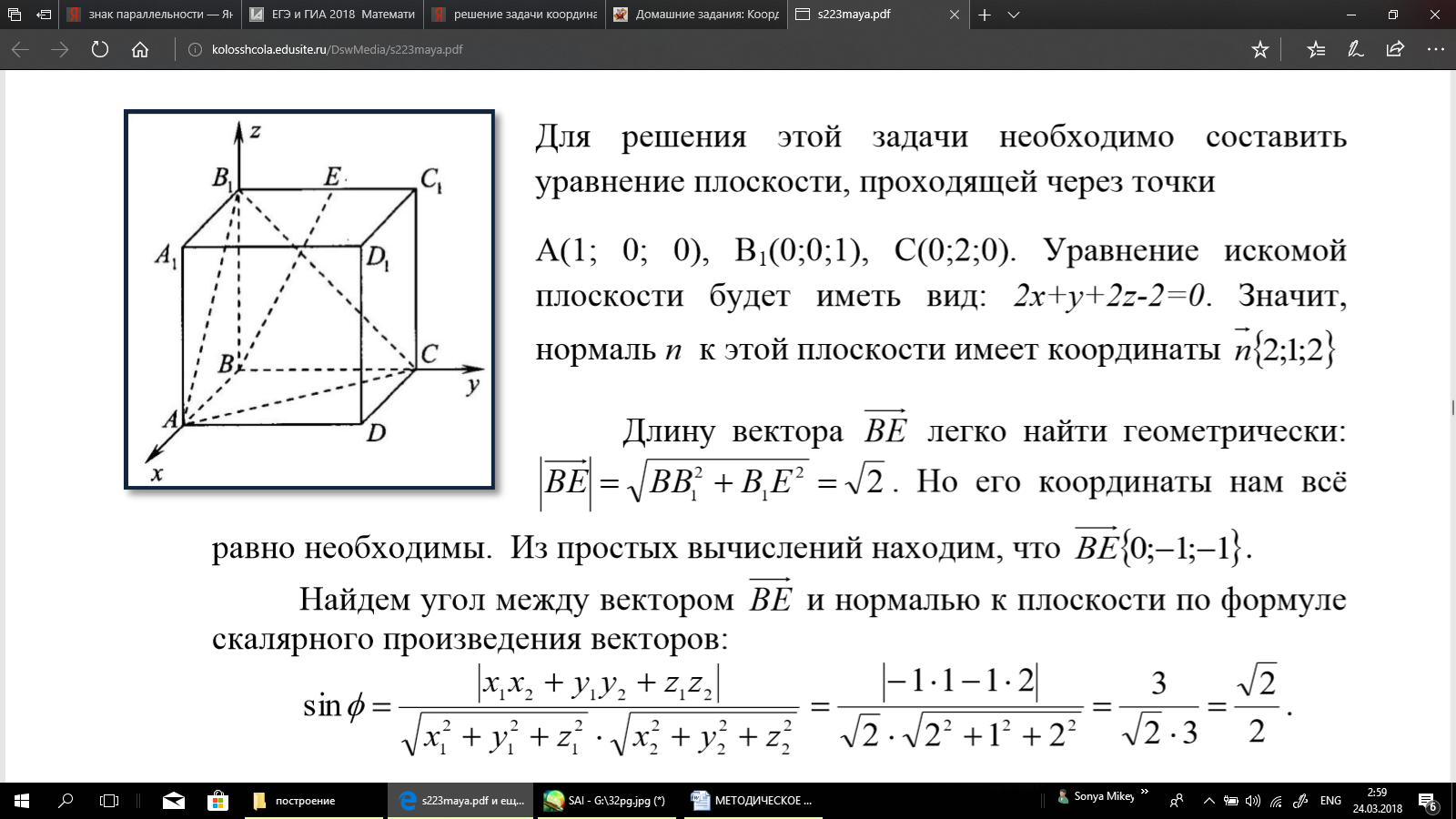
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра АВ и АА1 равны 1, а ребро АD=2. Точка Е – середина ребра В1С1. Найдите угол между прямой ВЕ и плоскостью АВ1С.
Решение:
Для решения этой задачи необходимо составить уравнение плоскости, проходящей через точки
А(1; 0; 0), В1(0;0;1), С(0;2;0). Уравнение искомой плоскости будет иметь вид: 2х+у+2z-2=0. Значит, нормаль n к этой плоскости имеет координаты  {2;1; 2}.
{2;1; 2}.
Длину вектора  легко найти геометрически:
легко найти геометрически: . Но его координаты нам всё равно необходимы. Из простых вычислений находим, что
. Но его координаты нам всё равно необходимы. Из простых вычислений находим, что  . Найдем угол между вектором
. Найдем угол между вектором  и нормалью
и нормалью  к плоскости по формуле скалярного произведения векторов:
к плоскости по формуле скалярного произведения векторов:
Ответ: 45˚
УПРАЖНЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
2. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1.
3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
4. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
5. В основании прямоугольного параллелепипеда ABCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = √10, AD = 3√10. Высота параллелепипеда AA1 = 6 √5. Найдите расстояние от точки A до плоскости A1DB.
ОТВЕТЫ
1.2 √5
2.
3.
4.
5. 2
ИНФОРМАЦИОННЫЕ РЕСУРСЫ
1. Леваков В.В, Методические рекомендации . Решение заданий С2 ЕГЭ по математике координатно-векторным методом. - Саратов МОУ «СОШ № 34 с УИП», 2013
2. Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения- М., 2012
3. Тренировочные варианты с https://reshimvse.com/
4. Тренировочные варианты с http://alexlarin.net/
5.Тренировочные варианты с образовательного портала https://ege.sdamgia.ru/
6. А. Г. Малкова. Подготовка к ЕГЭ по математике. Материалы сайта EGE-Study.ru
7. Федеральный институт педагогических измерений https://fipi.ru/
8. Открытый банк заданий https://mathege.ru







 и
и  то сможем найти угол.
то сможем найти угол. 
 {A;B;C}.
{A;B;C}.






 а) Заметим, что при проецировании на плоскость ABCD точка S проецируется в точку O. Поэтому проекция SC это OC, значит, проекция L тоже лежит на OC и проекция LO тоже прямая OC. Поскольку OC⊥OB как диагонали квадрата, по теореме о трех перпендикулярах LO⊥OB.
а) Заметим, что при проецировании на плоскость ABCD точка S проецируется в точку O. Поэтому проекция SC это OC, значит, проекция L тоже лежит на OC и проекция LO тоже прямая OC. Поскольку OC⊥OB как диагонали квадрата, по теореме о трех перпендикулярах LO⊥OB. , поэтому
, поэтому . Введем координаты, направив оси из точки O параллельно сторонам квадрата и через вершину S. Обозначая высоту пирамиды за 2h, находим координаты точек B(2, 2, 0), C(-2, 2, 0), A(2, -2, 0), S(0, 0, 2h), L (-1, 1, h). Тогда,
. Введем координаты, направив оси из точки O параллельно сторонам квадрата и через вершину S. Обозначая высоту пирамиды за 2h, находим координаты точек B(2, 2, 0), C(-2, 2, 0), A(2, -2, 0), S(0, 0, 2h), L (-1, 1, h). Тогда,  ={-3,-1, h},
={-3,-1, h}, 

 и высота пирамиды SO=2
и высота пирамиды SO=2 .
.  =80
=80
 является прямоугольный треугольник ABC с прямым углом C. Прямые
является прямоугольный треугольник ABC с прямым углом C. Прямые  и
и  перпендикулярны.
перпендикулярны.  =AC
=AC  то скалярное произведение векторов
то скалярное произведение векторов  и
и  будет равно 0. Введем систему координат. Пусть
будет равно 0. Введем систему координат. Пусть  и
и 
 =0, а значит, что
=0, а значит, что  , это возможно, когда
, это возможно, когда  , то есть при a=b или a=-b, однако, ввиду того, что отрицательной длина быть не может, имеем a=b, тогда CA=A
, то есть при a=b или a=-b, однако, ввиду того, что отрицательной длина быть не может, имеем a=b, тогда CA=A что и требовалось доказать.
что и требовалось доказать. , тогда искомое расстояние равно расстоянию от точки M до прямой
, тогда искомое расстояние равно расстоянию от точки M до прямой  поскольку прямая
поскольку прямая  , проведённой к гипотенузе:
, проведённой к гипотенузе:
 Решение:
Решение:  меньше его диагонали, ребро данного куба равно
меньше его диагонали, ребро данного куба равно  ;
; Тогда точка P имеет координаты (
Тогда точка P имеет координаты (


 . Тогда PD=P
. Тогда PD=P


 , все ребра которой равны 1. Найдите расстояние от т. B до прямой
, все ребра которой равны 1. Найдите расстояние от т. B до прямой  .
. ,
,  , A(
, A( ;0,5;0), B(
;0,5;0), B(
 с помощью скалярного произведения и координаты их векторов соответственно равны
с помощью скалярного произведения и координаты их векторов соответственно равны  и
и  .
. , т.к.
, т.к.  .
.
 ;0), S(1;
;0), S(1; ), F(1;
), F(1; ), где a — высота пирамиды. Найдем ее: 2=SA=
), где a — высота пирамиды. Найдем ее: 2=SA= , откуда a=
, откуда a= ,
, 
 и
и  . Значит, их скалярное произведение равно
. Значит, их скалярное произведение равно  = 0, поэтому MF⊥ SC.
= 0, поэтому MF⊥ SC.  Пусть C=
Пусть C= , B=1. Итак, уравнение этой плоскости
, B=1. Итак, уравнение этой плоскости  Найдем по формуле угол между ней и плоскостью z = 0 (ABC).
Найдем по формуле угол между ней и плоскостью z = 0 (ABC).

 АВ=2, АD=1,
АВ=2, АD=1,  =3. Точка К лежит на ребре
=3. Точка К лежит на ребре  так, что СK:
так, что СK: K=5:4. а) Докажите, что прямые
K=5:4. а) Докажите, что прямые  и
и  перпендикулярны. б) Найдите расстояние от точки
перпендикулярны. б) Найдите расстояние от точки  до плоскости
до плоскости  .
.
 (0;0;3), D(1;2;0) ,
(0;0;3), D(1;2;0) ,  )
) и
и  . Их координаты соответственно равны {1; 2; -3} и {0; 2;
. Их координаты соответственно равны {1; 2; -3} и {0; 2; }.
}.
 , ч.т.д.
, ч.т.д. б) Построим плоскость
б) Построим плоскость 







 , а
, а 
 ,
, 




 .
.  . б) Найдите расстояние между этими скрещивающимися
. б) Найдите расстояние между этими скрещивающимися  прямыми.
прямыми. 
 , C(0;0;0), M(0;
, C(0;0;0), M(0;
 {
{ } и
} и  {
{ }.
}. =
= , ч.т.д.
, ч.т.д.
 0), S(0;0;2), L(
0), S(0;0;2), L(




 . A=
. A= .
.


 В прямоугольном параллелепипеде
В прямоугольном параллелепипеде . а) Докажите, что плоскость АСК делит диагональ
. а) Докажите, что плоскость АСК делит диагональ  в отношении 4:1, считая от точки В. б) Найдите расстояние от точки D до плоскости АСК, если известно, что АВ=4, ВС=3, СС1=2.
в отношении 4:1, считая от точки В. б) Найдите расстояние от точки D до плоскости АСК, если известно, что АВ=4, ВС=3, СС1=2.  . MK ∥ AC. Получим линию пересечения данных плоскостей - HN. MK ∥
. MK ∥ AC. Получим линию пересечения данных плоскостей - HN. MK ∥  . Тогда
. Тогда  MKD
MKD  .
. 

 .Отсюда следует, что
.Отсюда следует, что  ⇒
⇒ , ч.т.д.
, ч.т.д.


 , B=
, B= , C=
, C= .
. .
. .
. б) Найдите объем пирамиды, основанием которой является сечение параллелепипеда плоскостью КМР, а вершиной – точка D1.
б) Найдите объем пирамиды, основанием которой является сечение параллелепипеда плоскостью КМР, а вершиной – точка D1.  Через определитель третьего порядка найдем уравнение плоскости и координаты вектора нормали
Через определитель третьего порядка найдем уравнение плоскости и координаты вектора нормали 
 №10 Задание из сборника задач С2
№10 Задание из сборника задач С2 {2;1; 2}.
{2;1; 2}. легко найти геометрически:
легко найти геометрически: . Но его координаты нам всё равно необходимы. Из простых вычислений находим, что
. Но его координаты нам всё равно необходимы. Из простых вычислений находим, что  . Найдем угол между вектором
. Найдем угол между вектором 












