Конспект урока
«Решение треугольников»
«Геометрия является самым
могущественным средством для
изощрения наших умственных
способностей и даёт нам возможность
правильно мыслить и рассуждать»
Г. Галилей.
Цели урока:
-
образовательная - закрепление и углубление знаний учащихся о теоремах синусов и косинусов и их применение к решению треугольников, а также о соотношении между углами треугольника и сторонами, вывод предписания- схемы для решения треугольников, познакомить учащихся с методами решения треугольников.
-
развивающая- продолжить развитие логического мышления через использование ими специальных методов обучения ( анализ, синтез, сравнение, обобщение и конкретизация, аналогия) , активизировать познавательную деятельность учащихся, развивать их инициативу и творчество, развитие подсознательной активности учащихся, формирование учебно-познавательных действий по работе с дополнительной литературой, углубление знаний учащихся о модулировании процессов действительности с помощью аппарата «решение треугольников», умение анализировать и устанавливать связь между элементами темы, развивать критичность мышления
-
воспитательная - воспитать навыки коллективной работы и работы в малых группах , коммуникативных навыков, формирование умений и навыков контроля и самоконтроля личности, организационных умений, прививать учащимся интерес к предмету посредством включения их в решение практических задач, воспитание толерантности.
Используемые технологии:
-
проблемное обучение « Что значит решить треугольник»? Доказать, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.
-
технология уровневой дифференциации обучения.
-
групповые технологии
Обеспечение урока: учебник, инструменты, раздаточный материал, готовые чертежи.
Ход урока
1. Организационный момент.
Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то, как не знать…
Но совсем другое дело —
Очень быстро и умело
Треугольники считать!
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И “по краю” и “внутри”.
Тема урока «Решение треугольников»
(записать в тетради число, тему урока)
Треугольник… Знакомый вам с детства, и начиная с 7 класса, с уроков геометрии, геометрическая фигура, таит в себе немало интересного и загадочного, как Бермудский треугольник, в котором бесследно исчезают корабли и самолеты. В 10-11 классах тоже применяются решения треугольников, поэтому вы должны научиться решать любой треугольник.
2. Проверка теоретических знаний
Тест на определение истинности (ложности) утверждения и правильности формулировок определений
-
В треугольнике против угла в 115° лежит большая сторона. (+)
-
В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60°.(+)
-
Существует треугольник со сторонами: 4 см, 14 см, 3 см. (-)
-
Прямоугольный равнобедренный треугольник имеет равные катеты. (+)
-
Синус острого угла прямоугольного треугольника больше 1. (-)
-
В равностороннем треугольнике все биссектрисы равны. (+)
-
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. (-)
-
Существует треугольник с двумя тупыми углами. (-)
-
В прямоугольном треугольнике сумма острых углов равна 90°.(+)
-
Если сумма двух углов меньше 90°, то треугольник тупоугольный. (+)
ОТВЕТ: + + - + - + - - + +
- У вас на парте лежит листочек с оценочной картой. Проверьте свои ответы и поставьте себе оценку в эту карту.
3. Отработка формул
Найди ошибку (написать на доске)
-
a = b² + c² – 2bc cos 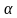
-
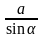 =
= 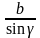 =
= 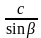
-
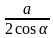 = R
= R
-
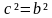 + a² - abcos
+ a² - abcos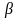
-
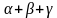 = 360
= 360
-
a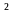 = b² + c² – 2bc
= b² + c² – 2bc 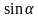
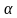
4. Решение задачи с практическим содержанием.
Футбольный мяч находится в точке А футбольного поля на расстояниях 23 м и 24 м от оснований В и стоек ворот. Футболист направляет мяч в ворота. Найдите угол A попадания мяча в ворота, если ширина ворот равна 7 м.
О твет: 17
твет: 17
5. Работа в парах (ПРОВЕРКА!!!)
Соотнесите высказывание с его названием или формулой
| Высказывание | Название, формулы |
| 1. Треугольник называется равнобедренным, если две его стороны равны. 2. Стороны треугольника пропорциональны синусам противолежащих углов. 3. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны. 4. В равнобедренном треугольнике углы при основании равны. 5. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. 6. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 7. Средняя линия треугольника параллельна стороне треугольника и равна ее половине. 8. Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду 9. Внешний угол треугольника – это угол, смежный с углом треугольника. 10.Радиус окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному произведению синуса противолежащего угла | а) определение равных треугольников; б) признак равенства треугольников; в) определение средней линии треугольника; г) свойство средней линии треугольника; д) определение равнобедренного треугольника; е) свойство равнобедренного треугольника; ж) теорема синусов; з) теорема косинусов; и) теорема Пифагора; к) лемма л) 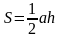 ; ; м) R =  н) 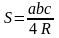 ; ; о) определение внешнего угла треугольника; п) свойство внешнего угла треугольника; р) определение подобных треугольников;
|
6. Физминутка
7. Решение задач (работа в группах)
Решить треугольник и найти его периметр
1 группа: a = 5, 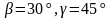
2 группа: а = 20, 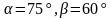
3 группа: b= 12, 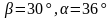
4 группа: а = 12, b = 8, 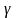 = 60
= 60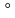
5 группа: b = 18, c = 22, 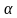 = 76
= 76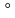
6 группа: a = 8, c = 6, 
1 -11,3 (МО); 2 -52,5(Л) 3 – 48,4 (О), 4 – 32,6(Д), 5 – 64,9(ЦЫ), 6 – 27,2(!!!)
Получилось слово «МОЛОДЦЫ!!!»
8. Домашнее задание
Вычислите неизвестные элементы треугольника АВС:
| № | а | b | c |  A A
|  B B
|  C C
|
| 1 | 3 | | 2 | | 60° | |
| 2 | | 3 | 4 | 135° | | |
| 3 | 2,4 | 1,3 | | | | 28° |
| 4 | 5 | | | | 30° | 45° |
| 5 | 2 | 4 | | 60° | | |
9. Рефлексия
Ребята по одному высказываются одним предложением, выбирая начало фразы на экране
-
Сегодня я узнал …..
-
Было интересно…
-
Было трудно….
-
Я понял, что…
-
Теперь я могу…
-
Я почувствовал, что…
-
Я приобрел…
-
Я научился…
-
У меня получилось…
-
Я смог…
-
Мне захотелось...
-
Я попробую…
9. Подведение итогов урока.






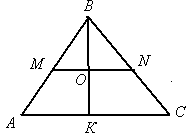
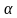
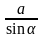 =
= 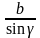 =
= 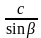
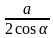 = R
= R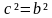 + a² - abcos
+ a² - abcos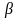
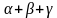 = 360
= 360
 = b² + c² – 2bc
= b² + c² – 2bc 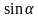
 твет: 17
твет: 17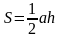 ;
;
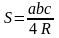 ;
;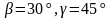
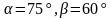
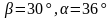
 = 60
= 60



















