Решение уравнений в целых числах

Решение уравнений в целых числах.

Уланова Т.Н.

Учитель математики

«Лицей №21»

Г.Дзержинск Нижегородской области.

Линейное уравнение ax+by=c

- Если НОД(a,b)=1, то уравнение имеет хотя бы одно решение:

где (x 0 ,y 0 ) - некоторое частное целочисленное

решение для t ∊Z

- Если НОД(a,b) ≠ 1, то уравнение не имеет целочисленных решений.

Пример1 : Решить в целых числах уравнение:

7x+9y=32

НОД(7 ; 9)=1, целочисленное решение (2;2), значит

x=2+9t, y=2-7t, t ∊Z .

Ответ: x=2+9t, y=2-7t, t ∊Z .

Пример2 : Решить в целых числах уравнение:

3x-4y=1

НОД(3 ; 4)=1, целочисленное решение (3;2), значит

x=3-4t, y=2-3t, t ∊Z .

Ответ: x=3-4t, y=2-3t, t ∊Z .

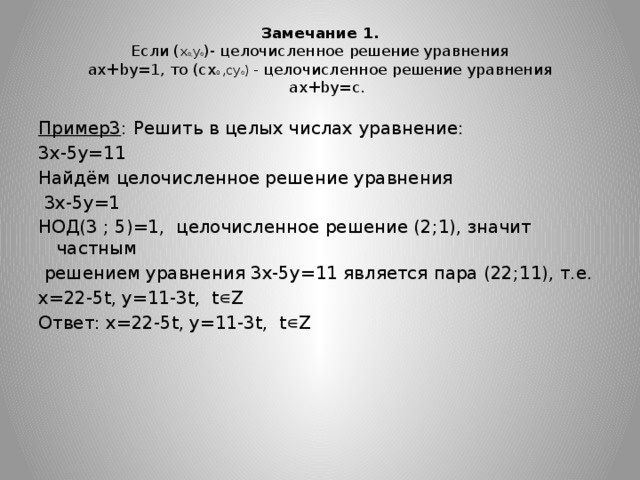
Замечание 1. Если ( x 0, y 0 )- целочисленное решение уравнения ax+by=1, то (cx 0 ,cy 0 ) - целочисленное решение уравнения ax+by=c.

Пример3 : Решить в целых числах уравнение:

3x-5y=11

Найдём целочисленное решение уравнения

3x-5y=1

НОД(3 ; 5)=1, целочисленное решение (2;1), значит частным

решением уравнения 3x-5y=11 является пара (22;11), т.е.

x=22-5t, y=11-3t, t ∊Z

Ответ: x=22-5t, y=11-3t, t ∊Z

Замечание 2. Если трудно подобрать частное решение, то можно применить алгоритм Евклида.

Пример 4 : Решить в целых числах уравнение:

-23x+79y=1

НОД(23 ; 79)=1, значит существует целочисленное решение.

79=23 ⋅ 3+10

23=10 ⋅ 2+3

10=3 ⋅ 3 + 1

1=10-3 ⋅ 3=10-3 ⋅( 23-10 ⋅ 2)=-3 ⋅ 23+10 ⋅ 7=-3 ⋅ 23+7 ⋅( 79-23 ⋅ 3)=

=7 ⋅ 79-24 ⋅ 23

-23 ⋅ 24 + 79 ⋅ 7=1, значит частным решением данного уравнения является пара чисел (24;7), т.е. решение

x=24+79t, y=7+23t, t ∊Z .

Ответ: x=24+79t, y=7+23t ,t ∊Z .

Метод разложения на множители. Пример 5 : Решить в целых числах уравнение: x+xy-3y=5 x-3+y(x-3)=5-3 (x-3)(y+1)=2 = = = Ответ:(1;-2),(2;-3),(4;1),(5;0). " width="640"

=

Метод разложения на множители.

Пример 5 : Решить в целых числах уравнение:

x+xy-3y=5

x-3+y(x-3)=5-3

(x-3)(y+1)=2

=

=

= Ответ:(1;-2),(2;-3),(4;1),(5;0).

0 = Ответ: (5;6),(-6;-5),(-3;4),(-4;3). " width="640"

Пример 6 : Решить в целых числах уравнение:

+91 =

- = 91

= 91 ,91=7 ⋅ 13=1 ⋅ 91

0 =

Ответ: (5;6),(-6;-5),(-3;4),(-4;3).

Соображения делимости.

Пример 7 : Решить в целых числах уравнение:

Рассмотрим остатки от деления на 4 чисел вида .

1) Если х и у чётные, то делится на 4.

2) Если одно из чисел чётное, а второе - нечётное, то остаток от деления на 4 выражения равен 1, т.к.

3) Если оба числа нечётные, то остаток от деления

На 4 равен 2.

Рассмотрим правую часть данного уравнения

4z-1=4z-4+3=4(z-1)+3 , т.е. при делении на 4 правая часть

имеет остаток 3.

Т. к. левая часть и правая часть имеют разные остатки , то

Ни при каких х , у , z уравнение решений не имеет.

Ответ: решений нет.

- Этот метод часто используется для доказательства того, что уравнение не имеет решений в целых числах.

Пример 8 : Решить в целых числах уравнение:

+3=7у

Остаток от деления на7

Т.к. 7у = делится на 7, то

х=7k+2 или х=7k+5, где k ∊Z.

При х=7k+2

7у=

у=

При х=7k+5

7у=

у=

Ответ: , , .

0

1

0

2

3

1

3

4

4

4

0

2

5

2

6

5

5

4

1

0

4

Метод решения уравнения относительно одного из неизвестных.

Пример 9 : Решить в целых числах уравнение:

х+у =ху

у=ху-х , у=х(у-1)

Рассмотрим 2 случая:

• Если у=1, то уравнение не имеет решений, т. к. х(1-1)=0 1 ≠ 0.
• Если у ≠ 1, то , ,

Последнее равенство имеет целые решения, если у-1= 1

т.е. у=0, у=2. Ответ: (0;0), (2;2).

Пример 10 : Решить в целых числах уравнение:

3ху+14х+17у+71=0

т.к х ∊Z

Т.к.(3у+14) ∊ Z, то (3х+17) ⋮ 25.

Следовательно, (3х+17) :±1, ±5, ±25.

Поэтому х=-4, х=-6 , х=-14 .Соответственно у=-3, у=-13. у=-5.

Ответ: (-4;-3), (-6;-13), (-14;-5).

Другие примеры.

Пример 11 : Решить в натуральных числах уравнение:

х!+у!=z!

Заметим, что z 2, ⟹ х z, у z ⟹ х z-1 , у z-1 ⟹

х!+у! 2(z-1)! ⟹ z! 2(z-1)! ⟹ z(z-1)! 2(z-1)! ⟹ z 2.

Итак z =2, тогда х!+у! =2, т.е. х=у=1.

Ответ: х=1, у=1, z =2.

Пример 12 : Решить в натуральных числах уравнение:

и по условию

Проверка

Ответ: