§ 3. Решение задач линейного программирования в Microsoft Excel
Для решения задач оптимизации в MsExcel используют надстройку «Поиск решения», которая вызывается из пункта главного меню «Данные» (рис. 1).
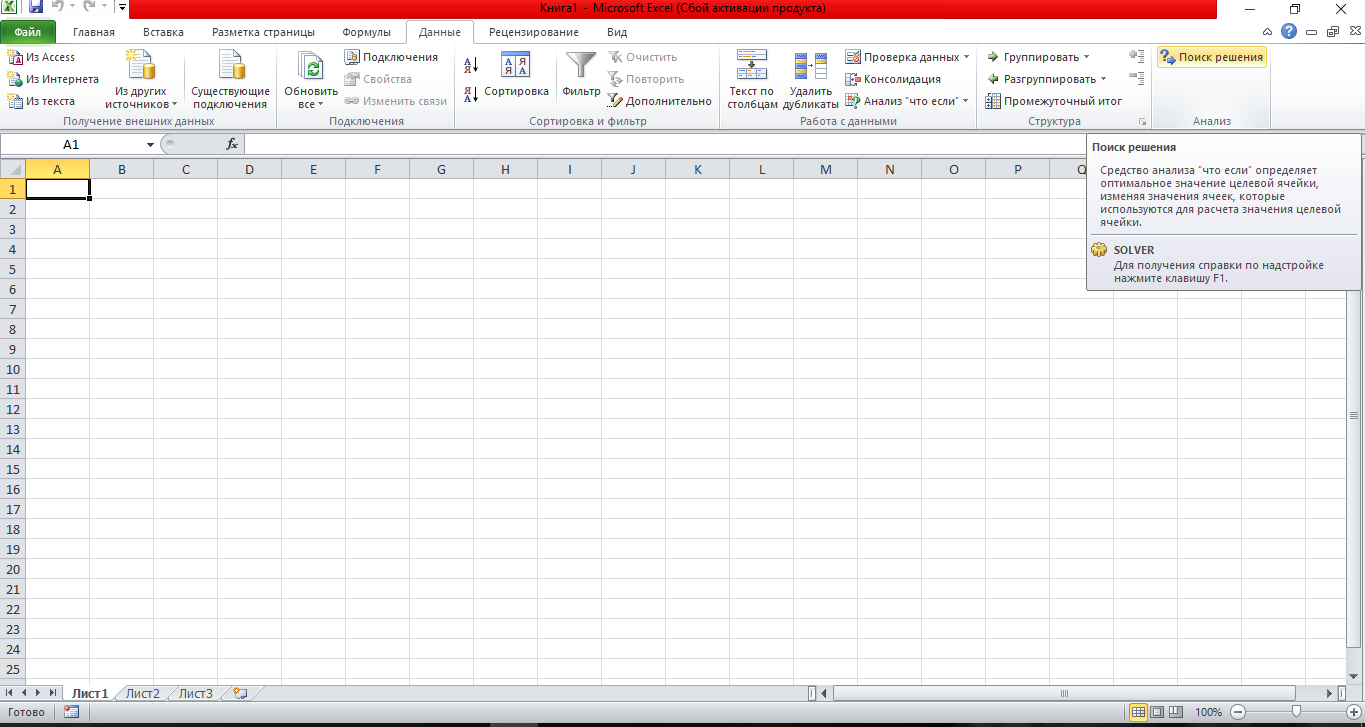
Рис. 1 Вызов надстройки «Поиск решения».
Если в версии Excel, установленной на вашем компьютере, отсутствует данный подпункт, необходимо вызвать пункт меню «Надстройки» и в предложенном списке дополнительных модулей выбрать «Поиск решения»
(рис. 2).
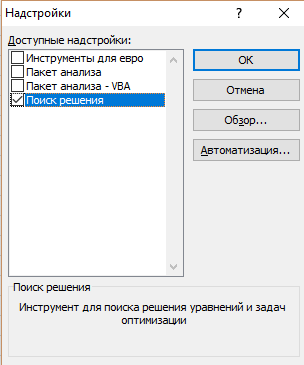
Рис. 2. Вызов пункта меню «Надстройки»
Пример 1.
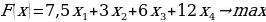
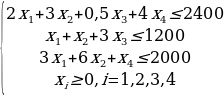
Cоставим шаблон в редакторе Exсel, как показано на рисунке 3.
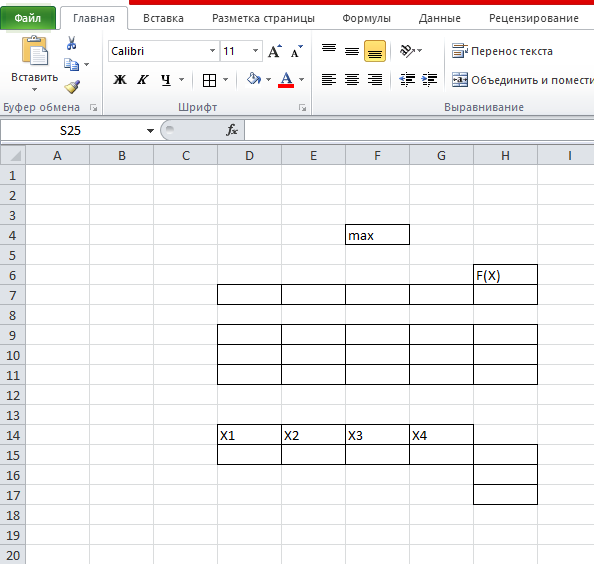
Рис. 3. Шаблон
Занесем в данную задачу числовую информацию (рис. 4.).
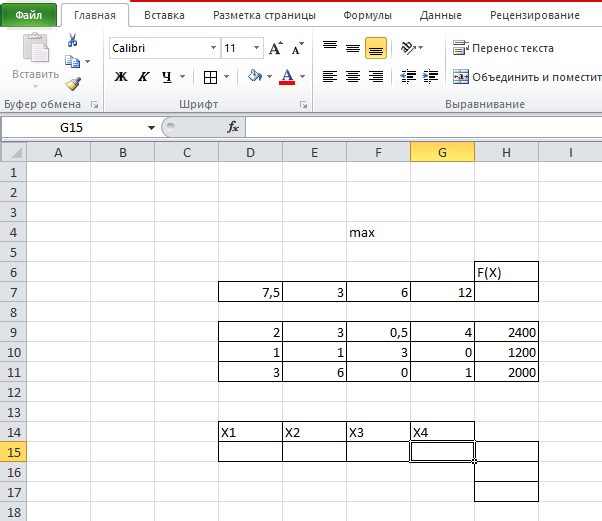
Рис. 4. Ввод числовой информации
В выделенные пустые ячейки (значение целевой функции и Н14 – Н16 – рис. 4) необходимо занести формулы, отображающие связи и отношения между числами на рабочем столе. Ячейки D15 – G15 называются в Excel изменяемыми, т.е. изменяя их, «Поиск решения» будет находить оптимальное значение целевой функции. Значения, которые первоначально вводят в эти ячейки, обычно нули ( незаполненные ячейки расценивается по умолчанию как содержащие нулевые значения).
Введем необходимые формулы. В рассматриваемой математической модели целевая функция представляет собой произведение вектора коэффициентов на вектор неизвестных. Действительно, выражение 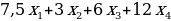 можно рассматривать как произведение вектора (7,5; 3; 6; 12) на вектор (x1, x2, x3, x4).
можно рассматривать как произведение вектора (7,5; 3; 6; 12) на вектор (x1, x2, x3, x4).
В Excel существует функция СУММПРОИЗВ, которая позволяет найти скалярное произведение векторов. В ячейку Н7 необходимо вызвать данную функцию, а в качестве перемножаемых векторов задать адреса ячеек, содержащих коэффициенты уравнений (в данном примере, это D7:G7) и ячеек, в которые в результате решения будут помещены значения x1, x2, x3, x4 (ячейки D15:G15) (рис. 5).
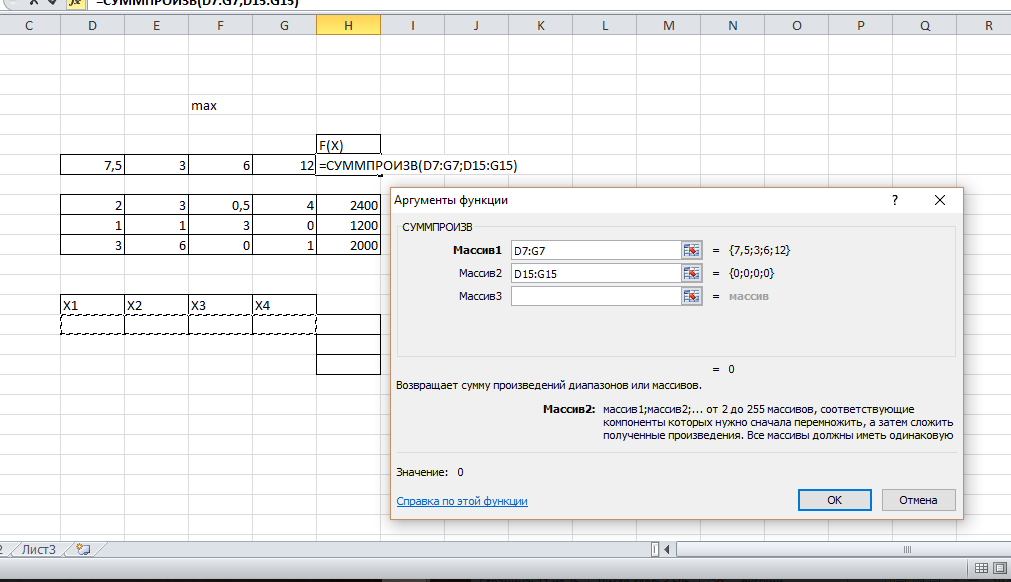
Рис. 5. Заполнение полей окна «Аргументы функции» для целевой функции.
В ячейке, отведенной для формулы левой части первого ограничения (Н15), вызовем функцию СУММПРОИЗВ. В качестве адресов перемножаемых векторов занесем адрес строки коэффициентов D9;G9 и адрес значений переменных D15;G15 (рис. 6).
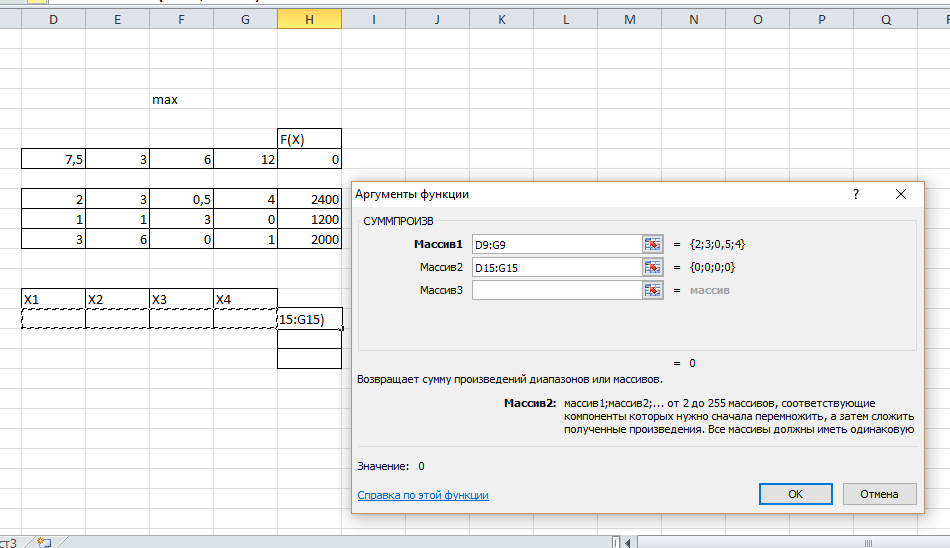
Рис. 6. Заполнение полей окна «Аргументы функции» левой части первого ограничения модели.
В две оставшиеся ячейки графы вводим аналогичные формулы, используя соответствующую строку матрицы затрат. Фрагмент экрана с введенными формулами показан на рис. 7.
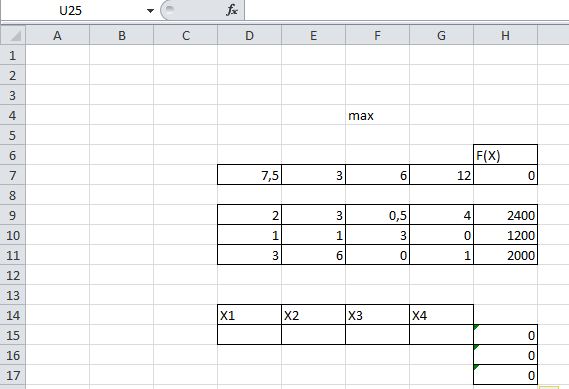
Рис. 7. Фрагмент экрана с введенными формулами
В меню «Данные» выбираем «Поиск решения». В появившемся окне задаем следующую информацию:
-
в качестве целевой ячейки устанавливаем адрес ячейки для значения целевой функции Н7;
-
«флажок» устанавливаем на вариант «максимальному значению», так как в данном примере целевая функция стремится к максимуму;
-
в качестве изменяемых ячеек заносится адрес строки значений переменных D15:F15;
-
справа от окна, предназначенного для занесения ограничений, нажимаем кнопку «Добавить», появится форма для занесения ограничения (рис. 8);
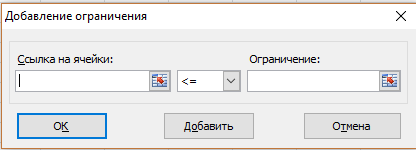
Рис. 8. Форма для занесения ограничений
-
в левой части формы «Ссылка на ячейку» заносится адрес формулы для левой части первого ограничения Н15, выбирается требуемый знак неравенства (в нашем случае
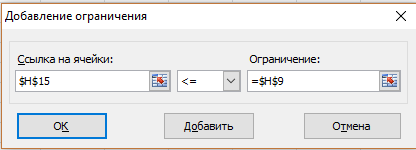
Рис. 9. Заполнение окна «добавить ограничения»
-
аналогично заносятся все ограничения задачи, после чего нажимается кнопка «ОК». Далее нужно установить «флажки» «Поиск решение линейных задач симплекс – методом» и «Сделать переменные без ограничений неотрицательными», так как условие задачи требует неотрицательности переменных (рис. 10).
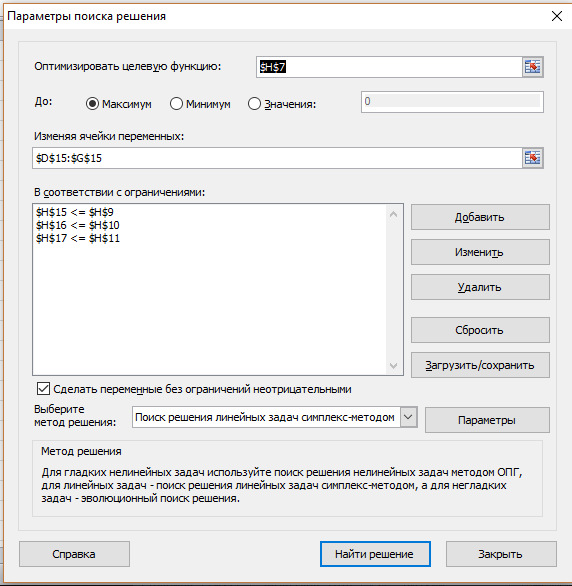
Рис. 10. Окно «Поиск решения» с занесенной информацией
Затем следует нажать кнопку «Найти решение», после чего появится окно результата поиска решения (рис. 11).
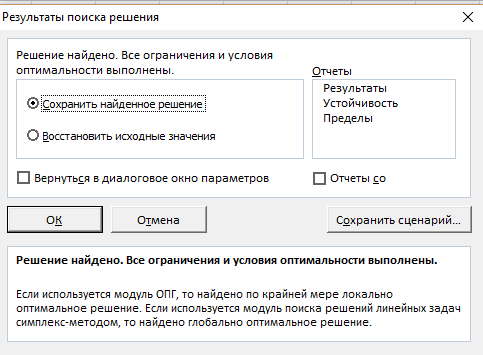
Рис. 11. Окно «Результата поиска решения»
Если в результате всех действий получено окно с сообщением «Решение найдено», то возможно получить три типа отчета, которые нужны при анализе модели на чувствительность. В данном примере достаточно сохранить найденное решение, нажав кнопку «ОК». Получено решение задачи (рис. 12).
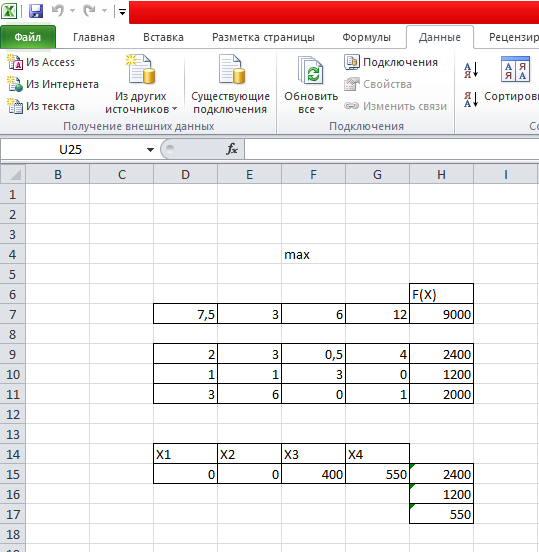
Рис. 12. Результаты решение ЗЛП
Если в результате решения задачи выдано окно с сообщением о невозможности нахождения решения, то это означает, что при оформлении задачи была допущена ошибка. [Мастяева И.Н., 2016]









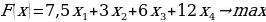
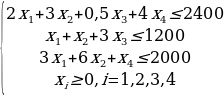


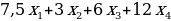 можно рассматривать как произведение вектора (7,5; 3; 6; 12) на вектор (x1, x2, x3, x4).
можно рассматривать как произведение вектора (7,5; 3; 6; 12) на вектор (x1, x2, x3, x4).


























