Решение задач на построение сечений тетраэдра

Решение задач на построение сечений тетраэдра

Учитель математики

Инсаркин С.Б.

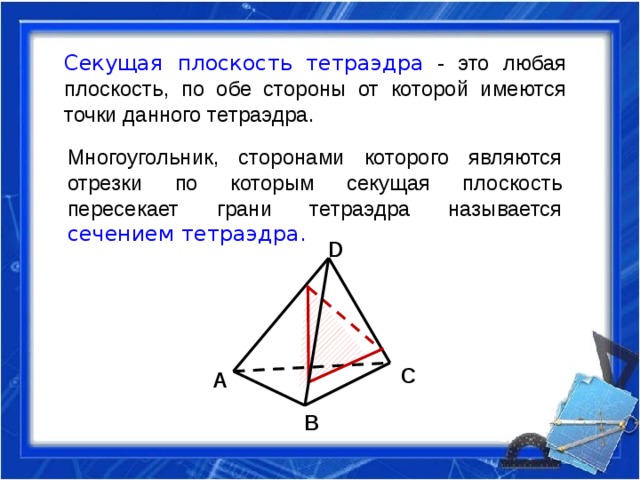
Секущая плоскость тетраэдра - это любая плоскость, по обе стороны от которой имеются точки данного тетраэдра.

Многоугольник, сторонами которого являются отрезки по которым секущая плоскость пересекает грани тетраэдра называется сечением тетраэдра.

D

C

А

B

D

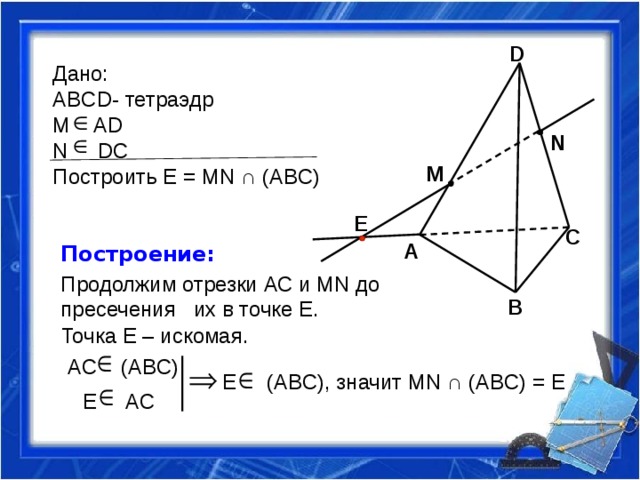
Дано:

ABCD- тетраэдр

M AD

N DC

Построить Е = MN ∩ (AВC)

N

M

E

C

A

Построение:

Продолжим отрезки АС и MN до пресечения их в точке Е.

B

Точка Е – искомая.

AC (ABC)

E (ABC), значит MN ∩ (AВC) = Е

E AC

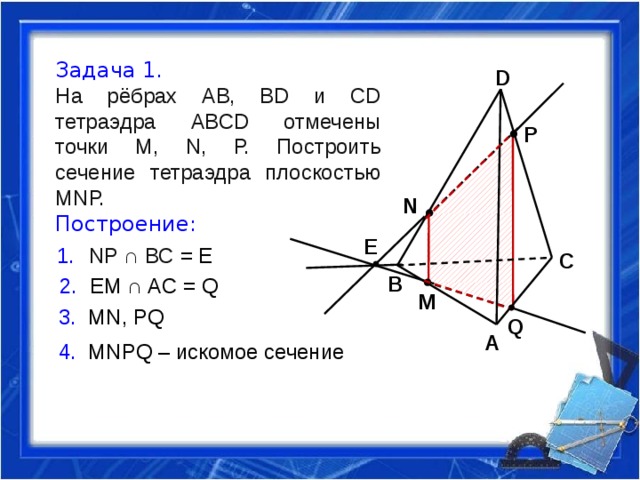
Задача 1.

На рёбрах АВ, ВD и СD тетраэдра АВСD отмечены точки М, N, Р. Построить сечение тетраэдра плоскостью МNР.

Построение:

D

P

N

E

• NР ∩ ВС = Е

C

B

• EM ∩ AC = Q

M

3. MN, PQ

Q

A

4. MNPQ – искомое сечение

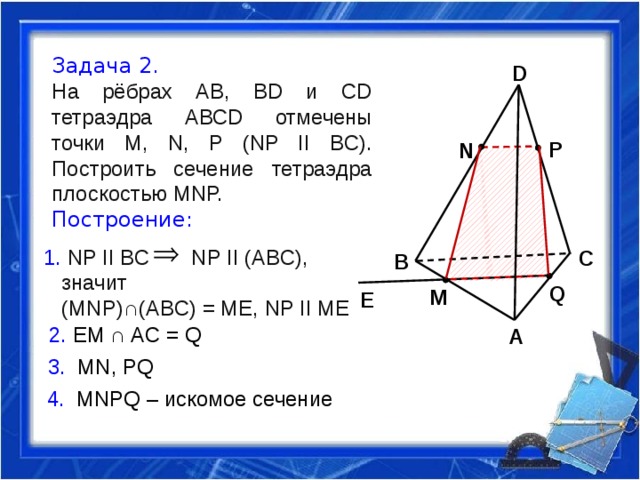
Задача 2.

На рёбрах АВ, ВD и СD тетраэдра АВСD отмечены точки М, N, Р (NP II BC). Построить сечение тетраэдра плоскостью МNР.

Построение:

D

P

N

1. NP II BC NP II (ABC),

значит

(MNP)∩(ABC) = ME, NP II ME

C

B

Q

M

E

2. EM ∩ AC = Q

A

3. MN, PQ

4. MNPQ – искомое сечение

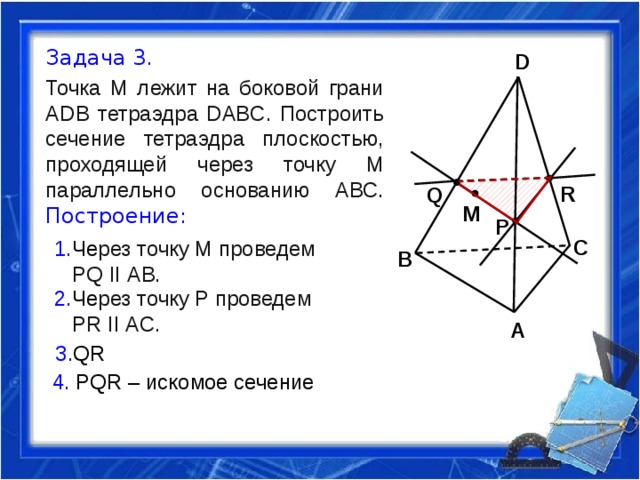
Задача 3.

Точка М лежит на боковой грани ADB тетраэдра DABC. Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно основанию АВС. Построение:

D

R

Q

M

P

C

1. Че рез точку М проведем

PQ II АВ.

B

2. Че рез точку P проведем

PR II АC.

A

3. QR

4. PQR – искомое сечение

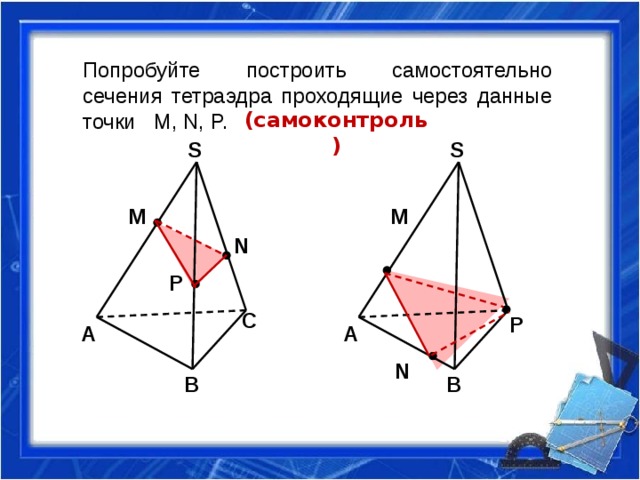
Попробуйте построить самостоятельно сечения тетраэдра проходящие через данные точки M, N, P.

(самоконтроль)

S

S

M

M

N

P

C

P

A

A

N

B

B

Практическая работа «Построение сечений тетраэдра на готовых чертежах»

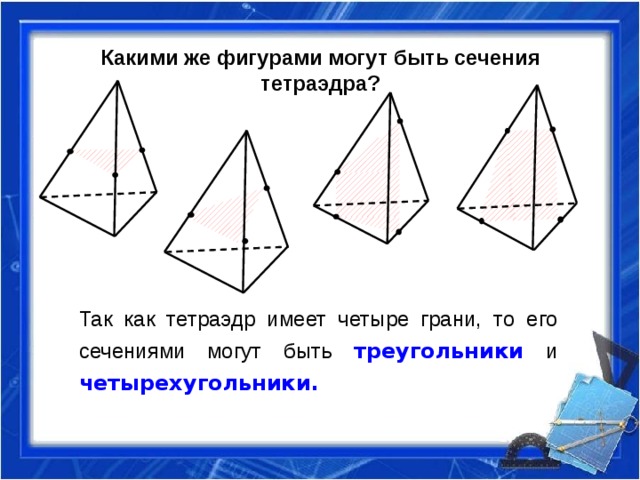
Какими же фигурами могут быть сечения тетраэдра?

Так как тетраэдр имеет четыре грани, то его сечениями могут быть треугольники и четырехугольники.