Решение задач на применение признаков подобия треугольников.

Конспект урока геометрии

Класс: 8

Тема: Решение задач на применение признаков подобия треугольников.

Ход урока

1. Организационный момент

- Здравствуйте! Будем знакомы, меня зовут Анастасия Владимировна. Рада вас всех видеть на уроке геометрии. Проверьте готовность к уроку.

2. Определение темы и цели урока

- Вспомним, какие новые понятия, утверждения, теоремы вы изучали на последних предыдущих уроках? (подобные треугольники, пропорциональные отрезки, коэффициент подобия, отношение площадей, признаки подобия треугольников)

- То есть вы уже готовы прямо сейчас решать контрольную работу по данной теме? (нет)

- Почему? (не до конца усвоена тема, мало решали задач на применения признаков подобия и т.д.)

- На ваших столах листочки. Дерево условно назовем темой «Подобные треугольники», отметьте на нем себя, где вы сейчас находитесь, на каком уровне освоили данную тему. (1 слайд)

- Значит, какую цель поставите перед собой на уроке? (тренировка, решать задачи, применение признаков подобия при решении задач и т.д.)

- Отлично, то есть сегодня на уроке мы будем применять признаки подобия при решении задач.

3. Актуализация знаний

3.1 Теоретический опрос

- Для решения задач нам понадобятся знание некоторых определений, изученных ранее. Вспомните их: (2 слайд)

- Какие треугольники называются подобными? (Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого).

- Определите сходственные стороны подобных треугольников, назовите их (3 слайд)

- Что такое коэффициент подобия? (число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия).

- Чему равно отношение площадей двух подобных треугольников? (Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия).

- Цель нашего урока предполагает решения задач на применение признаков подобия, нам необходимо знать эти признаки.

- Сколько признаков подобия существует? Вспомним и назовем все три признака (ответы детей).

- Это те теоретические знания, которые нам сегодня пригодятся при решении задач.

- Откройте тетради, запишите число, тему урока: Решение задач на применение признаков подобия треугольников. (4 слайд)

3.2 Решение задач на готовых чертежах

- Задание: решение задач по готовым чертежам. Чертежи представлены на слайде, пронумерованы, каждому чертежу соответствует задание. В тетради вы записываете только краткие ответы таким образом: 1) назвать подобные треугольники; 2) указать признак подобия; 3) найти неизвестные элементы.

- На решение каждой задачи отводится 2 минуты. Обращаю ваше внимание, на установление правильного соответствия между сторонами подобных треугольников. Приступаем к решению.

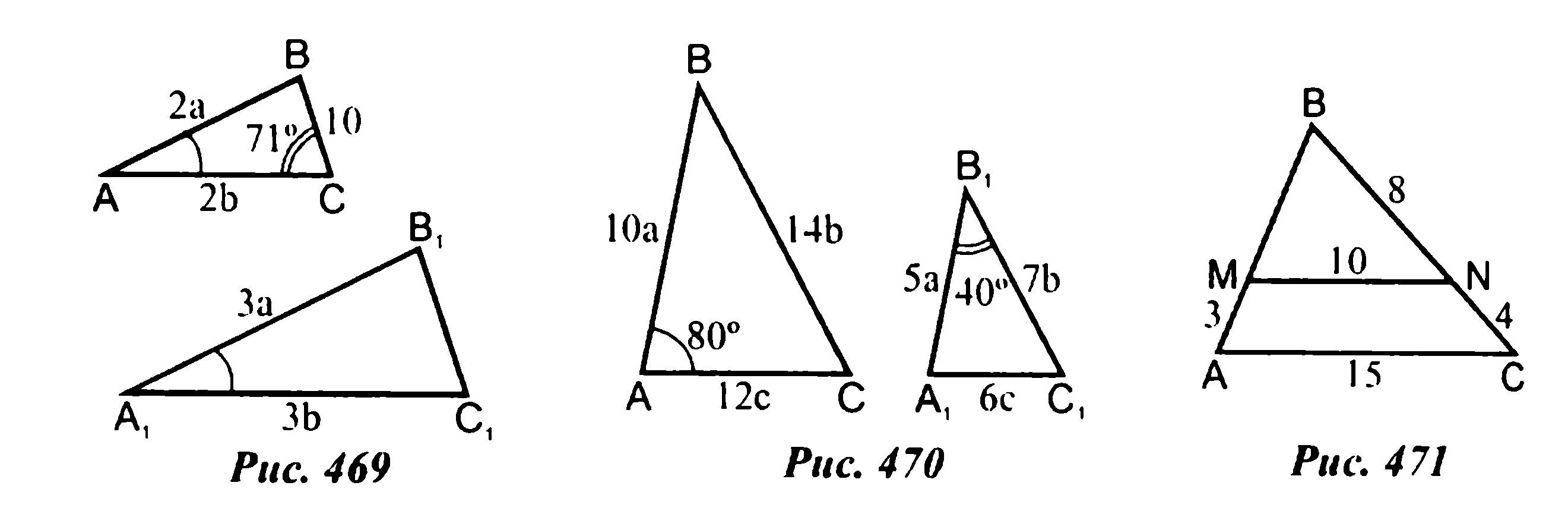
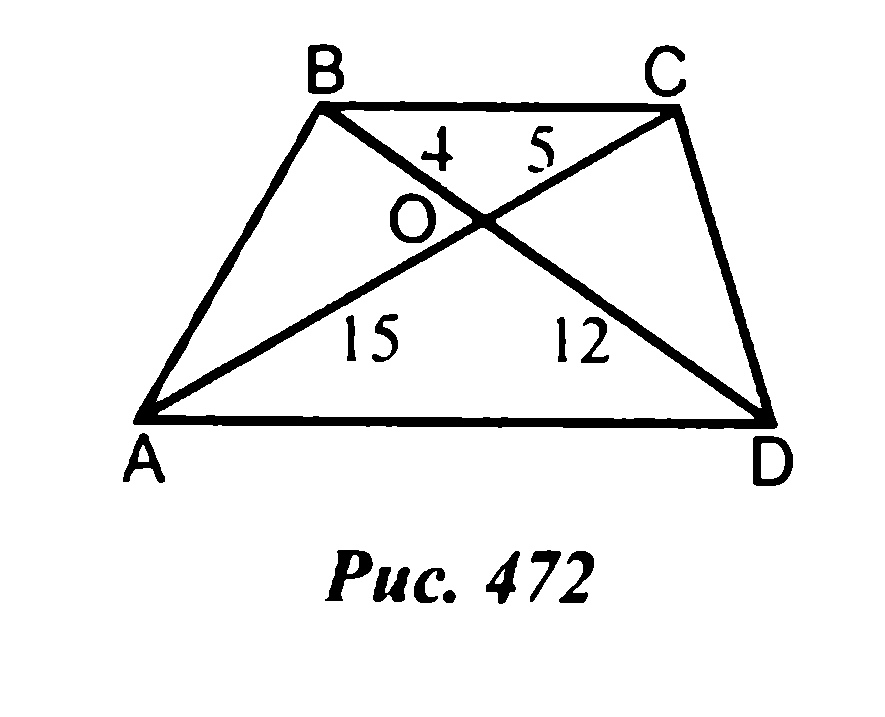
Задания к чертежам Ответы:

После истечения времени проводится взаимопроверка. (5 слайд)

- Поменяйтесь тетрадями с соседом, проверяем правильность решения задач по соответствующему ключу. Ставим напротив задач «плюс» - за правильный ответ, «минус» - за неверное решение.

- Кто не допустил ни одной ошибки? Кто ошибся в 1й, 2й и т.д. задачах? Что вызвало затруднение?

4. Решение задач

- Приступаем к решению более сложных задач.

Задача 1. Дан четырехугольник, по рисунку необходимо сформулировать задачу. Найти: BAD.

- Сформулируйте задачу. (6 слайд)

- Назовите, что дано. Что требуется найти.

- Начертите рисунок в тетрадь и запишите, что дано, что требуется найти.

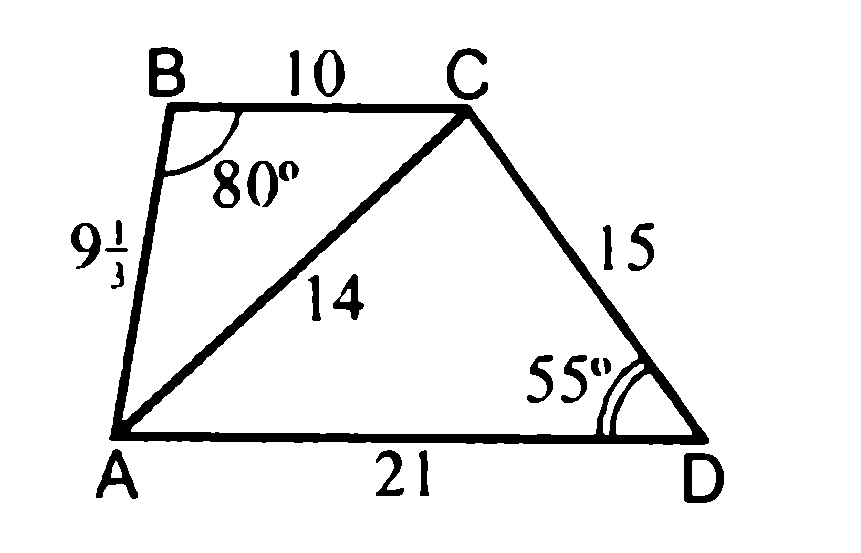Дано: ABCD – четырехугольник,

АС – диагональ,

ВС = 10, СD = 15, AD = 21, AC = 14, АВ = ,

В = 80º, D = 55º.

Найти: BAD.

- Прочитайте, что у вас получилось.

Поиск решения задачи:

- Что нам надо найти? BAD

- Что достаточно знать, чтобы

найти этот угол? ВАС САD

- Откуда мы найдем эти углы? ∆ АВС ∆ ACD

- Если в треугольнике мы знаем один угол, что поможет нам найти другие углы? Для чего даны стороны? (устанавливаем отношение между сторонами, покажем, что треугольники подобны)

- Чему равен коэффициент подобия?

- Что из этого следует? ∆ АВС подобен ∆ ACD

- По какому признаку? (по 3 признаку)

- Что следует из подобия? равенство углов

- Какие углы сможем найти? ВАС САD

- А зная их, найдем… BAD

- План решения понятен? Повторите.

План решения задачи:

- устанавливаем подобие треугольников ∆ АВС и ∆ ACD;

- доказательство подобия, через соотношение сторон;

- устанавливаем равенство соответствующих углов в подобных треугольниках;

- по свойству суммы углов треугольника находим углы ВАС и САD;

- находим угол BAD.

- Женя выходи к доске, оформляй решение этой задачи. Остальные у себя в тетрадях.

Решение:

1. = ;

2. = ∆ АВС подобен ∆ ACD (по 3 признаку);

3. ∆ АВС подобен ∆ ACD = BAC= CAD; BCA= CDA; ABC= ACD (по определению подобных треугольников); BCA= CDA=55º; ABC= ACD=80º;

4. из ∆ АВС: ABC=80º, BCA =55º = BAC=45º; аналогично, из ∆ ACD: ACD=80º, CDA=55º = CAD=45º (по свойству суммы углов треугольника);

5. BAD= ВАС+ САD=45º+45º=90º.

Ответ: BAD=90º.

Задача 2. В параллелограмме ABCD AE – биссектриса угла А. Стороны параллелограмма АВ и ВС относятся как . АЕ пересекает диагональ BD в точке К. Найти отношение . (7 слайд)

- Прочитайте задачу. Что дано в задаче?

- Что нужно найти?

- Давайте сделаем чертеж к задаче (один человек у доски работает Миша).

- Что такое биссектриса угла?

- Обозначим равные углы. Напишем дано, что надо найти.

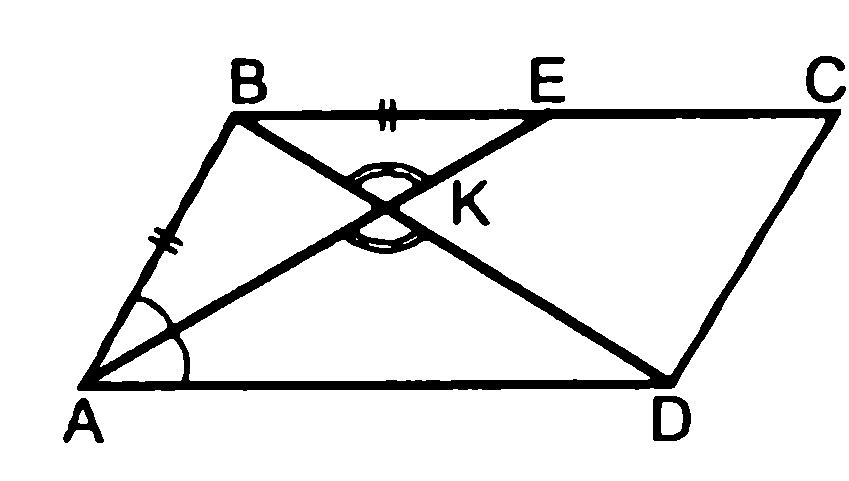Дано: ABCD – параллелограмм,

AE – биссектриса,

.

Найти: .

Поиск решения задачи:

- Что нам надо найти?

- Откуда найдем отношение сторон? ∆ ВКЕ и ∆DКА

- Что будем делать с треугольниками? доказывать подобие

- Что для этого достаточно доказать? BКЕ= DКА – как

вертикальные

ВЕА= ЕАD ( EBD= BDA)

(как накрест лежащие при прямых ВС и АD и секущей АЕ(ВD))

- По какому признаку установили подобие? (по 1 признаку)

- Что следует из подобия? (пропорциональность сходственных

сторон )

- Как связать сторону АВ с нашими подобными треугольниками?

рассмотреть ∆АВЕ

- Каким является этот треугольник? равнобедренным

(углы при основании равны, АВ=ВЕ)

- Что следует из этого равенства? , (т.к. ВС=АD)

- Что можно найти из равенства ? (коэффициент подобия k= )

- Как найти ?

- План решения понятен? Повторите.

План решения задачи:

- устанавливаем подобие треугольников ∆ ВКЕ и ∆ DКА;

- доказательство подобия, через равные углы при параллельных прямых и секущей;

- устанавливаем соотношение сходственных сторон в подобных треугольниках;

- рассматриваем равнобедренный ∆АВЕ, устанавливаем равенство сторон;

- находим коэффициент подобия;

- выявляем отношение .

- Миша оформляет решение у доски, на обороте, остальные самостоятельно, потом сверяем.

Решение:

1. BКЕ= DКА – как вертикальные; ВЕА= ЕАD ( EBD= BDA) (как накрест лежащие при прямых ВС и АD и секущей АЕ(ВD))= ∆ ВКЕ и ∆ DКА подобные (по 1 признаку);

2. ∆ ВКЕ и ∆ DКА подобные = ;

3. расм-м ∆АВЕ: ВЕА= ЕАD, ВАЕ= DАЕ (т.к. АЕ – биссектриса) = ∆АВЕ – равнобедренный;

4. ∆АВЕ – равнобедренный, АВ=ВЕ = устанавливаем ;

5. ВС=АD (противоположные стороны в параллелограмме) = ;

6. = коэффициент подобия k= ;

7. , т.е. .

Ответ: .

- Попробуйте сформулировать свойство биссектрисы угла параллелограмма. Что она сделала с параллелограммом?

Свойство биссектрисы параллелограмма: Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

- Запишите себе это свойство, вы им можете пользоваться и при решении других задач.

Задача 3. Дан треугольник АВС. Прямая MN параллельна стороне АВ, . Отрезок MN равен 20см. Найдите длину отрезка АС. (8 слайд)

- Прочитайте задачу. Сформулируйте, что дано, что нужно найти.

Дано: ∆АВС, MN || AC, ,

MN= 20 см.

Найти: АС.

Поиск решения задачи:

- Что нам надо найти? АС

- Что для этого достаточно рассмотреть? ∆ АВС ∆MBN

- Какими являются эти треугольники? (подобные)

- Что для этого достаточно доказать? BMN= ВАС ( BNM= BCA)

(как накрест лежащие при прямых MN и АС и секущей АВ(СВ))

- По какому признаку установили подобие? (по 1 признаку)

- Что следует из подобия? (пропорциональность сходственных

сторон )

- Что мы найдем из соотношения ? (коэффициент пропорц-ти)

- По какой теореме? (отношение площадей двух подобных треугольнико, равно квадрату коэффициента подобия)

- Коэффициент подобия равен… k=

- Что мы можем найти, зная коэффициент подобия?

MN – известно.

- План решения понятен? Повторите.

План решения задачи:

- устанавливаем подобие треугольников ∆ АВС и ∆MBN;

- доказательство подобия, через равные углы при параллельных прямых и секущей;

- устанавливаем соотношение сходственных сторон в подобных треугольниках;

- зная отношение площадей подобных треугольников, находим коэффициент подобия;

- находим длину стороны АВ, зная коэффициент подобия и длину стороны MN .

- Ход решения понятен? Эту задачку мы записывать в тетрадь не будем.

4 Задача (дополнительно)

Краткое решение

5. Подведение итогов урока (рефлексия)

- Что нового для себя открыли на уроке?

- Какие трудности испытывали при решении задач?

- На что еще стоит обратить внимание на следующем уроке, для закрепления ваших знаний по данной теме?

- Определите свое место на дереве в конце урока. Поднимите руку, кто поднялся выше, кто отпустился, кто остался на месте?

- Самыми активными на уроке были…

6. Домашнее задание

Задание по карточкам.

- Получите домашнее задание. Всем большое спасибо за работу на уроке!