Общая тема: Применение производной ( 15 час.)
Урок № 32 по алгебре и н.м.а. в 11 классе
Тема: Решение задач на составление уравнения касательной
Тип урока: урок закрепления материала
Цели:
Образовательные: формирование навыков и умений составления уравнения касательной, решение задач с применением уравнения касательной к графику функции;
Развивающие: развивать внимание, умения применять теоретические знания на практике;
Воспитательные: воспитание познавательного интереса, самостоятельности.
Формы работы: фронтальная, парная, индивидуальная
Образовательные ресурсы: учебник, презентация, индивидуальные карточки
Ход урока
Организационный момент. Проверка домашнего задания.
Сообщение темы и цели урока
Актуализация опорных знаний
Фронтальный опрос.
1. «Как называется прямая, проходящая через две точки графика функции?»
Ответ учащихся: секущая.
2. «Какая прямая называется касательной к кривой L в точке M?».
Слайд № 4

Учащиеся должны ответить, что касательная есть предельное положение секущей.
3. «Как найти угловой коэффициент касательной?»
 Слайд № 5.
Слайд № 5.
Ответ: угловой коэффициент касательной 
4. «В чем состоит геометрический смысл производной?»
 Слайд № 6
Слайд № 6
Ответ: Если к графику функции  в точке с абсциссой x = a можно провести касательную, непараллельную оси y, то f ′(a) выражает угловой коэффициент касательной, а так как
в точке с абсциссой x = a можно провести касательную, непараллельную оси y, то f ′(a) выражает угловой коэффициент касательной, а так как  , то f ′(a)=
, то f ′(a)=  .
.
5. «Что можно сказать о знаке производной функции в точке x0, если касательная, проведенная к графику функции в точке с абсциссой x0, образует с положительным направлением оси абсцисс острый угол?»
Слайд № 7

Ответ: Производная в точке x0 положительна.
6. «Что можно сказать о знаке производной функции в точке x0, если касательная, проведенная к графику функции в точке с абсциссой x0, образует с положительным направлением оси абсцисс тупой угол?»
Слайд № 8

Учащиеся отвечают, что в этом случае производная в точке x0 отрицательна.
7. «Что можно сказать о значении производной в том случае, когда касательная к графику функции в точке с абсциссой x0 параллельна оси абсцисс?»
Слайд № 9

Ответ: Производная этой функции в точке x0 равна нулю.
8. Записать на доске уравнение касательной к графику функции y = f (x) в точке с абсциссой x0: y = f (x0) + f ′(x0)(x – x0)
Слайд № 11
На рисунке изображен график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
Ответы:
Слайды № 12 – 14

На рисунке изображен график производной функции у = f '(х). Найдите угловой коэффициент касательной к графику функции y = f(x) в точке с абсциссой х0 = 2. |
Найдите значение производной  .
.
Функция у = f(x) определена на промежутке (−4; 4). На рисунке изображён график её производной. Определите по графику у = f '(x) градусную меру угла наклона касательной к положительному направлению оси Ох в точке с абсциссой x0 = − 2 .
|
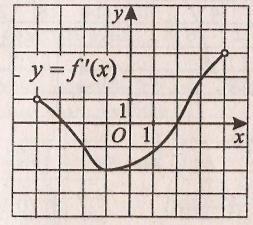
Ответы:
Решение задач
№ 5.25 (а,в), 5.31(а,в) – фронтальная работа у доски
5. самостоятельная работа
Учитель выдает задания для самостоятельной работы.
Для учащихся 1-й группы учителем составлены карточки уровня А в двух вариантах.
Уровень А
Вариант 1
Найдите угловой коэффициент касательной, проведенной к графику функции  в его точке с абсциссой
в его точке с абсциссой  .
.
| 1) | 22 | 2) | 23,75 | 3) | 24,25 | 4) | 24 |
На графике функции  взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси ОХ под углом, тангенс которого равен 5. Найдите абсциссу точки А.
взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси ОХ под углом, тангенс которого равен 5. Найдите абсциссу точки А.
| 1) | 1 | 2) | 3 | 3) | 
| 4) | 2 |
| 3. На рисунке изображен график функции  и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой  . Найдите значение производной в точке . Найдите значение производной в точке  . .
|
Вариант 2
Найдите угловой коэффициент касательной, проведенной к графику функции  в его точке с абсциссой
в его точке с абсциссой  .
.
Определите абсциссу точки, в которой касательная к графику функции  параллельна оси абсцисс.
параллельна оси абсцисс.
| 3. На рисунке изображен график функции  и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой  . Найдите значение производной в точке . Найдите значение производной в точке  . .
|
Ответы:
| Номер задания | 1 | 2 | 3 |
| Вариант 1 | 3 | 4 | 1,5 |
| Вариант 2 | 1 | 2 | −1 |
Итоги урока.
.
1. На уроке мы изучили и на примере разобрали ответы на вопросы:
Что называется касательной к графику функции в точке?
В чем заключается геометрический смысл производной?
Сформулируйте алгоритм нахождения уравнения касательной?
Домашнее задание: решить № 5.24(а,в),/ 5.31 (б,г)








 Слайд № 5.
Слайд № 5.
 Слайд № 6
Слайд № 6 в точке с абсциссой x = a можно провести касательную, непараллельную оси y, то f ′(a) выражает угловой коэффициент касательной, а так как
в точке с абсциссой x = a можно провести касательную, непараллельную оси y, то f ′(a) выражает угловой коэффициент касательной, а так как  , то f ′(a)=
, то f ′(a)=  .
.


 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке 




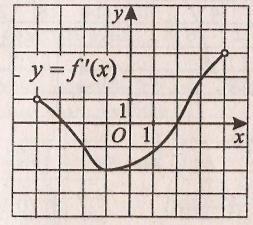
 в его точке с абсциссой
в его точке с абсциссой  .
. взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси ОХ под углом, тангенс которого равен 5. Найдите абсциссу точки А.
взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси ОХ под углом, тангенс которого равен 5. Найдите абсциссу точки А. 










