Обучение школьников решению задач данного типа
с позиции деятельностного подхода
Тема: Составление уравнения касательной к графику данной функции,
параллельной данной прямой
Цели:
Обучающая: ПРАКТИЧЕСКИЕ УМЕНИЯ
закрепление понятия касательной к графику функции в точке и понимания геометрического смысла производной;
совершенствование умения составления уравнения касательной к графику заданной функции в данной точке;
вывод алгоритма составления уравнения касательной, параллельной данной прямой;
формирование умения применения алгоритма для конкретных функций.
Развивающая: ТЕОРЕТИЧЕСКИХ УМЕНИЙ
самоконтроля посредством соотнесения этапов решения эталонам;
развитие математического интереса, логического мышления, исследовательских навыков посредством организации поиска решения заявленной задачи;
математической речи посредством организации этапа громкой речи;
умений планирования при организации применения алгоритма решения;
контроля посредством написания контролирующей работы и проверки правильности решения по предъявленным ответам.
Воспитывающая: ЛИЧНОСТНЫЕ КАЧЕСТВА
формирование у школьников усидчивости, самостоятельности, навыков самоорганизации и самоконтроля.
Оборудование урока:
Интерактивная доска или проектор, раздаточный материал (карточки-опоры)
справочные таблицы на стенах следующего содержания:
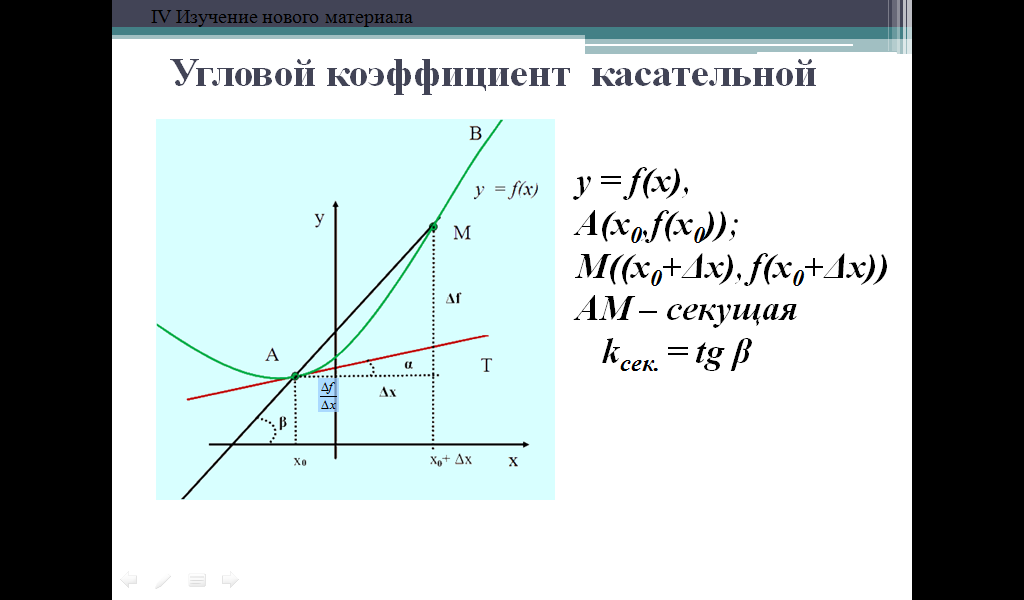


Ход урока
Организационный момент, сообщение обучающей цели урока (цель заявлена темой урока)
Актуализация опорных знаний (мотивационно-ориентировочный этап)
Цель этапа: актуализация знаний, необходимых для усвоения темы:
понятия касательной к графику функции;
признака параллельности прямых;
знание формулы касательной в различных интерпретациях;
алгоритма решения задачи по известной абсциссе точки касания.
Ответьте на вопросы:
Вопросы могут быть предложены учащимся фронтально по одному, или предъявляться всем списком с последующим обсуждением ответов (с самопроверкой).
Согласны ли вы с утверждением: «Касательная – это прямая, имеющая с данной кривой одну общую точку»? Почему? Объясните, используя чертежи:
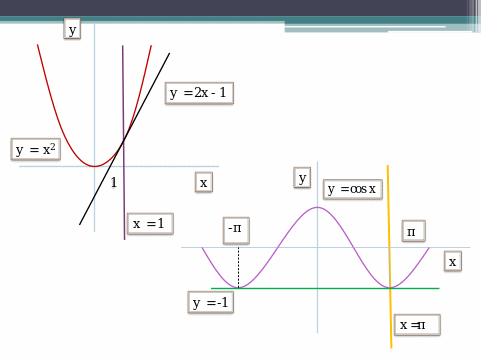
Какие из указанных прямых параллельны? у = 0,5х; у = - 0,5х;
у = 0,5 - 0,5х. Почему?
Выберите, по крайней мере, один вариант верного уравнения касательной из предложенных:
y = f''(x0) + f(x0)(x - x0)
y = f''(x0)(x - x0) + f(x0) ٧
y= f''(x0)x + f(x0) - x0
y= f''(x0)x + f(x0) - f''(x0)x0 ٧
Какую ключевую задачу с касательной к графику заданной функции вы знаете? Повторим алгоритм ключевой задачи 1.
Задачи на повторение могут быть заданы по усмотрению учителя: либо заранее двум учащимся с последующей проверкой или сверкой с готовым решением, заготовленным учителем на экран; или быть заданными для самостоятельного решения всему классу с последующей самопроверкой с решением на экране.
Ключевая задача 1. Составление уравнения касательной, если задана точка касания
Составьте уравнение касательной к графику функции у=х2–2х–3 в точке с абсциссой х0=2.
Решение:
1. Обозначим абсциссу точки касания а, тогда, а=2.
2. Найдем ординату точки касания f(a): f(2)= - 3
3. Найдем производную данной функции и значение производной в точке касания f’ (x) и f’(a): f’(x)=2x–2, f’(a)=2.
4. Подставим найденные числа f(a), f‘(a) в общее уравнение касательной
у = f(a) + f’(a)(x–a): у=-3+2(х–2), у=-3+2х–4,
у = 2х–7 – уравнение касательной. Ответ: у=2х –7.
2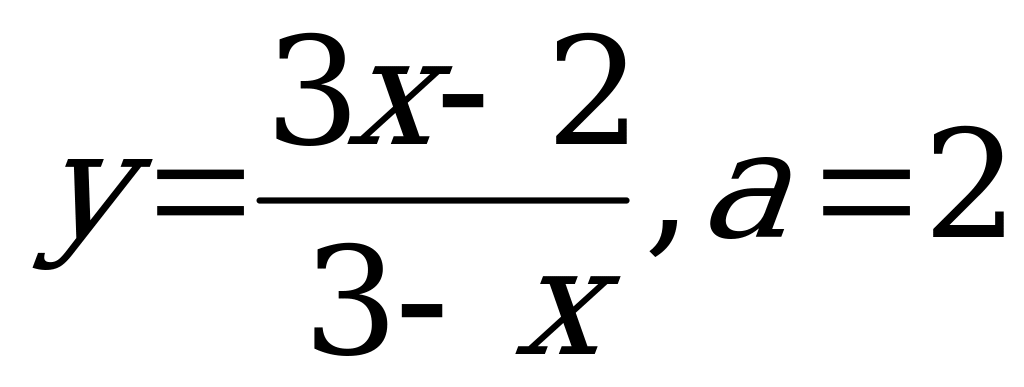 . Составьте уравнение касательной к графику функции у =f (x) в точке с абсциссой х = а, если
. Составьте уравнение касательной к графику функции у =f (x) в точке с абсциссой х = а, если
Решение:
О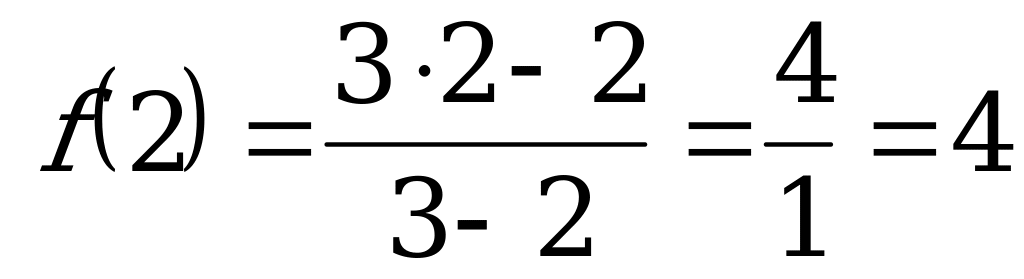 бозначим абсциссу точки касания а, тогда, а=2.
бозначим абсциссу точки касания а, тогда, а=2.
Найдем ординату точки касания f(a):
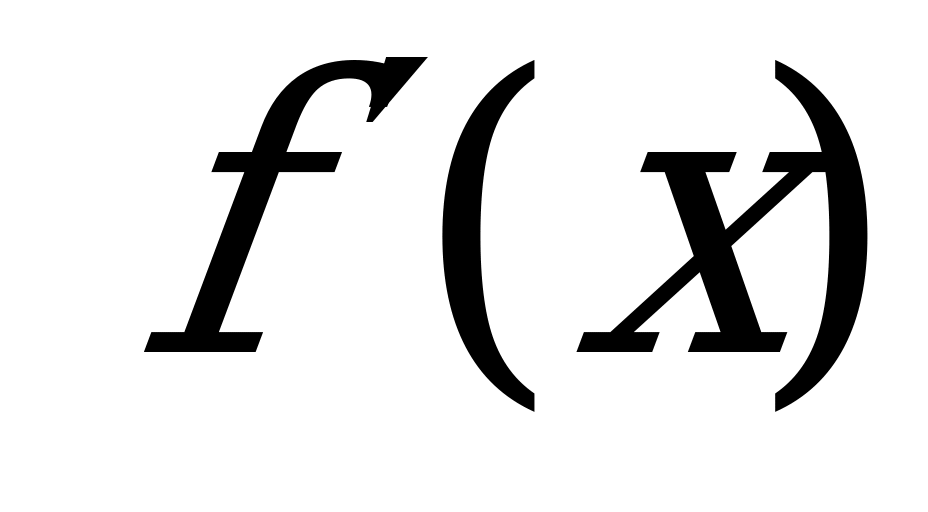
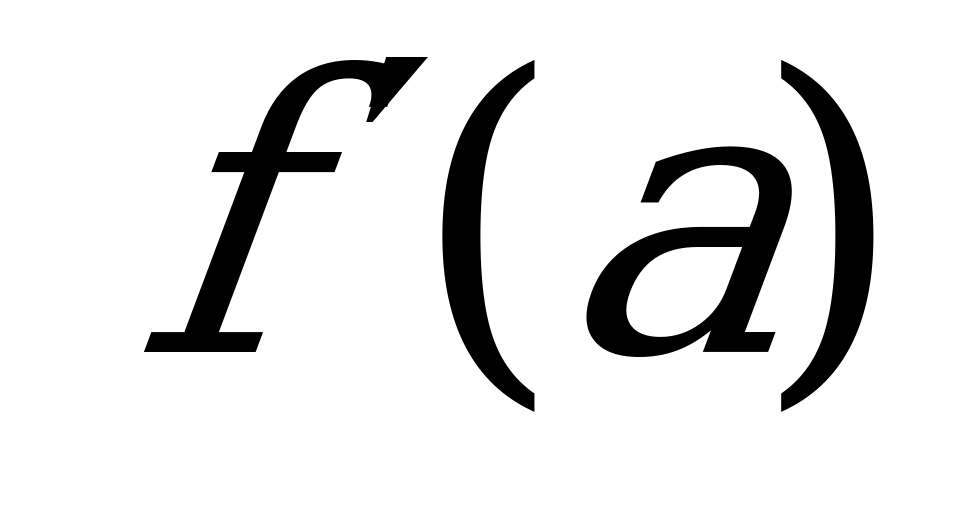
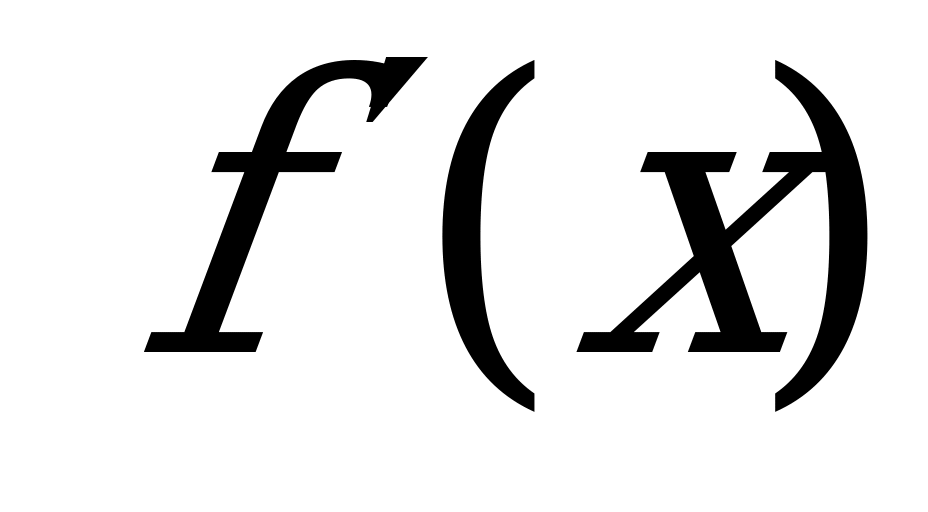
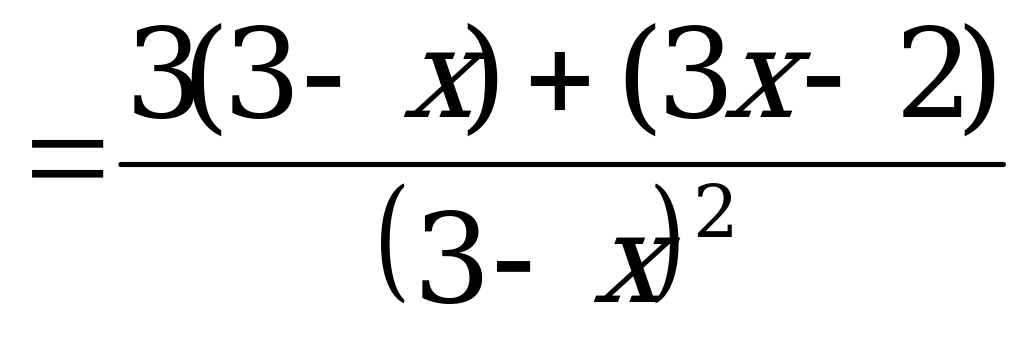
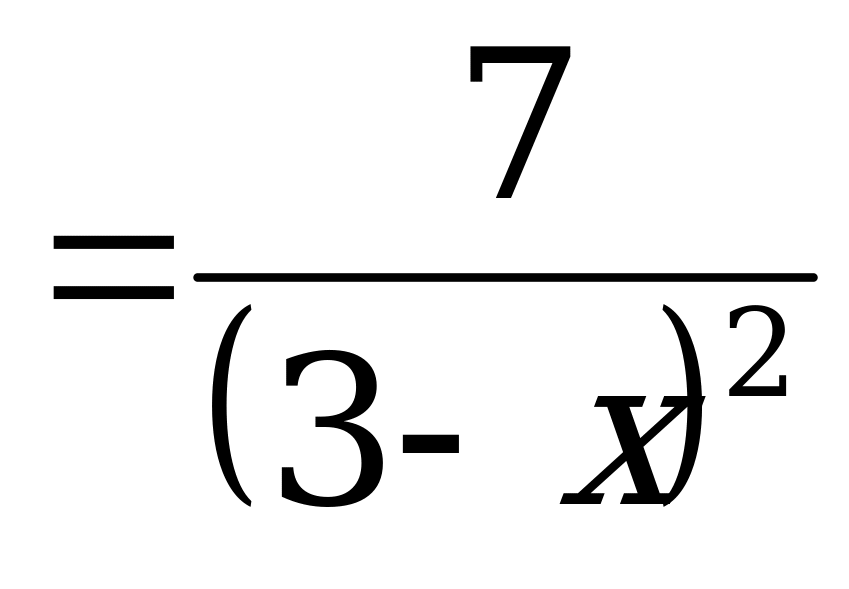
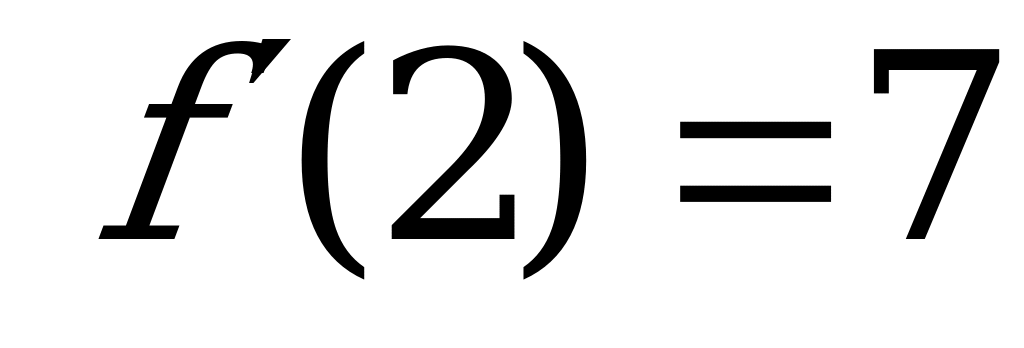 Найдем производную данной функции и значение производной в точке касания и :
Найдем производную данной функции и значение производной в точке касания и :
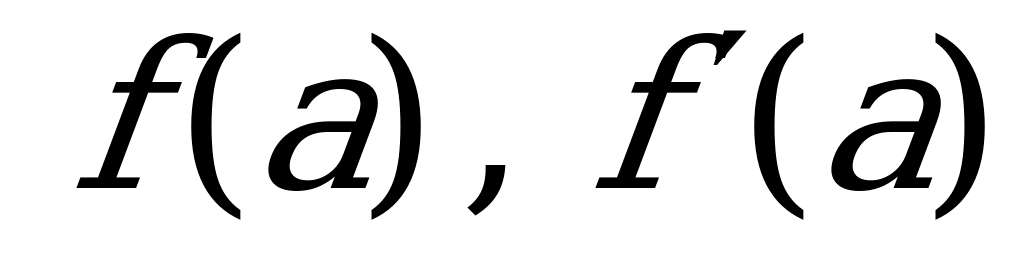
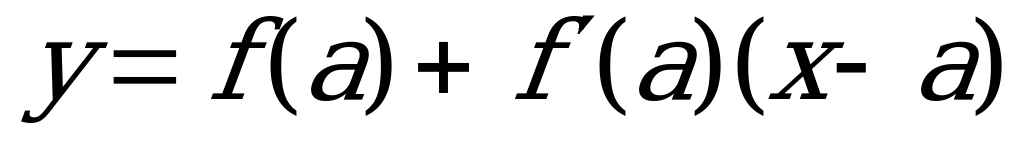 4. Подставим найденные значения в общее уравнение касательной
4. Подставим найденные значения в общее уравнение касательной
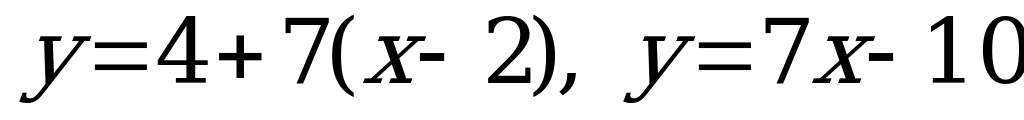
Ответ: у=7х –10 – искомое уравнение касательной.
1-й этап – мотивационный. Происходит предварительное ознакомление учащихся с целью обучения, создание «внутренней», или познавательной, мотивации. Для создания познавательной мотивации можно использовать проблемные ситуации.
Цель этапа: подведение учащихся к мысли о вариативности данных в изученной задаче составления уравнения касательной и вычленение возможных вариантов данных.
Выберите данные, необходимые для составления уравнения касательной к графику заданной функции в данной точке:
точка касания;
абсцисса точки касания;
ордината точки касания;
формула функции, к графику которой будет проведена касательная;
формула производной данной функции для нахождения значения производной в точке касания;
значения производной в точке (точках) касания;
угол наклона касательной к положительному направлению оси абсцисс;
тангенс угла наклона между касательной и положительным направлением оси абсцисс;
коэффициент k в уравнении касательной y = kx + b.
В результате нужно подвести к следующим рассуждениям:
из первых двух вариантов в задаче могут быть заданы каждый, но достаточно второго;
варианты с) и f) могут быть получены с помощью расчетов;
вариант ответа e) может быть получен самостоятельно, с помощью правил дифференцирования функций и таблицы производных;
последние 4 варианта из предложенных ответов могут быть взаимнозаменимы, либо получены один из другого.
Вывод: данные в задаче можно варьировать. Для составления уравнения касательной необходимо иметь как минимум 2 данных: формулу функции и абсциссу точки касания (это заложено в формуле касательной).
Объявление цели сегодняшнего занятия: Целью сегодняшнего занятия является изучение одной из таких вариационных задач, когда вместо одного из необходимых данных, а именно – абсциссы точки касания – предъявляется некая прямая, заданная формулой линейной функции y = kx + b , параллельная искомой касательной.
Вопрос: как вы будете решать задачу?
На следующем этапе надо организовать обсуждение предлагаемых вариантов решения.
Изучение нового материала
Цель этапа: составление алгоритма решения задачи написания уравнения касательной, параллельной графику данной прямой, формирование ориентировочной основы действия.
Учащимся объявляется, что цель сегодняшнего занятия – разобрать алгоритм только одного из видов заданий, а именно: Ключевая задача 2. Составление уравнения касательной к графику данной функции, параллельной данной прямой.
Итак, теперь у нас 2 ключевые задачи:
Составление уравнения касательной 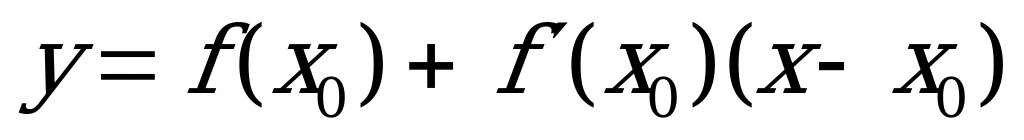 в точке;
в точке;
Нахождение точки (точек) касания: по условию параллельности прямых;
Учащимся предлагается объяснить готовые решения задач, косвенно связанных с новой темой. На экране предъявляются две задачи с решениями, которые обсуждаются, акцент делается на момент приравнивания значения производной в точке угловому коэффициенту из уравнения прямой, параллельной касательной.
Нахождение точки (точек) касания
В какой точке касательная к графику функции у = х² параллельна прямой
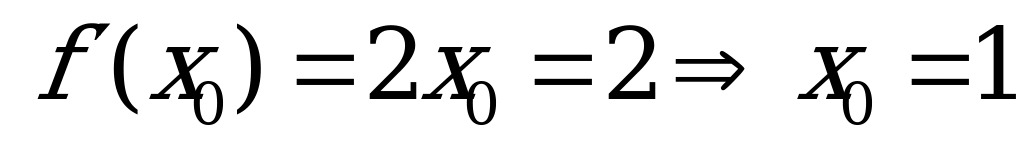
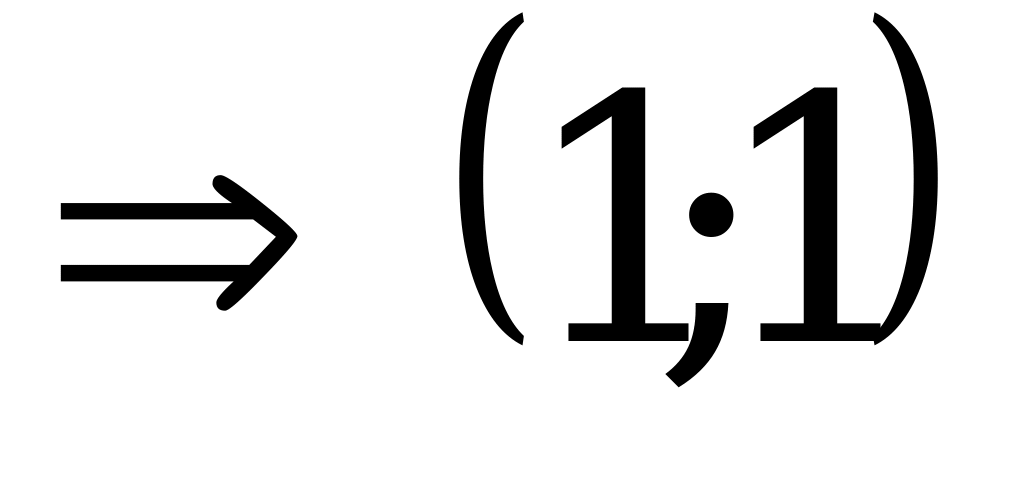 у = 2х+1?
у = 2х+1?
Решение:
Ответ: (1; 1) - координаты точки касания
2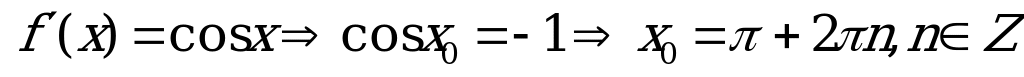 . В какой точке касательная к графику функции у =sinx параллельна прямой у = - х?
. В какой точке касательная к графику функции у =sinx параллельна прямой у = - х?
Р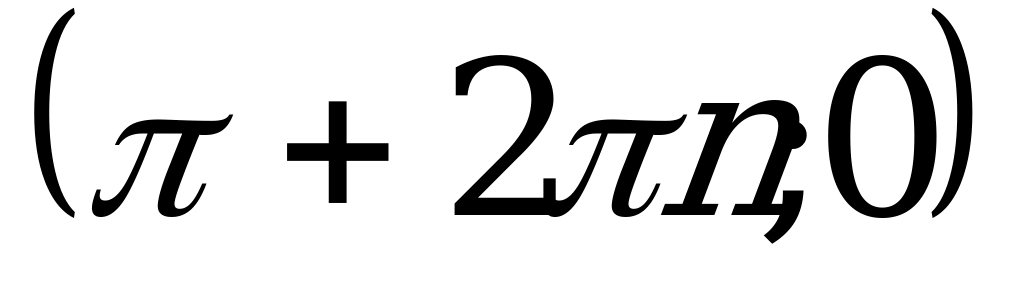 ешение:
ешение:
Ответ: - координаты точек касания.
2-й этап – составление схемы ориентировочной основы действия (ООД). Ученик разбирается в содержании усваиваемого действия: в свойствах предмета, в результате-образце, в составе и порядке исполнительных операций.
Цель этапа: поиск и составление алгоритма решения новой для них задачи. Учащимся предъявляется задача с решением, но решение открывается строка за строкой после того, как ученики «найдут» следующий шаг решения. Учитель может стимулировать активность ребят наводящими вопросами.
Напишите уравнения всех касательных к графику функции у = х2–2х–8, параллельных прямой у = - 4х – 4. |
Обозначим абсциссу точки касания а; | Пусть x0=а – абсцисса точки касания |
Найдем (выразим) ординату точки касания f(a); | f(a) = a2 – 2a –8 |
Найдем (выразим) производную функции f’(x) и значение производной в точке касания f’(a); | f’(x) = 2x – 2, f’(a) = 2a – 2 |
Из уравнения данной прямой определяем значение углового коэффициента k. Из геометрического смысла производной и условия параллельности прямых следует f’(a)= k; | f’(a)= k = - 4; |
Решим уравнение f’(a)= k, получим значение а; | 2a – 2 = - 4; a = - 1 – абсцисса точки касания; |
Вычислим ординату точки касания f(a) | f(a) = f (-1) = - 5;
|
Подставим найденные числа а, f(a),f‘(a)=k в общее уравнение касательной у = f(a) + f’(a) (x - a): | y = -5 – 4(x+1), y = - 4x – 9 – уравнение касательной. |
| Ответ: y= - 4x–9. |
Первичное закрепление нового материала (этап уяснения знаний)
 Учащимся предлагается алгоритм-памятка решения задачи в виде фрагмента тетради с печатной основой:
Учащимся предлагается алгоритм-памятка решения задачи в виде фрагмента тетради с печатной основой:
Решение:
1. Пусть а- ______________________________________________;
2. Найдем (выразим) ___________________________________________ f (a) = ……;
3. Найдем (выразим) __________________ и__________________________ f’(a)=….;
4. Но, с другой стороны, f’(a)=k, где k – угловой коэффициент в уравнении данной прямой (условие параллельности).
Решим уравнение … =… , получим a = …. - _______________________точек касания;
5. Вычисляем _________________________________ f (a) = …. (или несколько f (a) =…);
6. Подставим найденные числа а, f(a),f‘(a) в _____________________________касательной
у = f(a) + f’(a)(x - a):
y =… х +… (или несколько у = ... х + … ) - уравнения касательных.
 Сначала учащимся предлагается заполнить пропуски в данном руководстве (это можно сделать с самопроверкой с доски).
Сначала учащимся предлагается заполнить пропуски в данном руководстве (это можно сделать с самопроверкой с доски).
Ответы:
абсцисса точки касания
ординату точки касания
производную и значение производной в точке касания
абсцисса (сы)
ординату точки касания
общее уравнение
ВОПРОСЫ:
К чему (к каким действиям) сводится решение ДАННОЙ задачи?
Сколько и каких данных требуется для решения ДАННОЙ задачи?
Полученные заполненные опоры остаются у учеников.
Затем учащимся предлагается решить задачу, используя данный алгоритм, используя карточку-инструктаж (материализованная основа действия), в которой предлагается заполнить пропуски.
Лучше вызвать к доске ученика, который может громко вслух комментировать действия.
3-й этап – формирование действия в материальной или материализованной форме. Действие выполняется как внешнее, практическое, с реальными предметами (материальная форма действия), например, перекладывание каких-либо предметов при счете. Действие выполняется с преобразованным материалом: моделями, схемами, диаграммами, чертежами и т. п. (материализованная форма), например счет на палочках. При этом все операции действия осознаются, а замедленное их выполнение позволяет увидеть и осознать содержание как операций, так и всего действия в целом. Обязательным условием этого этапа является сочетание материальной формы действия с речевой, что позволяет отделить усваиваемое действие от тех предметов или их заместителей, с помощью которых оно выполняется. Когда действие начинает протекать плавно, безошибочно и более быстро, убираются ориентировочная карточка и материальные опоры.
Цель данного этапа: пошаговый контроль своих действий.
|
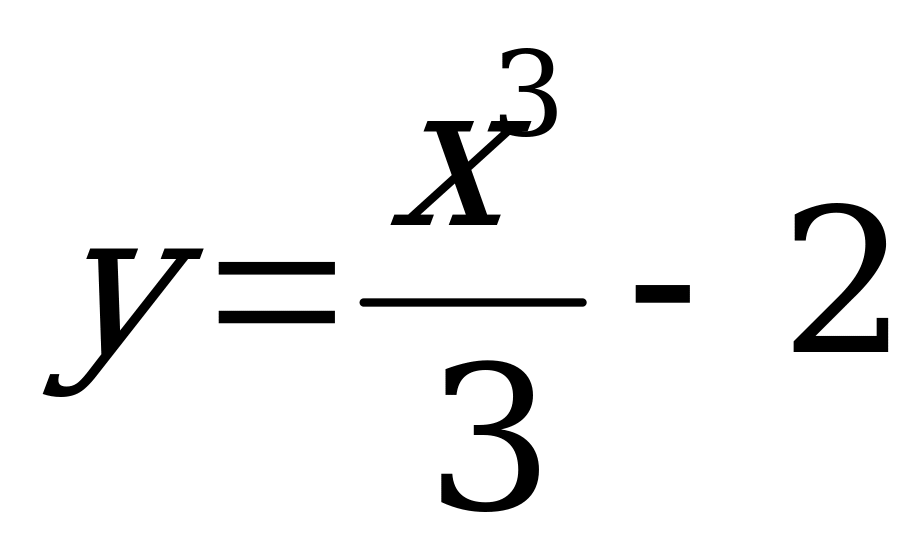 2.Напишите уравнения всех касательных к графику функции , параллельных данной прямой, заданной формулой y = 9x - 5. 2.Напишите уравнения всех касательных к графику функции , параллельных данной прямой, заданной формулой y = 9x - 5.
|
| Обозначим абсциссу точки касания а;
| Пусть а - … точки касания |
| Найдем (выразим) f(a) 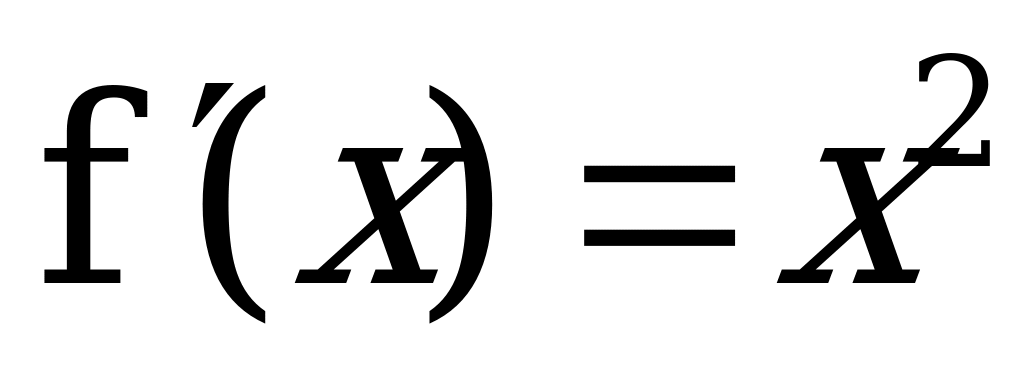
| 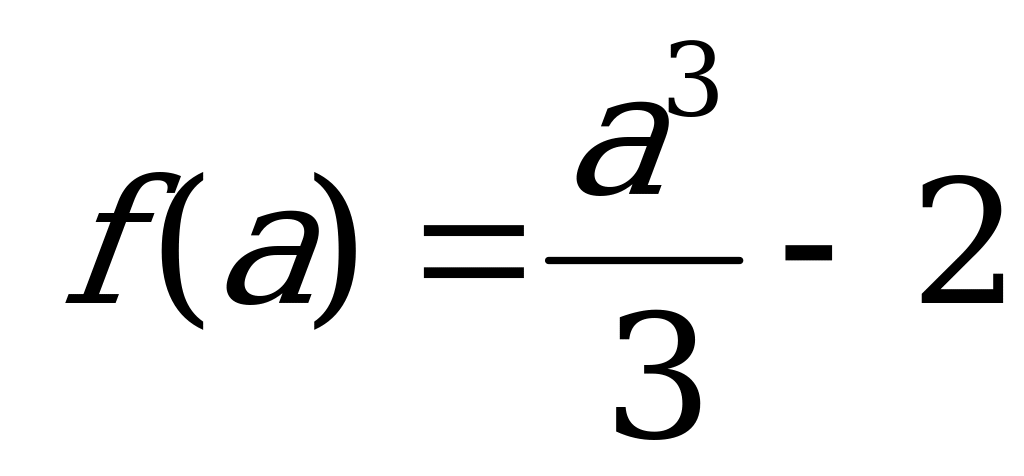
|
| Найдем (выразим) , затем f′(…) | 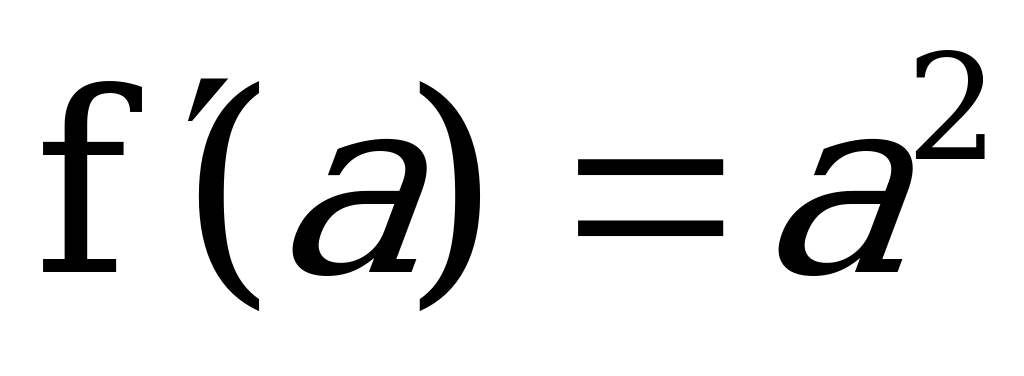
|
| Из уравнения данной прямой определяем значение углового коэффициента k = 9. | f’(a)= … (условие параллельности). |
| Решим уравнение , получим - абсциссы точек касания | 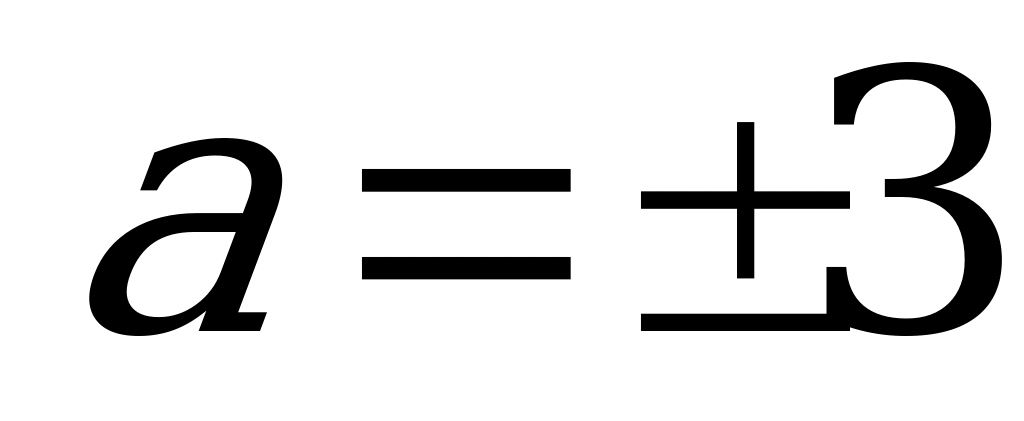
|
| Вычислим f1 (a) =… или f2 (a) = …. | f1 (a) = 7 или f2 (a) = -…. |
| Подставим найденные числа а, f(a),f‘(a) в общее уравнение касательной у = f(a) + f’(a)(x - a) | y = …х - 20 или у = …х + 16 - уравнения касательных. |
| Ответ: у=9х-20 или у=9х+16 |
Работа в парах: учащимся предлагается на местах решить следующую задачу, проговаривая вполголоса алгоритм решения по карточке-опоре:
|
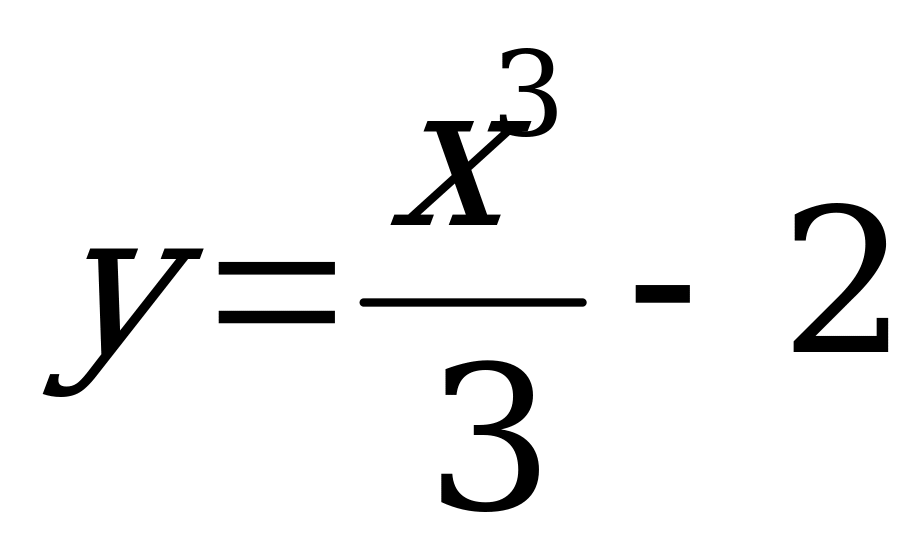 Напишите уравнения всех касательных к графику функции , параллельных данной прямой, заданной формулой y = x – 3. Напишите уравнения всех касательных к графику функции , параллельных данной прямой, заданной формулой y = x – 3.
|
| Обозначим абсциссу точки касания а;
| Пусть а - … точки касания |
| Найдем (выразим) f(a)
| 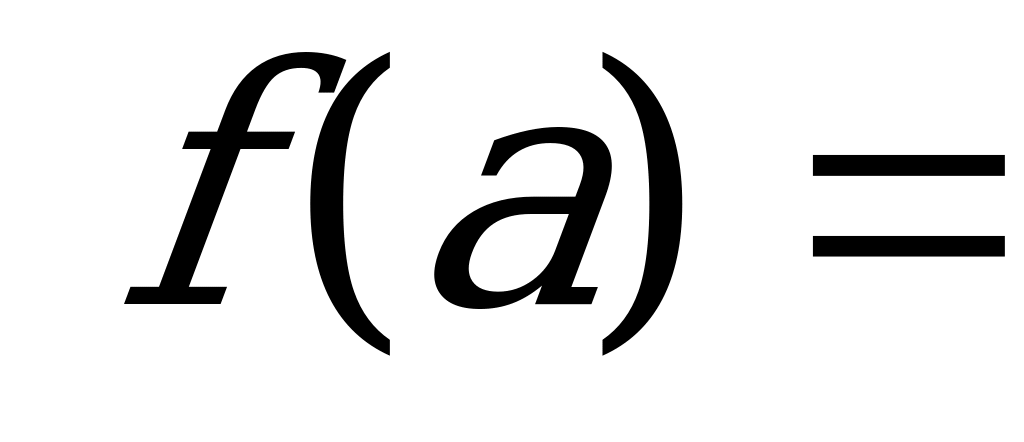 … …
|
| 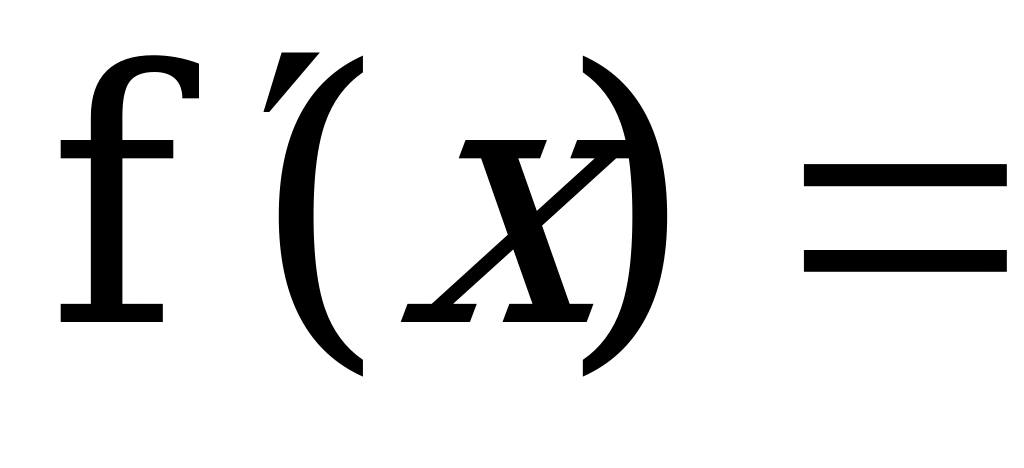 Найдем (выразим) , затем f′(…) Найдем (выразим) , затем f′(…)
| 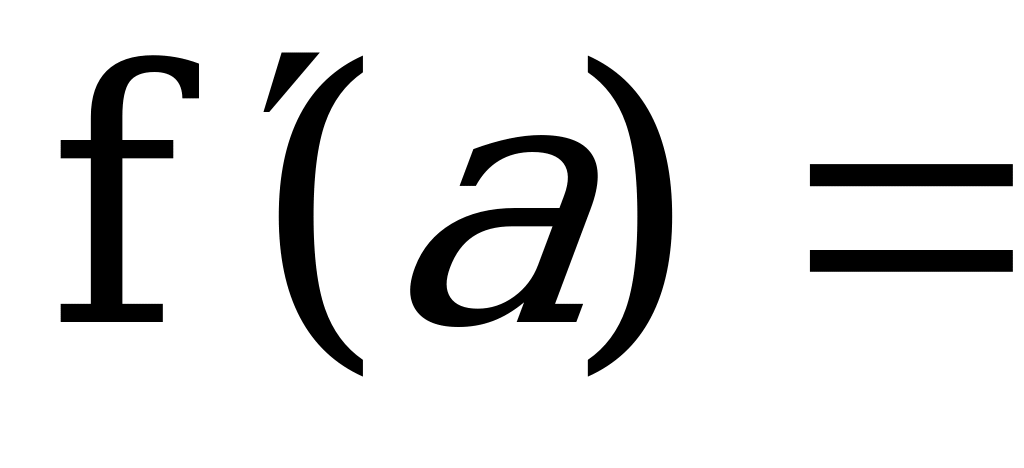 … …
|
| Из уравнения данной прямой определяем значение углового коэффициента k = . | f’(a)= … (условие параллельности). |
| Решим уравнение , получим - абсциссы точек касания | 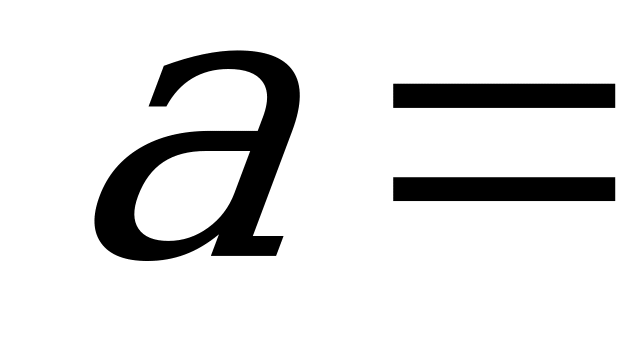 ….. …..
|
| Вычислим f1 (a) =… или f2 (a) = …. | f1 (a) = 7 или f2 (a) = -…. |
| Подставим найденные числа а, f(a),f‘(a) в общее уравнение касательной у = f(a) + f’(a)(x - a) | y = … или у = … - уравнения касательных. |
| Ответ: у=… или у=… |
Учитель предлагает ребятам использовать карточки-опоры и решить задания у доски и на местах, воссоздавая весь алгоритм, с громким проговариванием у доски, с уточнениями и дополнениями класса с мест.
4-й этап – формирование действия в громкой речи. Ученик, лишенный материальных опор действия, анализирует материал в плане в громкой социализированной речи, обращенной к другому человеку. Это одновременно и речевое действие, и сообщение об этом действии. Речевое действие должно быть развернутым, сообщение – понятным другому человеку, контролирующему процесс обучения. На этом этапе происходит «скачок» – переход от внешнего действия к мысли об этом действии. Осваиваемое действие проходит дальнейшее обобщение, но остается несокращенным, неавтоматизированным.
К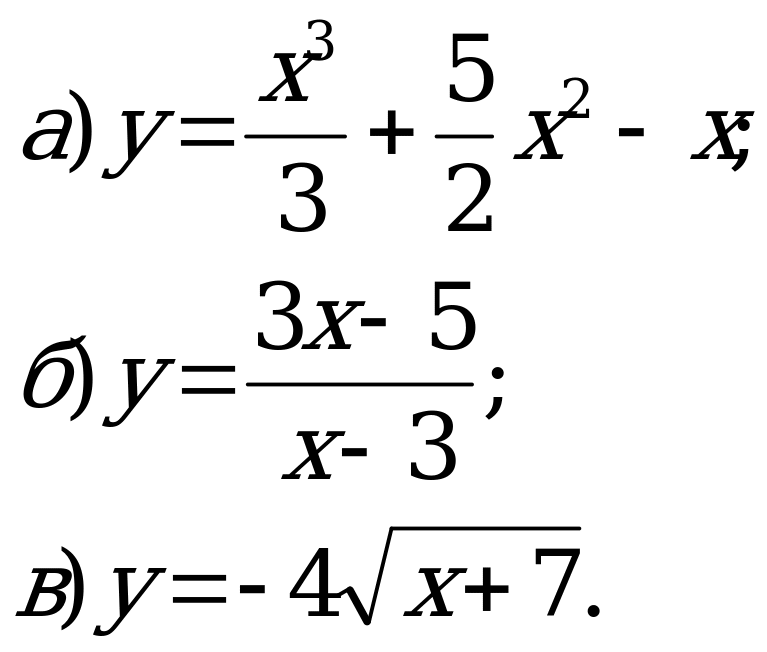 графику заданной функции проведите касательную так, чтобы она была параллельна прямой y = 2 – x:
графику заданной функции проведите касательную так, чтобы она была параллельна прямой y = 2 – x:
Закрепление нового материала (этап отработки того, что уяснено)
Цель этапа: формирование умения решать задачу посредством пошагового контроля и самоконтроля своих действий (тренинг по алгоритму)
5-й этап – формирование действия во внешней речи «про себя». Ученик использует ту же речевую форму действия, что и на предыдущем этапе, но без проговаривания (даже шепотом). Здесь возможен пооперационный контроль: педагог может уточнять последовательность производимых операций или результат отдельной операции. Этап завершается, когда достигается быстрое и правильное выполнение каждой операции и всего действия.
Т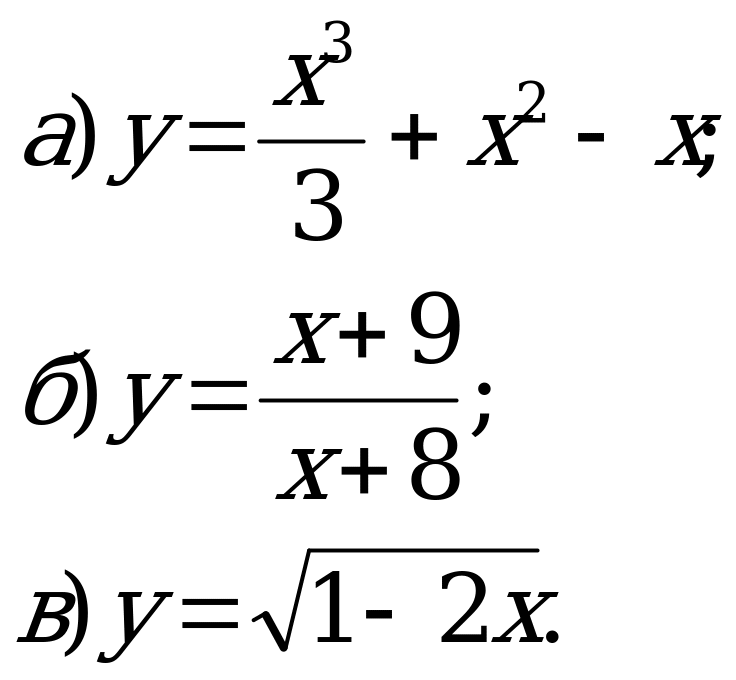 ренировочные упражнения: К графику заданной функции проведите касательную так, чтобы она была параллельна прямой y = 2 – x:
ренировочные упражнения: К графику заданной функции проведите касательную так, чтобы она была параллельна прямой y = 2 – x:
Ответы: а),б),в)
6-й этап – формирование действия во внутренней речи. Ученик, решая задачу, сообщает только конечный ответ. Действие становится сокращенным и легко автоматизируется. Но это автоматизированное действие, выполняемое с максимально возможной для ученика скоростью, остается безошибочным (при появлении ошибок необходимо вернуться на один из предыдущих этапов). На последнем, шестом, этапе формируется умственное действие, появляется «феномен чистой мысли».
Цель этапа: совершенствование умения решать задачу посредством свертывания действия (сворачивание шагов некоторых алгоритма.
П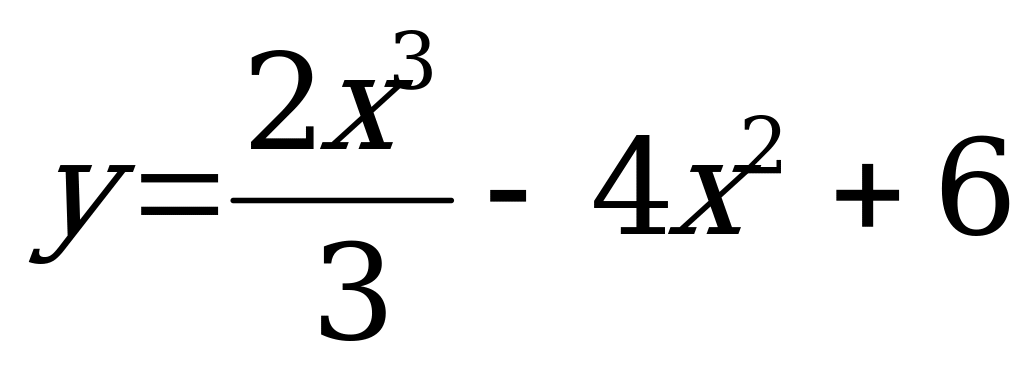 рямая у = 7х - 5 параллельна касательной к графику функции у = х2 + 6х - 8. Найдите абсциссу точки касания.
рямая у = 7х - 5 параллельна касательной к графику функции у = х2 + 6х - 8. Найдите абсциссу точки касания.
Составьте уравнение всех касательных к графику функции , параллельных прямой y = - 6x +5
Ответьте на теоретические вопросы
Как формулируется задача, изученная вами сегодня на уроке?
К чему (к каким действиям) сводится решение данной задачи?
Сколько и каких данных требуется для решения данной задачи?
Контроль знаний
Цель данного этапа: контроль правильности усвоения знаний посредством решения заданий и проверки правильности решения по предъявленным на экране ответам, развитие контроля и самоконтроля.
| 1 вариант | 2 вариант |
Прямая у = 6х + 8 параллельна касательной к графику функции у = х2 - 3х + 5. Найдите абсциссу точки касания. | 1.Прямая у = 7х + 1 параллельна касательной к графику функции у = х2+ 8х + 6. Найдите абсциссу точки касания. |
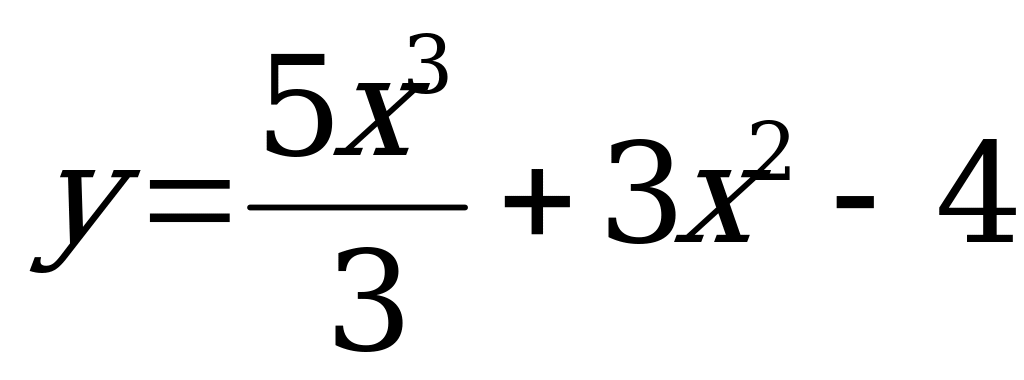 Составьте уравнение всех касательных к графику функции , Составьте уравнение всех касательных к графику функции ,
параллельных прямой y = - x +2 . | 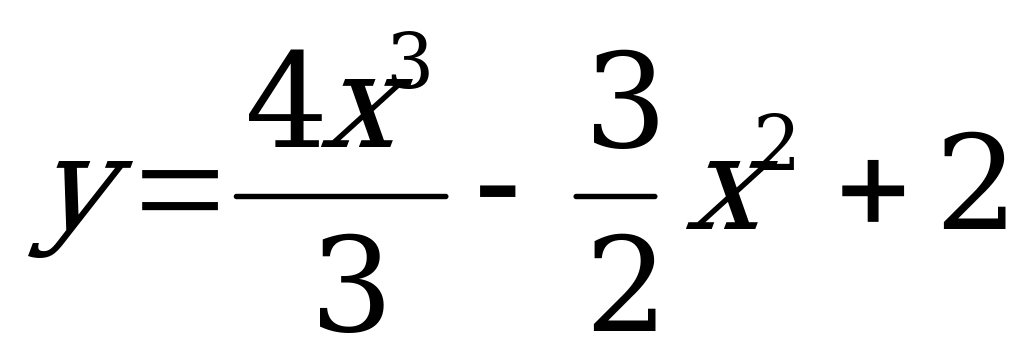 2. Составьте уравнение всех касательных к графику функции , 2. Составьте уравнение всех касательных к графику функции , параллельных прямой y = - x - 5 . |
Напишите по памяти краткий алгоритм решения задачи, изученной сегодня на уроке. | 3.Напишите по памяти краткий алгоритм решения задачи, изученной сегодня на уроке. |
Подведение итогов. Самопроверка по готовым ответам.












 Учащимся предлагается алгоритм-памятка решения задачи в виде фрагмента тетради с печатной основой:
Учащимся предлагается алгоритм-памятка решения задачи в виде фрагмента тетради с печатной основой: Сначала учащимся предлагается заполнить пропуски в данном руководстве (это можно сделать с самопроверкой с доски).
Сначала учащимся предлагается заполнить пропуски в данном руководстве (это можно сделать с самопроверкой с доски).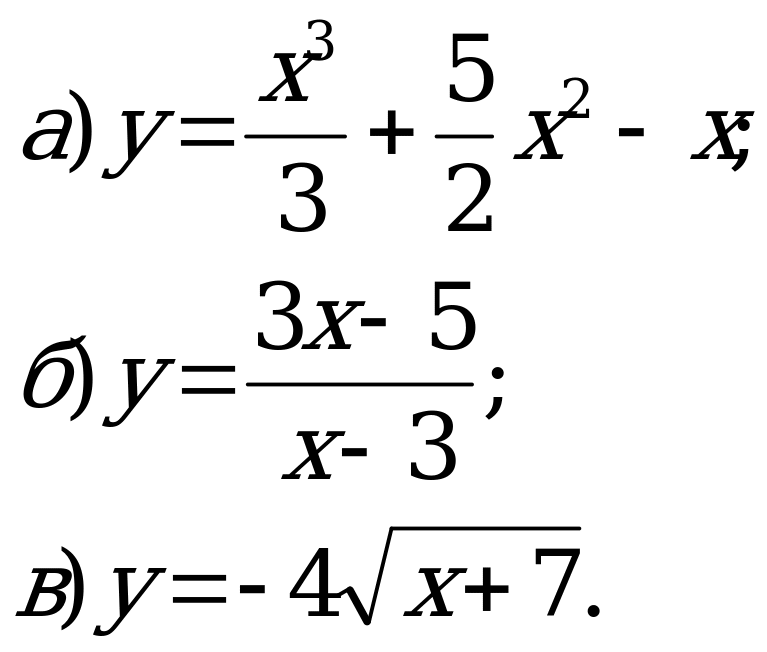 графику заданной функции проведите касательную так, чтобы она была параллельна прямой y = 2 – x:
графику заданной функции проведите касательную так, чтобы она была параллельна прямой y = 2 – x: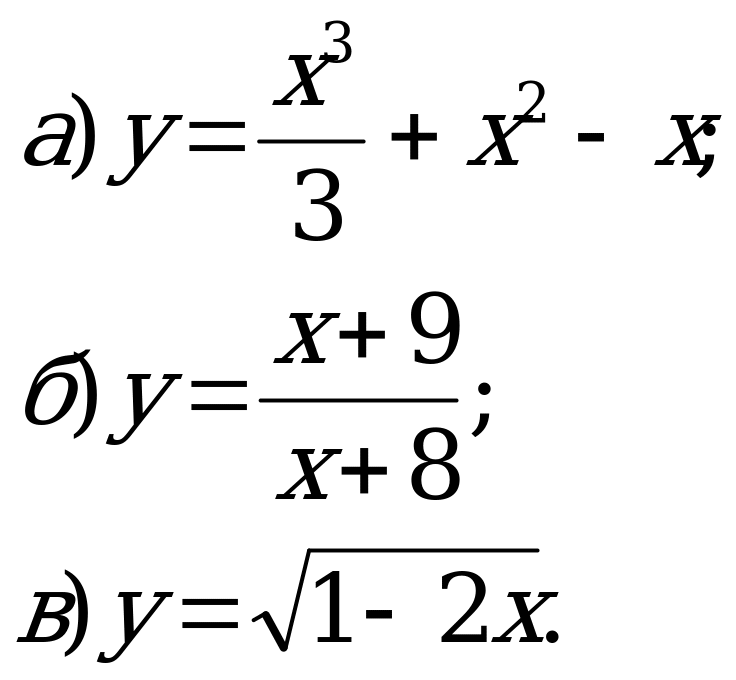 ренировочные упражнения: К графику заданной функции проведите касательную так, чтобы она была параллельна прямой y = 2 – x:
ренировочные упражнения: К графику заданной функции проведите касательную так, чтобы она была параллельна прямой y = 2 – x:









