Муниципальное автономное общеобразовательное учреждение "Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина"
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
по теме:
«Решение задач с параметром из ЕГЭ»
Выполнила:
Учащаяся 11 класса «А»
Кудрявцева Маргарита Викторовна
Подпись
Научный руководитель:
Сухненко И. А.,
учитель математики
Тамбов, 2018
| Оглавление |
|
| Введение | 3 |
| Глава 1. Основное о параметре | 5 |
| 1.1 Что такое параметр? | 5 |
| 1.2 Что означает «решить задачу с параметром»? | 5 |
| 1.3 Основные способы (методы) решения задач с параметром | 7 |
| 1.4 Решения некоторых задач указанными способами | 7 |
| Глава 2. Параметр в ЕГЭ 2018 года | 11 |
| 2.1 Функции, зависящие от параметра | 13 |
| 2.2 Уравнения с параметром | 15 |
| 2.3 Неравенства с параметром | 17 |
| 2.4 Системы с параметром | 20 |
| Заключение | 23 |
| Информационные ресурсы | 24 |
Введение.
В повседневной жизни мы очень часто сталкиваемся с понятием параметра: параметр загрузки в windows 8, параметры бытовых приборов, параметры автомобиля. Покупая какую-то вещь, мы внимательно изучаем ее основные характеристики. Так, приобретая компьютер, мы обращаем внимание на следующие его параметры: производительность, габариты, состав комплектующих, цену и др. Исследование многих жизненных процессов осуществляется с помощью параметров. Например, состояние больного определяется с помощью параметров температуры, давления. Для оценки состояния спортсмена в качестве параметра используется частота сердечных сокращений. Положение движущегося тела в пространстве определяется параметром времени. В изолированном сосуде данного объема давление газа характеризуется параметром температуры.
Толковый словарь определяет параметр как величину, характеризующую какое-нибудь основное свойство машины, устройства, системы или явления, процесса. (Ожегов С.И., Шведова Н.Ю. Толковый словарь русского языка. Москва. 1999). Рассмотрение параметров - это всегда выбор. Перед выбором мы стоим и в различных жизненных ситуациях.
Но что же собой представляет параметр в математике? Какую роль он играет при решении уравнений? Какими методами решаются уравнения с параметрами?
Актуальность данной темы определяется необходимостью уметь решать такие уравнения с параметрами при сдачи Единого Государственного экзамена и на вступительных экзаменах в высшие учебные заведения.
Цель данной работы систематизировать уравнения, содержащие параметр, и составить алгоритм их решения с учетом свойств различных функций.
Для достижения поставленной цели необходимо решить следующие задачи:
1) дать определения понятию «уравнение с параметрами»;
2) показать принцип решения данных уравнений на общих случаях;
3) показать решение задач с параметром из ЕГЭ, используя различные методы;
4) составить алгоритм решения задач с параметром из ЕГЭ, с учетом формулировки задания.
Для выполнения поставленной цели были использованы следующие методы: использование литературы разного типа, работа в группах на уроках алгебры и факультативных занятиях по математике.
Объектом исследовательской работы было решение уравнений с параметрами, связанных со свойствами выше представленных функций.
Я выбрала эту тему, так как она является неотъемлемой частью изучения школьного курса алгебры. Готовя данную работу, я ставила цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. Моя работа поможет понять другим ученикам как решаются уравнения с параметрами, применяя аналитический и графического методы, узнать о происхождении таких уравнений. В своей работе я ознакомилась с теоретическими основами решения уравнений, содержащих параметр. Рассмотрела аналитический и графический способы решения основных видов уравнений, содержащих параметр.
В моей работе рассмотрены часто встречающиеся типы уравнений, и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов, ведь уравнения с параметрами по праву считаются одними из самых сложных задач в курсе школьной математики. Именно такие задачи и попадают в список заданий на ЕГЭ.
Задачи с параметрами представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков. Они обладают диагностической ценностью, так как с помощью них можно проверить знание основных разделов математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности и перспективные возможности успешного овладения курса математики в высших учебных заведениях.
Глава 1. Основное о параметре
1.1 Что такое «параметр»?
Если в уравнении, помимо переменной x, есть переменная a и требуется решить это уравнение относительно x, считая переменную a постоянной, то данное уравнение будет называться уравнением с одной переменной x и параметром a.
Определение: параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Особенность уравнений с параметрами:
с одной стороны, параметр в уравнении следует считать величиной известной, а с другой — конкретное значение параметра не дано. С одной стороны, параметр является величиной постоянной, а с другой — может принимать различные значения. Получается, что параметр в уравнении — это «неизвестная величина», «переменная постоянная». Этот «каламбур» довольно точно отражает суть тех сложностей, которые встают перед теми, кто решает уравнения с параметром.
1.2 Что означает «решить задачу с параметром»?
Чаще всего в задачах содержится один параметр, хотя бывают случаи, когда параметров больше одного. Решить уравнение с параметром – значит указать для каждого значения параметра множество решений уравнения.
Самые простые задачи с параметром и их решения:
x/2=a = x=2a при любом a
ax=10 = x=10/a = x=10/a при a≠0
x=√a = x=√a при a≥0
2ax–4=0 = 2ax=4 = x=2/a = x=2/a при a≠0
|x|=a–1 = a–1≥0 = x=a–1 или x=1–a при a≥1
Основные типы задач с параметрами:
1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.
2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).
При решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы и совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Однако не стоит абсолютизировать сказанное, так как иногда прямое решение в соответствии с типом 1 является единственным разумным путем получения ответа при решении задачи типа 2.
3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).
Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.
4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Например, найти значения параметра, при которых:
1) уравнение выполняется для любого значения переменной из заданного промежутка;
2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.
1.3 Основные способы (методы) решения задач с параметром
Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения. Аналитический способ решения задач с параметром довольно трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).
Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.
1.4 Решения некоторых задач указанными способами
1 задача: Для всех действительных значений параметра a решите уравнение x3–(2–a)x2–ax–a(a–2)=0.
Решение: Исходное кубическое по x уравнение является квадратным относительно a. Поэтому, считая переменную x параметром, перепишем это уравнение в виде стандартного квадратного уравнения относительно a, опуская промежуточные шаги по раскрытию скобок и перегруппировке: –a2+(x2–x+2)a+x3–2x2 = 0.
Преобразуем: a2–(x2–x+2)a –x3 +2x2 =0. = x2–x+2=x2+(2–x) = –x3+2x2 =x2(2–x)
Легко заметить, что в первом случае можно увидеть сумму квадратов, а во втором их произведение. Поэтому по теореме, обратной теореме Виета получаем, что a1=x2, a2=2–x. Исходное уравнение преобразуется в совокупность из двух: a=x2 и a=2–x.
Из того, что x2=a следует, что:
1)при a
2)при a=0 решение будет всего одно, x=0
3)при a0 решений два, x=√a и x=–√a
Второе уравнение совокупности будет иметь 1 корень при любом a.
Комментарий 1. Многие учащиеся, доведя решение до данного момента, испытывают трудности в формировании общего ответа. Приведем удобный прием представления полученных результатов для дальнейшего продвижения в решении задачи. Будем называть данный прием: «разверткой вдоль оси параметра».
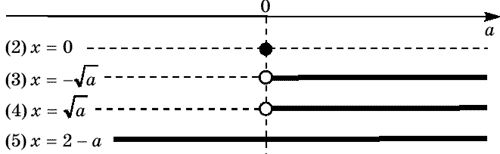 Изображаем ось параметра a и отмечаем на ней граничные значения параметра, которые фигурируют в ответах к каждому уравнению совокупности. Все найденные решения уравнений для тех значений параметра a, при которых хотя бы одно решение существует, выписываем в таблице слева (последовательно сверху вниз). Сплошной линией, параллельной оси параметра, указываем те промежутки значений параметра, при которых полученное решение существует. Заметим, что концы промежутков изображаются «светлыми» точками в случае, когда соответствующее решение не существует, а «темными» точками — в противном случае.
Изображаем ось параметра a и отмечаем на ней граничные значения параметра, которые фигурируют в ответах к каждому уравнению совокупности. Все найденные решения уравнений для тех значений параметра a, при которых хотя бы одно решение существует, выписываем в таблице слева (последовательно сверху вниз). Сплошной линией, параллельной оси параметра, указываем те промежутки значений параметра, при которых полученное решение существует. Заметим, что концы промежутков изображаются «светлыми» точками в случае, когда соответствующее решение не существует, а «темными» точками — в противном случае.
Таблица 1
Данная развертка позволяет легко найти все решения исходного уравнения для любого действительного значения параметра: x=2–a при a; x=0 или x=2 при a=0; x=–√a или x=√a или x=2–a при a0.
Можно увидеть, что при a=1 равенства x=2–a и x=√a принимают одинаковое значение x=1. Можно легко найти второй такой корень, приравняв x=2–a и x=–√a. Это будет x=–2 при a=4. Таким образом мы можем переписать ответ в более правильном виде: x=2–a при a1=0, x2=2 при a=0; x=√a, x=–√a и x=2–x при 0aaa4; x=1, x=–1 при a=1; x=2, x=–2 при a=4.
2 задача: При каких a уравнение |x2+2x–3|–2a=|x–a|+3 имеет ровно три корня?
Решение: Используем графический метод решения. График функции y=|x2+2x–3| отличается от параболы y=x2+2x–3 только тем, что отрицательная ее область зеркально отражается вверх относительно оси OX (ведь модуль не может принимать отрицательных значений). График функции y=|x–a|+2a+3 представляет собой всем известную «галочку», вершина которой смещена в точку (a;2a+3). В зависимости от значений параметра возможны следующие варианты взаимного расположения этих графиков на координатной плоскости: 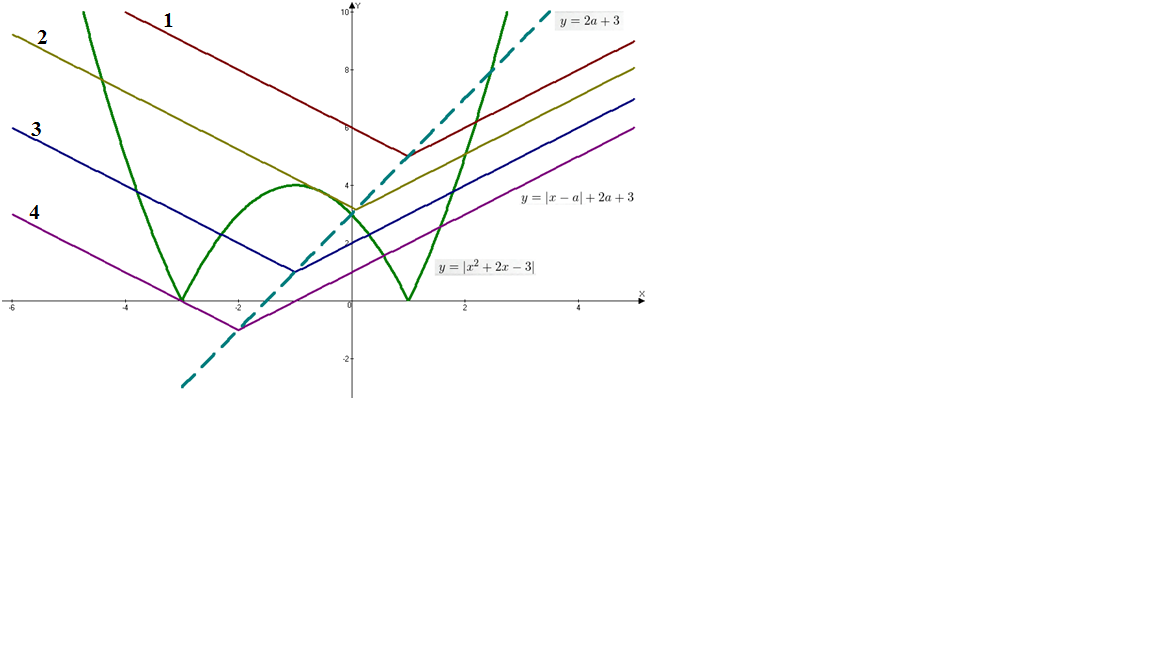
Видно, что три решения уравнение будет в случаях 2 и 4. Первый случай выполняется при условии выполнения равенства 0=|-3-a|+2a+3, следовательно a=–2.
Во втором случае оба модуля раскрываются с отрицательным знаком. Этот случай выполняется при условии, что дискриминант квадратного уравнения x2+x+3a=0 равен нулю, то есть при a=1/12.
Таким образом получается, что ответ на вопрос при каких a данное уравнение имеет ровно три корня такой: при a=–2 и a=1/12.
3 задача: При каких значениях параметра a уравнение 52x-3*5x+a-1=0 имеет единственный корень?
Решение: Сделаем замену 5x=t, t0. Тогда наше уравнение будет иметь вид:
t2-3*t+a-1=0. Это уравнение будет иметь 1 корень в двух случаях:
1)Если дискриминант будет равен 0
2)Если дискриминант будет больше нуля, но один из корней будет отрицательным
Рассмотрим эти случаи.
D=9-4a+4=13-4a=0
Отсюда получаем a=13/4 – первый подходящий корень.
2) D=13-4a
Тогда корни будут такие:
t=(3+√(13-4a))/20
t=(3-√(13-4a))/2≤0
Возьмем первый корень положительным, а второй наоборот. В таком случае условие единственного ответа будет выполнено.
Решая неравенство t=(3+√(13-4a))/20 получаем, что a≤1. Значит в ответ нужно записать, что aЄ(-∞;1]U{13/4}
Глава 2. Параметр в ЕГЭ 2018 года
Чтобы решить задание 18 по математике профильного уровня нужно знать:
Задание 18 в ЕГЭ подразделяется на несколько видов:
1) функции, зависящие от параметра;
2) уравнения с параметрами;
3) неравенства с параметрами;
4) системы и неравенства с параметрами.
Пусть задано уравнение f(x;a)=0, которое следует решить относительно переменной х, а произвольное действительное число обозначено буквой а, то f(x;a)=0 – это уравнение с параметром а.
Решить неравенство с параметром - это значит исследовать каким будет решение неравенства для всех возможных значений параметра.
Решить уравнение с параметром – это значит найти все значения параметров, при которых данное уравнение имеет решение.
Линейные уравнения с параметрами — общий вид ax=b, где a, b – параметры.
Обратите внимание: для данного вида уравнения контрольным значением параметра является то значение, при котором обращается в нуль коэффициент при неизвестном.
При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.
Особым значением параметра а является значение а=0.
1)Если а≠0, то при любой паре параметров а и b оно
имеет единственное решение .
2)Если а=0, то уравнение принимает вид 0х=b. В этом случает значение b=0 является особым значением параметра b.
3)При b≠0 уравнение решений не имеет.
4)При b=0 уравнение примет вид:0х=0. Решением данного уравнения является любое действительное число.
Дробно-рациональные уравнения с параметрами, сводящиеся к линейным.
При решении данного типа уравнений следует дробное уравнение заменить целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. Далее следует решать уравнение по известному алгоритму, исключив посторонние корни, т. е. те числа, которые обращают общий знаменатель в ноль (решить уравнения относительно параметра).
Показательные уравнения с параметрами
Многие показательные уравнения с параметрами сводятся к
элементарным показательным уравнениям вида аf (x) = bφ(х) (1), где а 0, b 0.
ОДЗ такого уравнения находится как пересечение областей
допустимых значений функций f(x) и φ(х).
Для решения уравнения (1) нужно рассмотреть следующие
случаи:
1)При a=b=1 решением уравнения (1) является область его допустимых значений D.
2)При а=1, b≠1 решением уравнения (1) служит решение уравнения φ(х)=0 на области допустимых значений D.
3)При а≠1, b=1 решением уравнения (1) служит решение уравнения f(х)=0 на области допустимых значений D.
4)При a=b (a0, a≠1, b0, b≠1) уравнение (1) равносильно уравнению f(x)=φ(х) на области D.
5)При a≠b (a0, a≠1, b0, b≠1) уравнение (1) тождественно уравнению на области D.
2.1 Функции, зависящие от параметра
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения a, при каждом из которых наибольшее значение функции f(x)=|x-a|-x² не меньше 1. (Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
Решение: Чтобы наибольшее значение данной функции было не меньше 1, необходимо и достаточно, чтобы она в какой-то точке приняла значение 1. Поэтому можно сказать, что |x-a|-x²≥1. В зависимости от переменной a это неравенство равносильно системе неравенств:
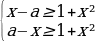
Решая эти неравенства получаем 2 дискриминанта:
D=-3-4a и D=-3+4a. Неравенства будут иметь решения, если эти дискриминанты неотрицательны. Решая -3-4a≥0 и -3+4a≥0 получаем, что a≤-3/4 и a≥3/4.
Ответ: aЄ(-∞;-3/4]U[3/4;+∞).
2 задача: Найти все значения параметра a, при каждом из которых среди значений функции y=(x²-2x+a)/(6+x²) есть ровно одно целое число.(Источник: МИОО: Тренировочная работа по математике 2010 год вариант 501. (Часть С))
Решение: Функция определена и непрерывна на всей числовой прямой. Уравнение (x²-2x+a)/(6+x²)=1 при любом a имеет решение x=(a-6)/2. Значит, при любом a одно из значений функции равно 1.
Поскольку функция непрерывна, множество её значений образует промежуток, включающий число 1. Других целых значений функции нет, если для всех x:
0(x²-2x+a)/(6+x²).
Это равносильно системе неравенств:
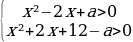
Чтобы неравенства выполнялись для всех x дискриминанты обоих трёхчленов должны быть отрицательны, следовательно: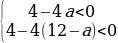
Ответ: aЄ(1;11).
3 задача: Найдите все значения a, при каждом из которых наименьшее значение f(x)=4x²-4ax+a²+2a+2 на множестве |x|≥1 не меньше 6.(Источник: Портал РешуЕГЭ задание 500471)
Решение: Графиком функции f(x)=4x²-4ax+a²+2a+2 является парабола, ветви которой направлены вверх, а вершина имеет координаты (a/2;2a+2).
Значит, минимум функции f(x) на всей числовой оси достигается при x=a/2.
На множестве |x|≥1 эта функция достигает наименьшего значения либо в точке x=a/2, если эта точка принадлежит множеству, либо в одной из граничных точек x=±1.
Если наименьшее значение функции не меньше 6, то и всякое значение функции не меньше 6. В частности,
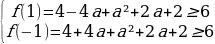
Упрощая, получаем систему неравенств:
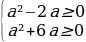
Решая эту систему, получаем значения a:
a€(-∞;-6]U{0}U[2;+∞).
Но нам подходят не все данные корни. Сделаем отбор корней.
1) Если a≤-6, то a/2≤-3 значит, наименьшее значение функции достигается в точке a/2 и f(a/2)=2a+2=-10, что не удовлетворяет условию задачи.
2) Если a=0, то a/2=0, значит, наименьшее значение функции достигается в одной из граничных точек x=±1, в которых значение функции не меньше 6.
3)Если a≥2, то a/2≥1, значит, наименьшее значение функции достигается в точке x=a/2 и f(a/2)=2a+2≥6, что удовлетворяет условию задачи.
Ответ: a=0, a≥2.
2.2 Уравнения с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения a, при каждом из которых уравнение 64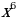 -
-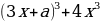 -3x=a имеет более одного корня.(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
-3x=a имеет более одного корня.(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
Решение: Преобразуем уравнение 64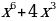 =
=
=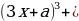 +a).
+a).
Рассмотрим функцию f(x)=t³+t. Она монотонно возрастает как сумма двух возрастающих функций. Поэтому уравнение f(4x²)=f(3x+a) равносильно уравнению 4x²=3x+a. Оно имеет более одного корня в тех случаях, когда дискриминант уравнения 4x²-3x-a=0 положителен. То есть когда 9+16a0, a-9/16.
Ответ: a-9/16.
2 задача: Найдите все значения a, при каждом из которых модуль разности корней уравнения x²-6x+12+a²-4a=0 принимает наибольшее значение.(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
Решение: По теореме Виета получаем, что 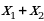 =6 и
=6 и 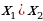 =12+a²-4a. Отсюда получается, что искомая разность равна |
=12+a²-4a. Отсюда получается, что искомая разность равна |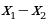 |=
|=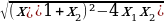 =
=
=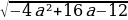
Следовательно, нужно только найти наибольшее значение выражения 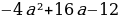 = -4(a-2)²+4. Оно будет равно 4 и будет достигаться при a=2. Следовательно, наибольшая разность корней будет равна √4=2.
= -4(a-2)²+4. Оно будет равно 4 и будет достигаться при a=2. Следовательно, наибольшая разность корней будет равна √4=2.
Ответ: a=2. При этом модуль разности корней равен 2.
3 задача: Найдите все значения а, при каждом из которых уравнение 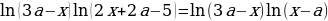 имеет ровно один корень на отрезке [0; 2].(Источник: Задание 18 (С6) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 401 (C часть))
имеет ровно один корень на отрезке [0; 2].(Источник: Задание 18 (С6) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 401 (C часть))
Решение: Имеем уравнение вида ab=ac, откуда на ОДЗ либо a=0, либо b=c. Рассмотрим эти 2 случая:
Первый случай:
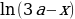 =0 при условиях:
=0 при условиях: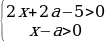
Имеем такую систему:
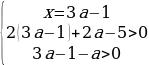
Упрощая эти неравенства, получаем:
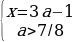
Число 3a-1 лежит на отрезке [0;2], если 1/3≤a≤1. Тогда для первого случая получаем: 7/8a≤1.
Второй случай:
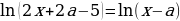 при условии, что 3a-x0. Получаем:
при условии, что 3a-x0. Получаем:
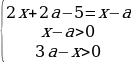
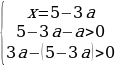
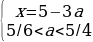
Число x=5-3a лежит на отрезке [0;2], если 1≤a≤5/3. Тогда для второго случая получаем: 1≤a≤5/4.
Корень x=5-3a равен x=3a-1, если a=1.
Значит исходное уравнение имеет ровно один корень на отрезке [0;2] при 7/8a.
Ответ: aЄ(7/8;5/4).
2.3 Неравенства с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения параметра а, при каждом из которых множество решений неравенства 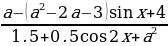 содержит отрезок [-2
содержит отрезок [-2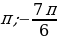 ].(Источник: Задание 18 (Сб) ЕГЭ 2015)
].(Источник: Задание 18 (Сб) ЕГЭ 2015)
Решение: Заметим, что при любых значениях переменной x и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству
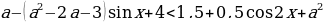
Для того, чтобы множество решений неравенства содержало отрезок [-2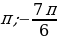 ] синус должен принимать значения 0≤
] синус должен принимать значения 0≤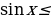 1. Пусть
1. Пусть 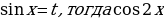 =1-2t² и неравенство принимает вид
=1-2t² и неравенство принимает вид
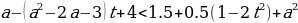 t²-(a²-2a-3)t-a²+a+2
t²-(a²-2a-3)t-a²+a+2
Введем функцию: f(t)= t²-(a²-2a-3)t-a²+a+2
Для того, чтобы выполнялось наше условие, необходимо и достаточно, чтобы одновременно выполнялись 2 условия: f(0)f(1)

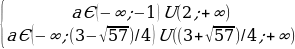
Пересечение этих промежутков и будет ответом.
Ответ: aЄ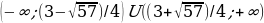
2 задача: Найдите все значения параметра а, при каждом из которых неравенство |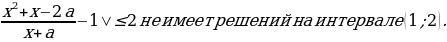 (Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 1. (Часть C))
(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 1. (Часть C))
Решение: Преобразуем исходное неравенство, приведя левую часть к одному знаменателю: |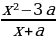 |≤2
|≤2 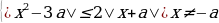
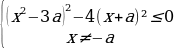
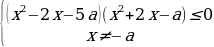
Р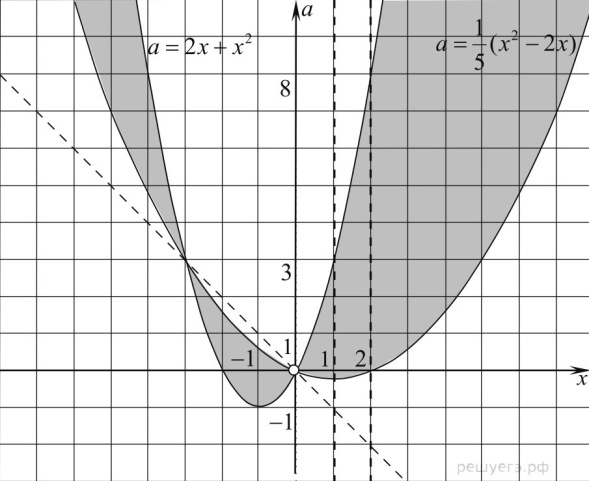 ешим неравенство на интервале (1;2):
ешим неравенство на интервале (1;2):
a≤-1/5:пустое множество
-1/5a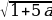 ]
]
0≤a≤3: (1;2)
3a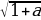 ;2)
;2)
a≥8: пустое множество
Ответ: aЄ(-∞;-1/5]U[8;+∞).
3 задача: Найдите все значения a , при каждом из которых неравенство |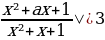 выполняется при всех x.(Источник: Портал РешуЕГЭ задание 500115)
выполняется при всех x.(Источник: Портал РешуЕГЭ задание 500115)
Решение: Поскольку знаменатель левой части больше нуля при любом x, получаем: |x²+ax+1|x²+3x+3.
Решим полученное неравенство:
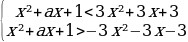
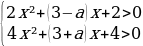
Чтобы любое значение x удовлетворяло этой системе неравенств, дискриминанты левых частей должны быть отрицательными:
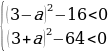
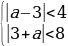
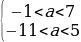 -1.
-1.
Ответ: aЄ(-1;5).
2.4 Системы с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения параметра a, при каждом из которых система неравенств 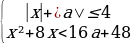 имеет хотя бы одно решение на отрезке [-1;0].( Источник: ЕГЭ по математике — 2017. Досрочная волна, резервный день, вариант А. Ларина (часть С))
имеет хотя бы одно решение на отрезке [-1;0].( Источник: ЕГЭ по математике — 2017. Досрочная волна, резервный день, вариант А. Ларина (часть С))
Решение: Преобразуем систему:
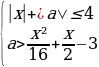
Первое неравенство задает на плоскости xOa квадрат, ограниченный отрезками прямых a=x+4, a=x-4, a=-x-4, a=- x+4, а неравенство 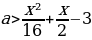 задает часть плоскости внутри параболы с вершиной (-4;-4), ветви которой направлены вверх. Найдем координаты точки А пересечения параболы с прямой a=-x-4:
задает часть плоскости внутри параболы с вершиной (-4;-4), ветви которой направлены вверх. Найдем координаты точки А пересечения параболы с прямой a=-x-4:
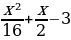 = -x-4
= -x-4 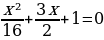 x²+24x+16=0 x=-12±8√2
x²+24x+16=0 x=-12±8√2
М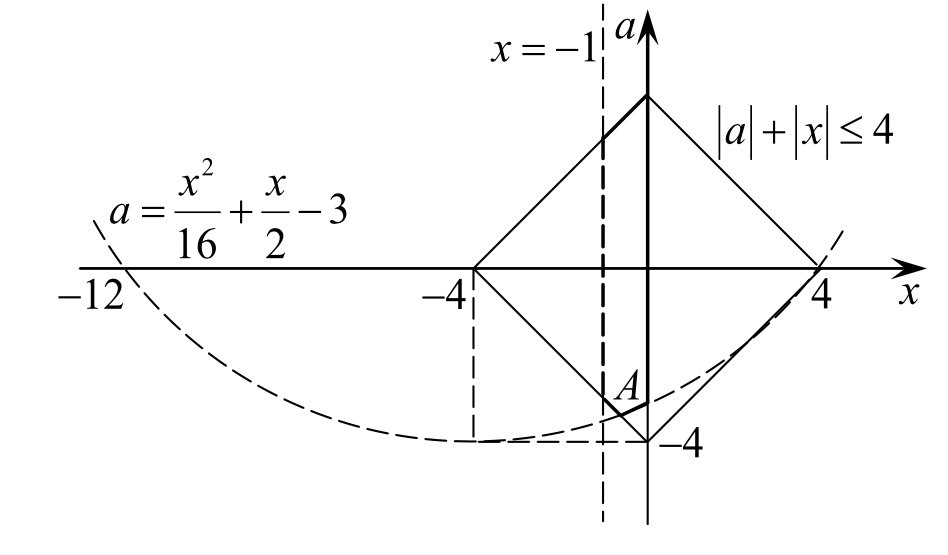 еньший корень -12-8√2x=-1 и x=0. Тогда искомыми являются значения параметра, большие ординаты точки А, но не большие 4. Имеем: a=-(-12+8√2)-4=8-8√2.
еньший корень -12-8√2x=-1 и x=0. Тогда искомыми являются значения параметра, большие ординаты точки А, но не большие 4. Имеем: a=-(-12+8√2)-4=8-8√2.
Тогда система будет иметь решения при 8-8√2≤a≤4.
Ответ: aЄ[8-8√2;4].
2 задача: Найдите все неотрицательные значения a , при каждом из которых система уравнений  имеет единственное решение.( Источник: СтатГрад: Тренировочная работа по математике 27.04.2016 вариант МА10509)
имеет единственное решение.( Источник: СтатГрад: Тренировочная работа по математике 27.04.2016 вариант МА10509)
Решение: Первому уравнению системы удовлетворяют те и только те точки (x;y), которые лежат на отрезке AB прямой, соединяющей точки A(-2;0) и B(0;a), где a≥0, поскольку уравнение задаёт множество точек (x;y), сумма расстояний от каждой из которых до точек А и В равна 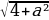 , что равно длине отрезка АВ.
, что равно длине отрезка АВ.
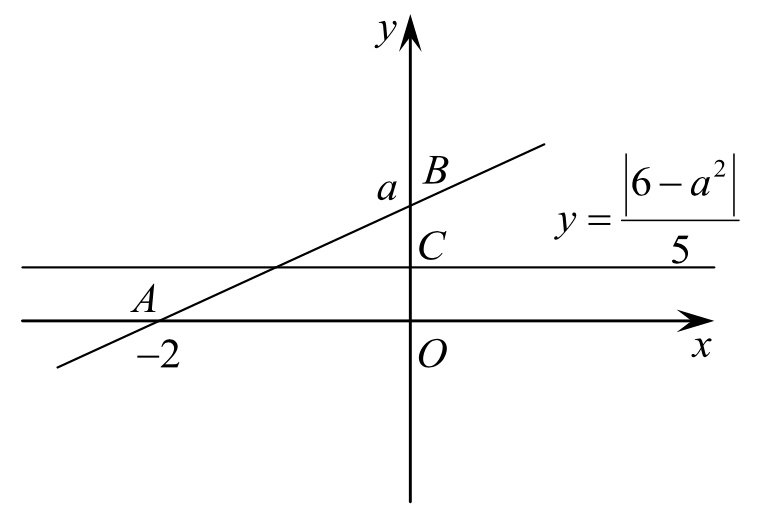 Второму уравнению системы удовлетворяют те и только те точки (x;y), которые лежат на прямой y=
Второму уравнению системы удовлетворяют те и только те точки (x;y), которые лежат на прямой y= параллельной оси абсцисс и проходящей через точку С(0;
параллельной оси абсцисс и проходящей через точку С(0;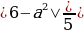 .
.
Отсюда следует, что условие задачи выполнено тогда и только тогда, когда точка С лежит между точками О и В, причём если точка С совпадает с точкой А или с точкой В, то условие задачи выполнено.
Решим неравенство 0≤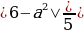 ≤a. Получается, что 1≤a≤6.
≤a. Получается, что 1≤a≤6.
Ответ: aЄ[1;6].
3 задача: Найдите все значения параметра a, при каждом из которых система уравнений 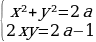 имеет ровно два решения.(Источник: Портал РешуЕГЭ задание 484630)
имеет ровно два решения.(Источник: Портал РешуЕГЭ задание 484630)
Решение: Заменим первое уравнение разностью, а второе – суммой исходных уравнений: 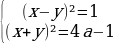 .
.
При a система решений не имеет. При a≥1/4 получаем:
y=x-1 или y=x+1
y=- x-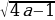 или y= -x+
или y= -x+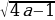
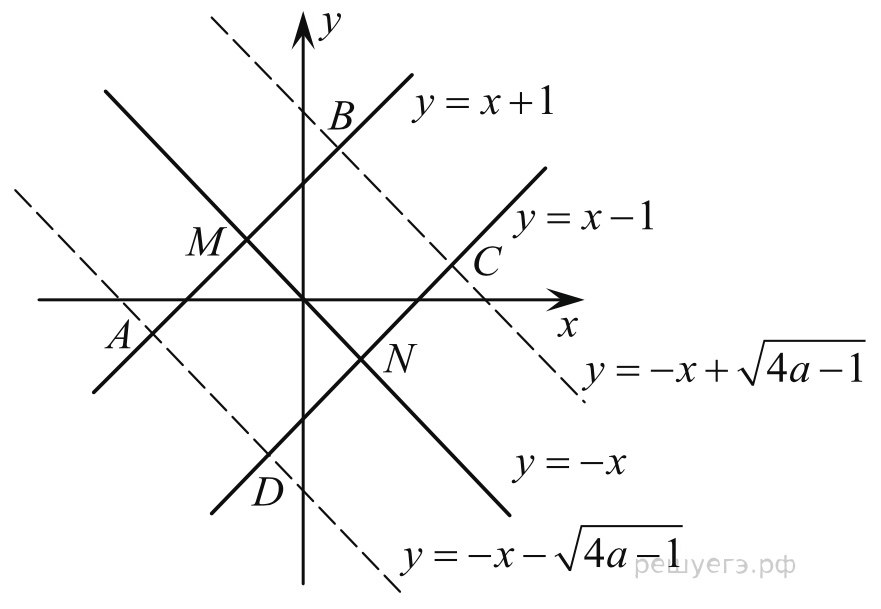
Ясно (см. рисунок), что при a1/4 система имеет четыре решения (координаты точек A, B, C и D), а при a=1/4 — два решения (координаты точек M и N).
Ответ: a=1/4.
Заключение
Работа над данной темой была интересной и познавательной. Изучив методы решения уравнений с параметрами, я обогатила свой опыт:
• новыми научными понятиями;
• узнала методы, которые выходят за рамки школьной программы;
• углубила и расширила свои знания.
Изучив данную тему, можем сделать вывод. Параметр – это буква, которая «никому ничем не обязана» и может принимать любые допустимые значения. Структура решений уравнения зависит от значений параметра; те или иные аспекты этой зависимости и предстоит выяснять в каждой конкретной задаче. Для этого нужно использовать различные формы и методы решения, с учетом свойств каждой конкретной функции.
Рассмотрев конкретные задачи, я пришла к выводу, что нужно уметь правильно видеть, какой метод решения подходит в той или иной ситуации, чтобы не тратить время, бесполезно решая задачу не тем способом. Именно это - научиться видеть, какой метод решения будет лучше в том или ином примере – является одной из целей проекта.
Эта работа поможет мне в сдаче ЕГЭ. Работа над проектом позволила приобрести опыт выполнения научной работы.
Информационные ресурсы:
https://yourtutor.info/%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B7%D0%B0%D0%B4%D0%B0%D1%87-%D1%81-%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80%D0%B0%D0%BC%D0%B8-%D0%B8%D0%B7-%D0%B5%D0%B3%D1%8D/comment-page-1#comment-9319
https://bingoschool.ru/ege/maths-profile/tasks/18/#main
https://ege.sdamgia.ru/test?a=catlistwstat
Учебно-метадическое пособие «Задачи с параметрами» авторов И.Ю.Ивановой и С.В.Казадаева; «Задачи с параметрами в ЕГЭ» А.Х.Шахмейстер; интернет-ресурсы







 Изображаем ось параметра a и отмечаем на ней граничные значения параметра, которые фигурируют в ответах к каждому уравнению совокупности. Все найденные решения уравнений для тех значений параметра a, при которых хотя бы одно решение существует, выписываем в таблице слева (последовательно сверху вниз). Сплошной линией, параллельной оси параметра, указываем те промежутки значений параметра, при которых полученное решение существует. Заметим, что концы промежутков изображаются «светлыми» точками в случае, когда соответствующее решение не существует, а «темными» точками — в противном случае.
Изображаем ось параметра a и отмечаем на ней граничные значения параметра, которые фигурируют в ответах к каждому уравнению совокупности. Все найденные решения уравнений для тех значений параметра a, при которых хотя бы одно решение существует, выписываем в таблице слева (последовательно сверху вниз). Сплошной линией, параллельной оси параметра, указываем те промежутки значений параметра, при которых полученное решение существует. Заметим, что концы промежутков изображаются «светлыми» точками в случае, когда соответствующее решение не существует, а «темными» точками — в противном случае. 
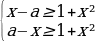
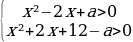
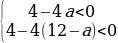
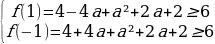
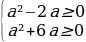
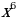 -
-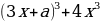 -3x=a имеет более одного корня.(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
-3x=a имеет более одного корня.(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)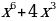 =
=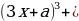 +a).
+a).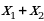 =6 и
=6 и 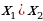 =12+a²-4a. Отсюда получается, что искомая разность равна |
=12+a²-4a. Отсюда получается, что искомая разность равна |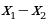 |=
|=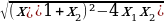 =
=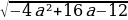
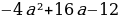 = -4(a-2)²+4. Оно будет равно 4 и будет достигаться при a=2. Следовательно, наибольшая разность корней будет равна √4=2.
= -4(a-2)²+4. Оно будет равно 4 и будет достигаться при a=2. Следовательно, наибольшая разность корней будет равна √4=2.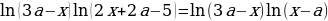 имеет ровно один корень на отрезке [0; 2].(Источник: Задание 18 (С6) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 401 (C часть))
имеет ровно один корень на отрезке [0; 2].(Источник: Задание 18 (С6) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 401 (C часть))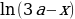 =0 при условиях:
=0 при условиях: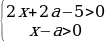
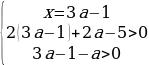
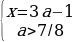
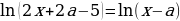 при условии, что 3a-x0. Получаем:
при условии, что 3a-x0. Получаем: 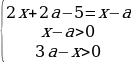
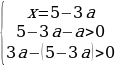
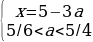
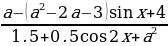 содержит отрезок [-2
содержит отрезок [-2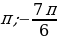 ].(Источник: Задание 18 (Сб) ЕГЭ 2015)
].(Источник: Задание 18 (Сб) ЕГЭ 2015)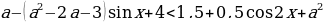
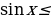 1. Пусть
1. Пусть 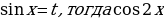 =1-2t² и неравенство принимает вид
=1-2t² и неравенство принимает вид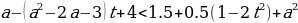 t²-(a²-2a-3)t-a²+a+2
t²-(a²-2a-3)t-a²+a+2
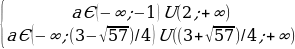
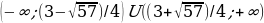
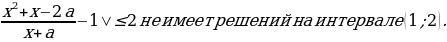 (Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 1. (Часть C))
(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 1. (Часть C))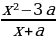 |≤2
|≤2 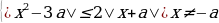
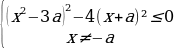
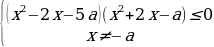
 ешим неравенство на интервале (1;2):
ешим неравенство на интервале (1;2):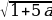 ]
]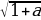 ;2)
;2)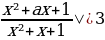 выполняется при всех x.(Источник: Портал РешуЕГЭ задание 500115)
выполняется при всех x.(Источник: Портал РешуЕГЭ задание 500115)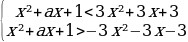
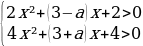
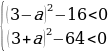
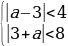
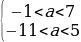 -1.
-1.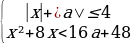 имеет хотя бы одно решение на отрезке [-1;0].( Источник: ЕГЭ по математике — 2017. Досрочная волна, резервный день, вариант А. Ларина (часть С))
имеет хотя бы одно решение на отрезке [-1;0].( Источник: ЕГЭ по математике — 2017. Досрочная волна, резервный день, вариант А. Ларина (часть С)) 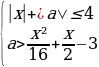
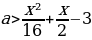 задает часть плоскости внутри параболы с вершиной (-4;-4), ветви которой направлены вверх. Найдем координаты точки А пересечения параболы с прямой a=-x-4:
задает часть плоскости внутри параболы с вершиной (-4;-4), ветви которой направлены вверх. Найдем координаты точки А пересечения параболы с прямой a=-x-4: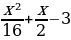 = -x-4
= -x-4 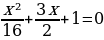 x²+24x+16=0 x=-12±8√2
x²+24x+16=0 x=-12±8√2  еньший корень -12-8√2x=-1 и x=0. Тогда искомыми являются значения параметра, большие ординаты точки А, но не большие 4. Имеем: a=-(-12+8√2)-4=8-8√2.
еньший корень -12-8√2x=-1 и x=0. Тогда искомыми являются значения параметра, большие ординаты точки А, но не большие 4. Имеем: a=-(-12+8√2)-4=8-8√2. имеет единственное решение.( Источник: СтатГрад: Тренировочная работа по математике 27.04.2016 вариант МА10509)
имеет единственное решение.( Источник: СтатГрад: Тренировочная работа по математике 27.04.2016 вариант МА10509)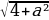 , что равно длине отрезка АВ.
, что равно длине отрезка АВ.  Второму уравнению системы удовлетворяют те и только те точки (x;y), которые лежат на прямой y=
Второму уравнению системы удовлетворяют те и только те точки (x;y), которые лежат на прямой y= параллельной оси абсцисс и проходящей через точку С(0;
параллельной оси абсцисс и проходящей через точку С(0;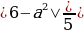 .
.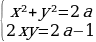 имеет ровно два решения.(Источник: Портал РешуЕГЭ задание 484630)
имеет ровно два решения.(Источник: Портал РешуЕГЭ задание 484630)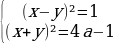 .
.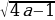 или y= -x+
или y= -x+










