Решение задач с помощью дробно рациональных уравнений

Решение задач с помощью дробных рациональных уравнений

Цель: рассмотреть типы задач, решаемых с помощью дробных рациональных уравнений, понятие математической модели и этапы решения задачи.

Повторение пройденного материала

• Назовите дробные рациональные уравнения:

Повторение пройденного материала

• Назовите общий знаменатель дробей, входящих в уравнения:

Повторение пройденного материала

• Назовите порядок решения дробных рациональных уравнений.

• Найти общий знаменатель дробей, входящих в уравнение.
• Умножить обе части уравнения на общий знаменатель.
• Решить получившееся целое уравнение.
• Исключить из его корней те, которые обращают в нуль общий знаменатель.

• Записать ответ.

Понятие математической модели

• Представление реальной ситуации на языке математики с использованием различных правил, свойств и законов математики называется математической моделью задачи .

• Различают несколько видов математических моделей:

• алгебраическая модель;
• графическая модель;
• геометрическая модель.

Этапы решения задачи

Первый этап. Составление математической модели.

Вводится переменная, текст задачи переводится на математический язык, составляется уравнение.

Второй этап. Работа с математической моделью.

Решение уравнения.

Третий этап. Ответ на вопрос задачи.

Анализируя полученное решение, записывается ответ на вопрос задачи.

Задачи, приводящие к решению дробных рациональных уравнений

Задачи, в которых одна величина выражается через другие при помощи дробного выражения:

• Задачи на движение:

• Задачи на работу:

Поезд опаздывал на 1 час, и чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию.

• Первый этап . Составление математической модели.

Занесём данные задачи в таблицу:

Так как время движения по расписанию на 1 час больше фактического, то составим уравнение:

S

V

t

720 км

ч

По расписанию

x км/ч

x+10 км/ч

Фактически

720 км

ч

Поезд опаздывал на 1 час, и чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию.

• Второй этап. Работа с математической моделью.

Решим уравнение:

При данных значениях x знаменатели дробей не равны нулю, значит эти значения - корни составленного уравнения.

Поезд опаздывал на 1 час, и чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию.

• Третий этап. Ответ на вопрос задачи.

Так как скорость поезда не может выражаться отрицательным числом, то значение не подходит условию задачи.

– скорость поезда по расписанию.

Ответ: 80 км/ч.

На изготовление 40 деталей первый рабочий тратит на 2 часа больше, чем второй на изготовление 36 деталей. Сколько деталей в час делает первый рабочий, если известно, что второй за час делает на 1 деталь больше?

• Первый этап . Составление математической модели.

Занесём данные задачи в таблицу:

Так как первый рабочий на выполнение работы тратит на 2 часа больше, то составим уравнение:

работа

производительность (дет/час)

время

1-ый рабочий

40

x

x+1

2-ой рабочий

36

На изготовление 40 деталей первый рабочий тратит на 2 часа больше, чем второй на изготовление 36 деталей. Сколько деталей в час делает первый рабочий, если известно, что второй за час делает на 1 деталь больше?

• Второй этап. Работа с математической моделью.

Решим уравнение:

При данных значениях x знаменатели дробей не равны нулю, значит эти значения - корни составленного уравнения.

На изготовление 40 деталей первый рабочий тратит на 2 часа больше, чем второй на изготовление 36 деталей. Сколько деталей в час делает первый рабочий, если известно, что второй за час делает на 1 деталь больше?

• Третий этап. Ответ на вопрос задачи.

Так как производительность не может выражаться отрицательным числом, то значение не подходит условию задачи.

деталей в час делает первый рабочий.

Ответ: 5 деталей.

Составьте математические модели задач

• С автобусной станции выехал автобус до железнодорожного вокзала, находящемся на расстоянии 40 км. Один из пассажиров автобуса опоздал к отправлению автобуса, и поехал на железнодорожный вокзал на такси, через 10 минут после автобуса. Автобус и такси приехали на железнодорожный вокзал одновременно. Известно также, что скорость такси на 20 км/ч больше скорости автобуса. Необходимо найти скорость такси и скорость автобуса.

S

V

t

автобус

такси

Составьте математические модели задач

• Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 часа. Какова скорость течения реки?

S

V

t

По течению

Против течения

Составьте математические модели задач

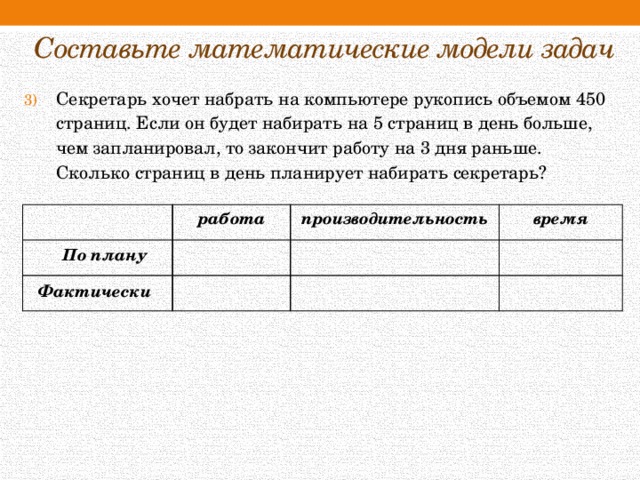
• Секретарь хочет набрать на компьютере рукопись объемом 450 страниц. Если он будет набирать на 5 страниц в день больше, чем запланировал, то закончит работу на 3 дня раньше. Сколько страниц в день планирует набирать секретарь?

работа

производительность

время

По плану

Фактически

Подведём итоги

• Какие задачи решаются с помощью дробных рациональных уравнений?
• Дайте понятие математической модели задачи.
• Какие типы математических моделей были использованы при решении задач?
• Назовите этапы решения задач.

Задание на самоподготовку

• Закончить решение задач 1, 2, 3.