Дата
Тема урока: Решение задач с помощью систем уравнений. Подготовка к контрольной работе
Задачи: познакомить учащихся с решением задач с помощью систем уравнений, формировать умение составлять систему уравнений по условию задачи и вспомнить методы решения систем уравнений.
Ход урока
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Выполните устно. Составить уравнение, зная, что:
а) величина одного угла треугольника — х градусов, величина другого угла — у градусов, а третий угол равен 30°;
б) за покупку 4 карандашей стоимостью х рублей каждый и 3 тетрадей стоимостью у рублей каждая заплатили 70 рублей;
в) сумма двух чисел равна 35.
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Открываем тетради, записываем сегодняшнее число и тему урока. Далее изучаем конспект и выполняем соответствующие записи.
Мы уже умеем решать задачи с помощью линейных уравнений с одной неизвестной. Сегодня мы научимся по условию задачи составлять систему уравнений с двумя неизвестными и находить ее решение.
Алгоритм решения задач с помощью систем уравнений:
а) обозначают некоторые неизвестные числа буквами и, используя условие задачи, составляют систему уравнений;
б) решают систему уравнений;
в) возвращаясь к условию задачи и использованным обозначениям, истолковывают результат, записывают ответ.
Пример 1. В трех тетрадях и четырех блокнотах вместе 108 страниц. В двух блокнотах столько же страниц, сколько их в трех тетрадях. Сколько страниц в каждой тетради и в каждом блокноте?
Решение.
Пусть х – количество страниц в каждой тетради, а у – количество страниц в каждом блокноте. Тогда в трех тетрадях 3х страниц, а в четырех блокнотах 4у страниц. По условию задачи общее количество страниц в этих тетрадях и блокнотах равно 108. Поэтому получаем первое уравнение:
3х + 4у = 108.
В двух блокнотах 2у страниц, в трех тетрадях 3х страниц. По условию задачи эти количества страниц равны. Тогда имеем второе уравнение:
2у = 3х.
Итак, получили систему двух линейных уравнений с двумя неизвестными:

Решим ее любым удобным для нас способом, например, способом подстановки. Обратим внимание, что в каждом уравнении системы участвует слагаемое «3х». Поэтому второе уравнение задает подстановку, которую необходимо применить к первому уравнению. Получаем

Необходимо найти теперь значение переменной «х». Подставим во второе уравнение  , получим:
, получим:

Вернемся к началу задачи и вспомним обозначения. Итак, в тетради 12 страниц, а в блокноте 18 страниц.
Ответ: в тетради 12 страниц, а в блокноте 18 страниц.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Открываем учебник на стр. 220 и выполняем письменно следующие номера.
№ 1099. Читайте условие в учебнике.
Оформим задачу с помощью таблицы, в которой определим неизвестные:
| Площадь под гречиху | x га |
|
| Площадь под просо | y га |
|
| Сумма площадей | (х + у) га | 19 га |
| Разница площадей | (х - у) га | 5 га |
По условию задачи составим систему уравнений:

Решим ее способом сложения, оставив без изменения первое уравнение:

Ответ: под гречиху 12 га, под просо 7 га.
№1100. Читайте условие в учебнике.
Оформим задачу с помощью таблицы, в которой определим неизвестные:
| В январе | x шт. |
|
| В феврале | y шт. |
|
| Всего изделий | (х + у) шт. | 1315 шт. |
| Разница изделий | (у - х) шт. | 165 шт. |
По условию задачи составим систему уравнений:

Решим ее способом подстановки, чтобы повторить и этот метод решения систем. Для этого выразим из второго уравнения у и подставим его выражение в первое уравнение:
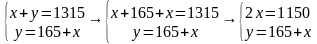

Ответ: в январе 575 штук, в феврале 740 штук.
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание: выучите новую теорию и выполните № 1101, 1103.









 , получим:
, получим: