План-конспект урока
Геометрия 9 класс
Глава 2. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Тема: «Решение треугольников»
Цель: сформулировать теорему синусов и теорему косинусов, организовать деятельность по осознанию обучающимися алгоритма применения этих теорем при решении задач; выделять существенные признаки при решении задач; развивать практические умения и навыки при выполнении вычислений, анализировать полученную информацию; способствовать формированию и развитию познавательного интереса учащихся к обучению.
Тип урока: комбинированный
Оборудование: компьютер, проектор.
Дидактическое сопровождение: карточки с формулами.
Планируемый результат:
1. Предметные: формулируют и записывают формулы;
освоение алгоритма решения задач по образцу, в общем виде.
2. Метапредметные:
регулятивные: преобразуют практическую задачу в познавательную, планируют собственную деятельность; осуществляют контроль и оценку своих действий;управление своей деятельностью на уроке; совместное с учителем и одноклассниками действия учащихся;
познавательные: проводят наблюдение, анализ; выдвигают предположения (моделируют процессы) и осуществляют их экспериментальную проверку; совместная (групповая) работа, выполняемая под руководством учителя;
коммуникативные:обмениваются знаниями между членами группы для принятия эффективных решений; навыки сотрудничества.
3. Личностные: проявляют устойчивый интерес к поиску решения проблемы; мотивация на решение проблемы; устойчивый познавательный интерес.
«Математика - царица наук» и, наверное, не каждый догадывается, что огромный толчок в развитии всей математики дала именно геометрия.
Геометрия – «измеряю землю»
Почти все великие ученые древности и средних веков были выдающимися геометрами. Древнегреческий философ Платон, проводивший беседы со своими учениками в роще «Академа», откуда и пошло название «академия», одним из девизов своей школы провозгласил «Не знающие геометрии не допускаются!»
Было это примерно 2400 лет тому назад. Из геометрии вышла наука, которая называется математикой
Здравствуйте! Тема урока – «Решение треугольников».
Решением треугольника называется нахождение всех его шести элементов (то есть трёх сторон и трёх углов) по каким-нибудь трём данным элементам, определяющим треугольник.
Здесь мы вспомним основные опорные факты и решим в общем виде три типовые задачи на решение треугольников. Вначале напомним важное определение синуса и косинуса для углов α[0º; 180º].
Но, сначала проведём небольшую разминку - определение истинности (ложности) утверждения
1. И В треугольнике против угла в 150º лежит большая сторона.
2. И В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60º.
3. Л Существует треугольник со сторонами 2 см, 7 см, 3 см.
4. И Прямоугольный равнобедренный треугольник имеет равные катеты.
5. Л Сумма длин двух других сторон любого треугольника меньше третьей стороны.
6. И Если острый угол прямоугольного треугольника равен 60º, то прилежащий к нему катет равен половине гипотенузы.
7. Л Существует треугольник с двумя тупыми углами.
8. И В прямоугольном треугольнике сумма острых углов равна 90º.
Молодцы! Продолжаем…
Имеем окружность, радиус 1, верхняя ее часть – оси координат и угол a. Угол a построен следующим образом, положительная полуось х – один луч этого угла. Второй луч высекает точку М на единичной полуокружности. Координаты точки М (хм;ум) назвали: абсцисса хм – это 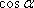 , ордината ум – это
, ордината ум – это 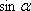 . Итак, имеем ÐАОМ=aÞМ (хм; ум)= М (
. Итак, имеем ÐАОМ=aÞМ (хм; ум)= М (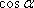 ;
;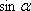 ).
).
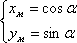
Это для любого угла α[0º; 180º], потому что треугольник имеет любой угол в пределах(0º; 180º). Таким образом, мы просто напомнили определение синуса и косинуса для любого угла, который может быть углом треугольника. Отметим важную специфику: значение косинуса однозначно определяет угол треугольника. Поясним это примерами, объясним почему.
Вот линия косинусов. Косинус может меняться в пределах от -1 до 1.
Пример 1
а) Пусть 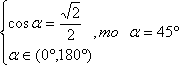 .
.
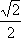 отметил на линии косинусов, перпендикуляр, получил единственную точку М на окружности. И получил нужный угол, этот угол искомый. Почему он равен 45º? Потому что если это
отметил на линии косинусов, перпендикуляр, получил единственную точку М на окружности. И получил нужный угол, этот угол искомый. Почему он равен 45º? Потому что если это 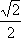 , то и здесь
, то и здесь 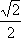 , гипотенуза 1, либо по таблице, либо по этому треугольнику получаем, что имеем угол 45º.
, гипотенуза 1, либо по таблице, либо по этому треугольнику получаем, что имеем угол 45º.
Итак, если при решении задач, мы вдруг увидели 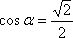 , мы однозначно определяем, что этот угол равен 45º.
, мы однозначно определяем, что этот угол равен 45º.
Второй пример.
б) если 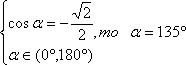 .
.
Вдруг выяснилось, что 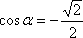 и a – это угол треугольника, то мы должны сразу получить ответ, что a=135º.
и a – это угол треугольника, то мы должны сразу получить ответ, что a=135º.
Почему? Во-первых, можно по таблице, а во-вторых, из чертежа. Единичная полуокружность 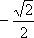 на линии косинусов – это абсцисса точки М, перпендикуляр, получаем точку М. А значит, искомый угол АОМ. Гипотенуза 1, катет в этом треугольнике
на линии косинусов – это абсцисса точки М, перпендикуляр, получаем точку М. А значит, искомый угол АОМ. Гипотенуза 1, катет в этом треугольнике 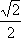 , значит, либо этот угол 45º, а значит, и этот угол 45º. (180º - 45º) = 135º, либо по таблице, раз у нас
, значит, либо этот угол 45º, а значит, и этот угол 45º. (180º - 45º) = 135º, либо по таблице, раз у нас 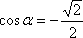 , то угол равен 135º.
, то угол равен 135º.
Итак, специфика заключается в том, что значение косинуса однозначно определяет угол треугольника. В отличие от косинуса значение синуса, если он заключен в пределах
 определяет два угла треугольник a1 и a2 и сумма этих углов равна 180º:
определяет два угла треугольник a1 и a2 и сумма этих углов равна 180º:
a1+a2=180º
Поясним сказанное на чертеже. Единичная полуокружность, оси координат, вот значение синуса. Синус, кстати, меняется от0 до 1, вот синус ≠1, перпендикуляр. Получаем две точки на окружности, точку М и точку N. Только две эти точки имеют свои ординаты, вот это значение, которое равно синусу a. Первая точка определяет один угол АОN – назвали a1. Вторая точка определяет угол АОМ – назвали a2. Но имеем еще один угол a2 в силу симметрии, так что a1+a2=180º. Итак, значение синуса определяет два угла, в сумме составляющих 180º. И это углы треугольника, и это очень важно для решения треугольников.
Сделаем конкретный пример.
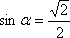 , то a1=135º.
, то a1=135º.
или a2=45º
Если 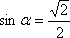 , то мы имеем два конкретных угла. Если это
, то мы имеем два конкретных угла. Если это 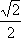 , то один из углов 135º, вот этот большой угол, второй угол45º. Итак, еще раз: значение косинуса однозначно определяет угол треугольника. Значение синуса не однозначно определяет угол треугольника. Значение синуса, если оно не равно 1, определяет два угла треугольника, сумма которых равняется180º.
, то один из углов 135º, вот этот большой угол, второй угол45º. Итак, еще раз: значение косинуса однозначно определяет угол треугольника. Значение синуса не однозначно определяет угол треугольника. Значение синуса, если оно не равно 1, определяет два угла треугольника, сумма которых равняется180º.
Теперь мы знаем, что такое синус и косинус любого, в том числе тупого угла треугольника. Поэтому мы можем определить координаты всех вершин треугольника.
Вот на рисунке остроугольный треугольник и тупоугольный треугольник. Угол g острый, угол g тупой. Во-первых, если мы говорим о координатах, то надо ввести систему координат. Удобно ввести ее следующим образом: начало совместить с одной из вершин, например, с вершиной С. А ось х пустить по прямой СВ. Итак, имеем треугольник АВС. Стандартные обозначения: вершина А, длина стороны – а маленькая; вершина В, длина стороны – в маленькая; вершина С, длина стороны – с маленькая; угол при вершине С=g, стандартное обозначение. Координаты этой точки С – начало координат С(0;0). Координаты этой точки В(а;0), это понятно. И, наконец, координата точки А – это (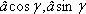 ).
).
Это, во-первых, мы выводили в свое время, а во-вторых, можно это посмотреть из треугольника прямоугольного, в котором ха – катет равен: гипотенуза умножить на косинус прилежащего угла. Противолежащий катет уа есть гипотенуза, умноженная на синус противолежащего угла. Таким образом, вот координаты всех точек: А(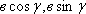 ), В(а;0), С(0;0). По виду они не меняются, если угол g тупой.
), В(а;0), С(0;0). По виду они не меняются, если угол g тупой.
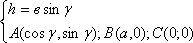
По-прежнему, высота вот из этого треугольника или из этого треугольника h=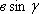 . Формулы для остальных вершин те же самые.
. Формулы для остальных вершин те же самые.
Итак, если мы знаем, что такое синус и косинус для угла треугольника, то мы можем найти координаты всех его вершин через синус и косинус угла. Зная координаты вершин треугольника, мы в свое время получили формулу для площади через синус угла. Напомним ее.
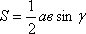
Откуда взялась эта формула? Вспомним, что площадь, мы давно считали по известной формуле:  основания на высоту, которая проведена к этому основанию
основания на высоту, которая проведена к этому основанию 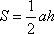 . Но высота есть ордината точки А, а ордината точки А (только что мы говорили) – это
. Но высота есть ордината точки А, а ордината точки А (только что мы говорили) – это 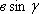 , т.к. h=
, т.к. h=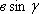 , то подставили в формулу для площади и получили результат:
, то подставили в формулу для площади и получили результат: 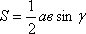 .
.
Итак, площадь треугольника есть половина произведения двух его сторон, длин его сторон, точнее, на синус угла между ними. Далее с помощью этой формулы мы получили теорему синусов. Напомним и ее. Теорема синусов утверждает: отношение длины стороны к синусу противолежащего угла треугольника есть величина постоянная для данного треугольника, а именно:
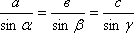 .
.
Напомним также, что вывод мгновенно следует из формулы из площади треугольника
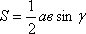 =
=
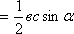 =
=
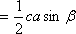
Важным инструментом при решении треугольников является теорема косинусов. Напомним ее. Вот ∆АВС, сторона а, сторонаb, сторона с. Треугольник помещен в координатную плоскость, оси координат х, у. Координаты каждой вершины мы сейчас умеем находить. Вот координаты вершины А(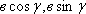 ), это
), это 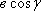 – одна координата, абсцисса;
– одна координата, абсцисса; 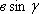 - вторая координата, ордината. Через эти координаты мы находим длину АВ, и в результате получили теорему косинусов, которая звучит следующим образом: с2=а2+в2-2ав
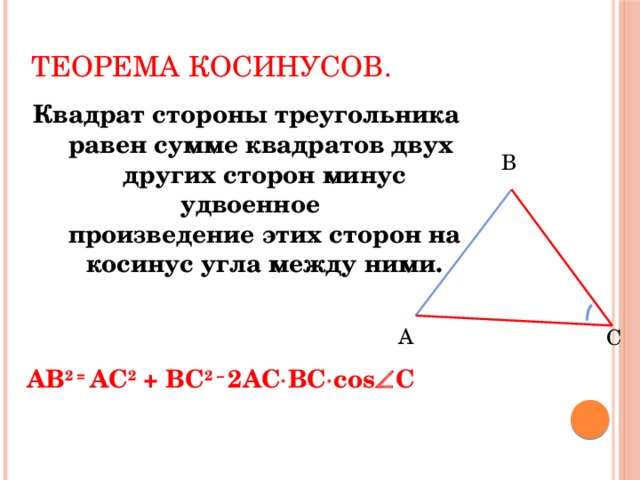
- вторая координата, ордината. Через эти координаты мы находим длину АВ, и в результате получили теорему косинусов, которая звучит следующим образом: с2=а2+в2-2ав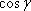 . Напомним словесную формулировку: квадрат стороны равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
. Напомним словесную формулировку: квадрат стороны равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Это, как мы помним, обобщение теоремы Пифагора. Если бы угол g был прямым, то с была бы гипотенузой, квадрат гипотенузы был бы равен сумме квадратов катетов. Но это для прямоугольного треугольника. Теорема косинусов для любого треугольника. И теорема синусов, и теорема косинусов – это важнейшие инструменты для решения треугольников. Напомним, что означает слово «решение треугольников». Это означает, что следует найти все стороны, все три стороны и все три угла треугольника. Вот одна из типовых задач.
Задача
В ∆АВС даны а, в, g (две стороны и угол между ними). Даны три элемента треугольника. Найти с, a, b, т.е. остальные элементы треугольника. Прокомментируем еще раз условия. Вот ∆АВС, сторона а, длина ее известна. Сторона в, длина ее известна. И величина угла между ними, т.е. три элемента треугольника известны. Надо найти остальные три элемента, т.е. должны быть известны три стороны, длины этих сторон и величины углов.
Решение:
1) с=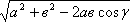
2) 
3) b=180º-(a+g).
Вот известен угол g, всегда полезно написать теорему косинусов для противоположной стороны.
1) Написали с2=а2+в2-2ав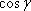 .
.
Для того чтобы найти с, надо взять Ö из этого выражения. Таким образом, теорема косинусов мгновенно позволяет найти противолежащую сторону, противолежащую углу g. Нашли. Значит, каким образом найти угол a?
2) Для этого надо написать теорему косинусов для противоположной стороны:
 , т.е. написали теорему косинусов для противоположной стороны, получили уравнение для косинуса и нашли косинус. Нашли косинус, а по косинусу угла находим сам угол, причем мы говорили, что угол a в треугольнике однозначно задан, если задан косинус этого угла. Итак, угол a найден.
, т.е. написали теорему косинусов для противоположной стороны, получили уравнение для косинуса и нашли косинус. Нашли косинус, а по косинусу угла находим сам угол, причем мы говорили, что угол a в треугольнике однозначно задан, если задан косинус этого угла. Итак, угол a найден.
3) Осталось найти угол b. Сумма трех углов треугольника 180º, значит, угол b – это 180º минус сумма двух уже известных нам углов a и g.
Таким образом, первая стандартная задача решена. Напомним ее связь с признаком равенства треугольников. Ведь два треугольника равны, если две стороны соответствующие равны и угол между ними равен. То есть две стороны и угол однозначно задают треугольник. Вот они заданы, и получился треугольник. Все остальные элементы этого треугольника мы нашли с помощью теоремы косинусов. Задача решена.
Следующая типовая задача по решению треугольников.
Задача. В ∆АВС известна длина стороны а, величины углов b и g (сторона и два прилежащих к ней угла). Требуется решить треугольник, т.е. найти недостающие элементы, а именно: величину угла a, в, с – длины сторон. Решение. Используем теорему синусов, нам нужно найти длину в:
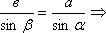
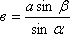 .
.
Длина одной стороны найдена по теореме синусов. Далее находим длину третьей стороны по той же теореме синусов: 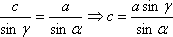 . Задача решена.
. Задача решена.
Треугольник, как мы знаем, задается тремя сторонами. Следующая задача опирается на этот факт.
Задача. В ∆АВС даны длины трех сторон а, в, с. Найти все углы a, b, g. Стандартные обозначения, треугольник поясняет сказанное. Стороны известны, надо найти углы. Решение: по теореме косинусов пишем теорему косинусов для стороны а и находим косинус угла a
1) 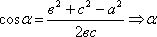
Такова теорема косинусов для угла a для стороны а. Нашли косинус, а по косинусу мы однозначно находим угол a. Аналогично действуем для косинуса b.
2) 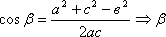
Нашли косинус b, он однозначно задает угол b. Если мы знаем два угла треугольника a и b, то третий угол находим как разность:
3) g=180º-(a+b)
Задача решена.
Итак, мы повторили основные опорные факты и решили три типовые задачи по решению треугольников. На следующем уроке мы продолжим решение треугольников в основном с конкретными исходными данными.
Домашнее задание: № 1020-1022 стр. 261
Спасибо за урок!







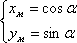
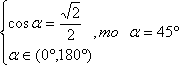 .
.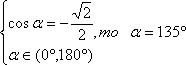 .
.












 а 2 +в 2 остроугольный , если с 2 прямоугольный , если с 2 = а 2 +в 2" width="640"
а 2 +в 2 остроугольный , если с 2 прямоугольный , если с 2 = а 2 +в 2" width="640"





























