Решение задач методом ключевых ситуаций

Обучение решению задач методом ключевых ситуаций

Преподаватель физики ГБПОУ «КМТ»

З. Г. Хасанова (по материалам вэбинаров

Организованных издательством БИНОМ)

Метод ключевых ситуаций – обучение решению задач методом постановки задач

Типовое задание: ИССЛЕДОВАТЬ предложенную ситуацию:

• определить, какие закономерности для неё справедливы;
• применить их для постановки задач и их решения;
• изменить ситуацию и исследовать последствия изменений.

Важно научить студентов видеть в формулах не шаблоны для подстановки численных значений при решении уже поставленных задач, а источник задач .

Задачи — это не контроль «усвоения теории», а способ освоения теории .

Возможность организовать работу всей группы (учимся, играя).

• Необходима система обучающих задач, которые учат исследованию.
• Это – задачи на постановку вопросов!
• Если в курсе физики изучают так мало явлений, то откуда берутся тысячи задач?
• Если наши студенты найдут ответ на этот вопрос, они получат «золотой ключик», потому что научаться ставить задачи.

Методика использования МКС

• По описанию ключевой ситуации вместе со студентами ставим вопросы , применительно к этой ситуации.
• Рассматриваем как ответы на эти вопросы порождают новые вопросы – а это уже исследование.
• Формируем у студентов исследовательский подход: они не только решают задачи , но сами их ставят.

РАСЧЁТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

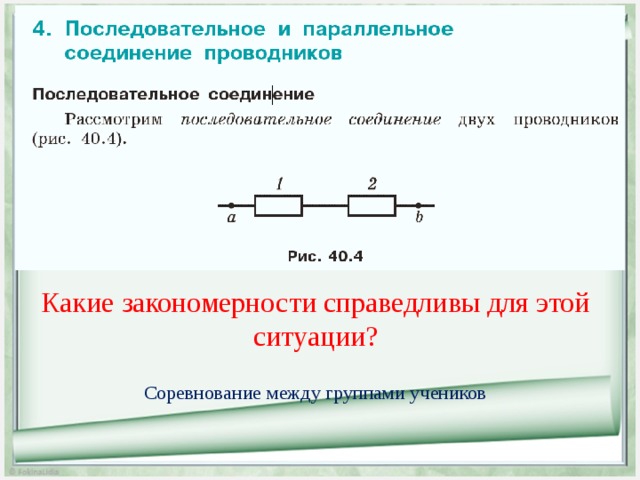
Какие закономерности справедливы для этой ситуации?

Соревнование между группами учеников

Воспользуйтесь законом сохранения электрического заряда и определением силы тока.

Воспользуйтесь тем, что работа электростатического поля по перемещению заряда по двум последовательно соединённым проводникам равна сумме работ по перемещению заряда по каждому проводнику.

Разделите уравнение U = U 1 + U 2 на силу тока I в данном участке цепи и воспользуйтесь тем, что I = I 1 = I 2 .

Чему равны общее сопротивление, сила тока,

напряжения на проводниках?

«Теория» усваивается в задачах!

Какие наборы физических величин ПОЛНОСТЬЮ определяют ситуацию?

Соревнование между группами учеников

Какие задачи можно поставить, используя эти соотношения?

Соревнование между группами учеников

Генератор задач по ключевой ситуации

• Взять любой набор физических величин, полностью определяющих ситуацию.
• Задать значения этих величин и найти значения всех остальных величин, используя написанные соотношения.
• Для составления задач можно выбирать из полученного набора значений всех величин некоторые в качестве заданных . Цель: найти значения остальных величин ( искомых ).

• Можно эффективно использовать при составлении вариантов заданий для самостоятельных и контрольных работ.

Пример

А

А

Б

Качественное исследование ключевой ситуации

• Качественное исследование самое полезное для формирования физической интуиции , а обучение физике — это прежде всего формирование физической интуиции (а не заучивание формулировок законов и определений!).
• Качественные задания — одни из наиболее трудных на экзаменах, потому что требуют понимания физических процессов и явлений , а не подстановки численных значений в готовые формулы.
• Для успешного решения качественных задач и качественного исследования ситуации нужно научить ребят видеть в физической формуле не шаблон для подстановки численных значений, а вид функциональной зависимости : от чего и как зависит величина, выражаемая формулой, и как она изменяется (уменьшается или увеличивается) при изменении входящих в формулу величин.

Наибольшее напряжение на резисторе 4 , наименьшее — на резисторах 1 и 2.

Наибольшая сила тока в резисторе 4 , наименьшая — в резисторах 1 и 2 .

Наибольшая мощность тока в резисторе 4 , наименьшая — в резисторах 1 и 2 .

Р 2 станет равной нулю, Р 3 увеличится, Р 4 не изменится.

Р 2 увеличится, Р 3 уменьшится, Р 4 не изменится.