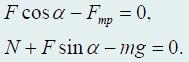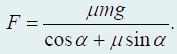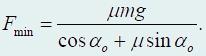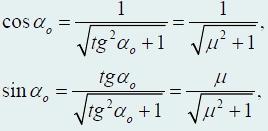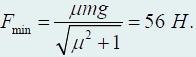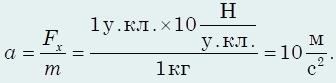Практикум по решению задач на тему

Опубликовано 26.09.2016 - 20:51 - Воронина Ирина Геннадьевна
1. После спуска с сортировочной горки железнодорожная платформа массой 9000 кг имела скорость 2 м/с и двигалась до полной остановки в течение 10с. Какова равнодействующая всех сил, действовавших на платформу?
Решение: 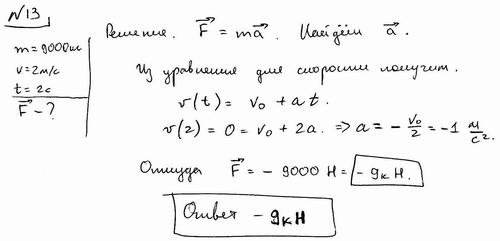
2. Лыжник массой 80 кг в конце спуска с горы приобрёл скорость 12 м /с и продолжал двигаться по горизонтальной поверхности. Через сколько времени он остановится, если сила трения, действующая на него, равна 16 Н ?
Решение: 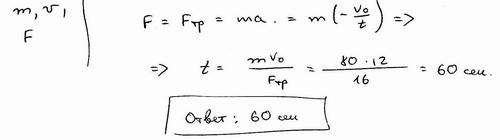
3. Брусок массой m тянут по полу с постоянной скоростью, действуя на него силой F, направленной под углом α к направлению движения. Ускорение свободного падения g. Чему равна вертикальная составляющая силы Fy с которой пол действует на брусок?
 Решение:
Решение: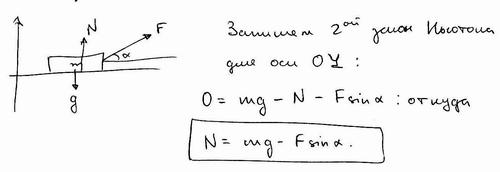 Ответ:
Ответ:
4. Тело поднимают вверх по наклонной плоскости, прикладывая к нему горизонтальную силу, величина которой вдвое больше действующей на тело силы тяжести. Высота наклонной плоскости 3 м, её длина 5 м. Найдите ускорение тела, если коэффициент трения равен 0,2
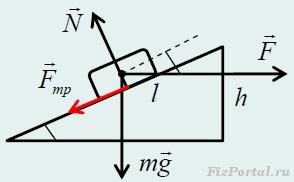
Запишем второй закон Ньютона в проекции на направление плоскости в направлении действия силы F.
ma = Fcosα − mgsinα − Fmp,
где
Fmp = μN = μmgcosα + Fsinα.
Тогда
ma = Fcosα − mgsinα − μ(mgcosα + Fsinα). (1)
Учтем, что по условию задачи F = 2mg, а sinα = h/l, а cosα = √(l2 − h2)/l, подставляя в уравнение (1) и сокращая на массу, получим
a = 2g√(l2 − h2)/l − gh/l − μ(g√(l2 − h2)/l + 2gh/l).
Рассчитаем ускорение
a = 2•10•√(52 − 32)/5 − 10•3/5 − 0,2•(10•√(52 − 32)/5 + 2•10•3/5) = 6 м/с2.
Ответ: a = 6 м/с2.
Замечания: при решении задач такого типа, возможно проще будет, если мы рассчитаем отдельно sinα = 3/5 = 0,6 и cosα = √(52 − 32)/5 = 0,8. Тогда уравнение второго закона будет проще
ma = 0,8F − 0,6mg − μ(0,8mg + 0,6F)
или
a = 16 − 6 − 0,2(8 + 12) = 6 м/с2.
5. Вверх по наклонной плоскости высотой 9 м и длиной 15 м пущена шайба. Коэффициент трения равен 0,5. Найдите ускорение шайбы. В ответе укажите абсолютную величину ускорения.
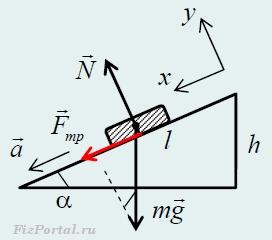
На рисунке шайба движется вверх по наклонной плоскости. Ускорение шайбе сообщают приложенные к ней силы: сила тяжести и сила взаимодействия шайбы с плоскостью, которую для удобства разложим на две составляющие: силу трения и реакцию опоры. Запишем уравнение второго закона Ньютона в проекции на оси x и y:
ma = mgsinα + Fmp и 0 = N – mgcosα
С учетом того, что сила трения скольжения равна
Fmp = μN = μmgcosα,
получим
a = gsinα + μgcosα.
Где sinα = h/l = 0,6, а cosα = √(1 – (h/l) 2) = 0,8.
Вычислим
a = 10•0,6 + 0,5•10•0,8 = 10 м/с2.
Ответ: a = 10 м/с2.
6.По наклонной плоскости скользит с ускорением a = 1 м/с2 брусок массой m = 200 г. С какой силой F нужно прижимать брусок перпендикулярно наклонной плоскости, чтобы он начал двигаться равномерно? Коэффициент трения бруска о наклонную плоскость μ = 0,1.
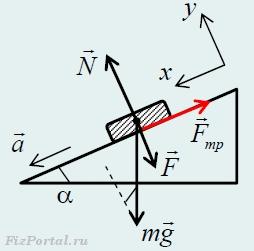
Запишем уравнение второго закона Ньютона в проекции на направление осей x и y при движении с ускорением a:
ma = mgsinα − Fmp и 0 = N − mgcosα.
С учетом того, что сила трения скольжения равна
Fmp = μN = μmgcosα,
получим
ma = mgsinα − μmgcosα. (1)
При равномерном движении, силы вдоль направления движения по наклонной плоскости, компенсируют друг друга
mgsinα = Fmp = μ(mgcosα + F);. (2)
Сделаем замену (2) в (1)
ma = μ(mgcosα + F) − μmgcosα.
Откуда ma = μF и F = maμ.
Вычислим F = 0,2•1•0,1 = 2 Н.
Ответ: F = 2 Н.
7.На столе лежит деревянный брусок массой М = 2 кг, к которому привязана нить, перекинутая через блок, укрепленный на краю стола. К свободному концу нити подвешен груз массой m = 1 кг, вследствие чего брусок движется с ускорением а = 0,6 м/с2. Каковы будут ускорения груза и бруска, а также натяжение нити, если вся система будет: а) подниматься с ускорением а = 2,2 м/с2; б) опускаться с тем же по модулю ускорением?
Решение.
Запишем уравнение второго закона Ньютона
mg − μMg = (m + M)a. (1)
а) Если переносное ускорение системы a1, относительное ao, то уравнение второго закона Ньютона для груза имеет вид:
T − mg = m(a1 − ao), (2)
для бруска:
T − μN = Mao, (3)
и
N − Mg = Ma1. (4)
Модуль полного ускорения груза
aг = a1 − ao, (5)
бруска
aб = √{ao2 + a12}. (6)
Из уравнений (1) − (6) находим:
aг ≈ 1,46 м/с2; aб ≈ 2,3 м/с2; Т = 11,2 H.
б) aг ≈ 2,66 м/с2; aб ≈ 2,24 м/с2; Т ≈ 7 H.
8. С помощью прочного троса груз равноускоренно поднимают с поверхности земли вертикально вверх. Через Δt = 5,0 с после начала подъема груз уже находился на высоте h = 15 м, продолжая движение. Сила тяги подъемного механизма к этому моменту времени, когда тело достигло высоты h = 15 м, совершила работу А = 8,4 кДж. Определите массу поднимаемого груза.
Решение.
На груз действует сила тяги и сила тяжести.
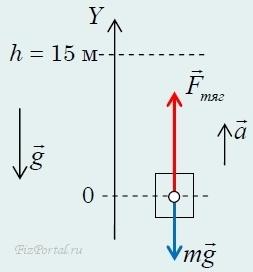
По второму закону Ньютона
ma = Fтяг + mg. (векторно)
В проекции на вертикальную ось
ma = Fтяг − mg.
Откуда сила тяги
Fтяг = ma + mg.
Работа силы тяги
A = Fтягh = m(a + g)h. (1)
Из кинематики определим ускорение
h = aΔt2/2, a = 2h/Δt2. (2)
Из (1) выражаем искомую массу груза и подставляем ускорение из (2)
m = A/((2h/Δt2 + g)h).
Подставим численные значения
m = 8400/((2•15/52 + 10) × 15) = 50 (кг).
Ответ: масса поднимаемого груза 50 кг.
9. Брусок массой m = 2,0 кг движется без начальной скорости по горизонтальной поверхности под действием силы, модуль которой F = 10 Н, направленной параллельно этой поверхности. Коэффициент трения между бруском и поверхностью μ = 0,20. Через какой промежуток времени Δt, модуль скорости у тела станет равным v = 30 м/с.
Решение:
По второму закону Ньютона, ускорение получаемое телом есть результат приложенных к нему сил (равнодействующей силы).
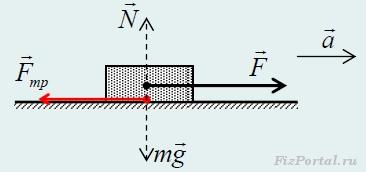
Результирующая сила равна разности приложенной силы F и силы трения. Сила тяжести и реакция опоры направлены перпендикулярно к направлению движения тела.
a = (F − Fmp)/m = (F − μmg)/m. (1)
Воспользуемся уравнением скорости v = vo + at, при vo = 0, v = at. Искомое время t = v/a. После подстановки (1) получим
t = mv/( F – μmg).
После подстановки численных значений, имеем
t = 2•30/(10 − 0,2•2,0•10) = 10 (c).
Ответ: t = 10 c.
10. С какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать сани массой m = 10 кг по горизонтальному асфальту, если коэффициент трения скольжения μ = 0,7?
Решение.
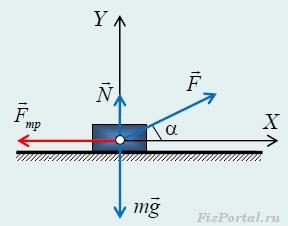
Запишем уравнения движения санок в проекциях на горизонтальное и вертикальное направления:
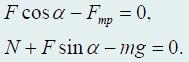
где α − угол между веревкой и горизонтом, а сила трения Fmp = μN.
Из написанной выше системы уравнений найдем силу натяжения веревки
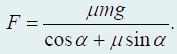
Теперь проанализируем зависимость силы F от угла α. Санки будут двигаться равномерно, если горизонтальная составляющая силы реакции веревки Fcosα равна силе трения Fmp. Для обеспечения минимальности силы F веревку, казалось бы, надо тянуть горизонтально, так как в этом случае sinα = sin0° = 0. C другой стороны, желательно, чтобы угол α был побольше, так как в этом случае за счет увеличения вертикальной составляющей Fsinα, стремящейся приподнять санки, уменьшается их давление на опору и, соответственно, уменьшается сила трения. Таким образом, на результат влияют два конкурирующих фактора.
Представим зависимость F(α) в виде графика.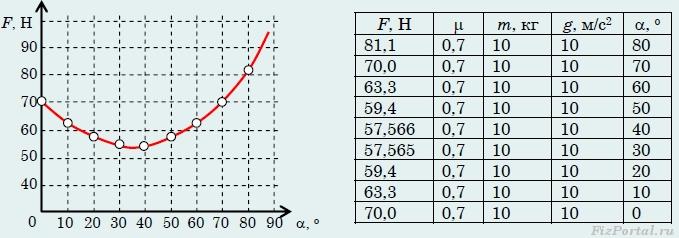
Из графика видно, что исследуемая функция имеет минимум. Для нахождения значений αmin и Fmin воспользуемся аналитическим методом. Функция F(α) минимальна, если знаменатель максимален. Обозначим его буквой y, найдем производную y по α и приравняем ее к нулю:
y/ = −sinα + μcosα = 0.
Отсюда, обозначив соответствующий угол αo, получим
tgαo = μ; αo = 35°.
Тогда
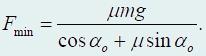
Используя соотношения
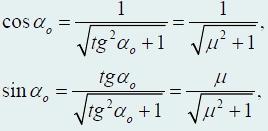
найдем искомую величину
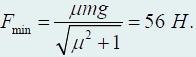
11.На рисунке изображены три силы, которые подействовали на тело массой 1 кг, покоящееся в инерциальной системе отсчета. Если одна клеточка соответствует силе 10 Н, то тело тело будет двигаться … с модулем ускорением …
1) по направлению силы F2, 10 м/с2; 2) по направлению силы F3, 5 м/с2;
3) по направлению силы F1, 10 м/с2; 4) против направления силы F2, 10 м/с2;
5) тело будет покоится, 0 м/с2.
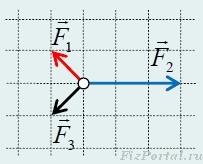
Решение.
Разложим вектора сил на направления осей x и y. Обратим внимание на то, что вдоль оси х, результирующая сил равна
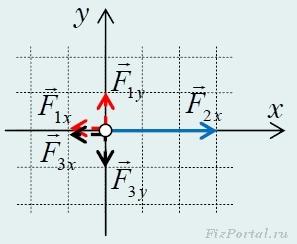
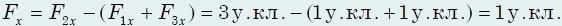
Вдоль оси y результирующая сил равна
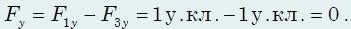
В результате действия трех сил тело будет двигаться по направлению оси x, т.е. по направлению силы F2, с ускорением равным
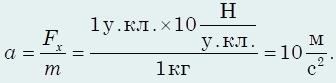
Выбираем правильным ответ 1) по направлению силы F2, 10 м/с2.








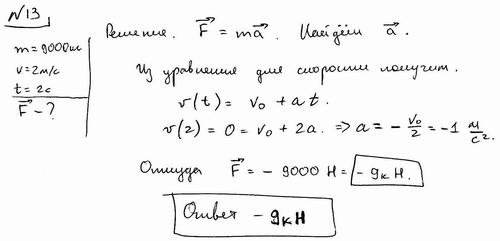

 Решение:
Решение: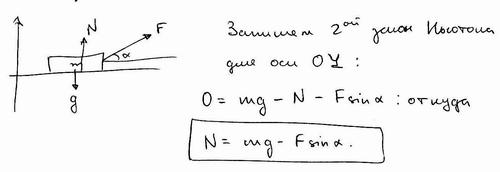 Ответ:
Ответ: