Тема урока: Решение задач по теме: «Площадь»
Цели урока:
Формировать умения решать задачи на применение формул площади треугольника, трапеции, параллелограмма, других фигур.
Прогнозируемый результат:
Знать основные свойства фигур, формулы площадей параллелограмма, треугольника, трапеции.
Уметь применять свойства фигур, формулы площадей фигур при решении задач практического содержания.
Оборудование:
индивидуальный раздаточный материал.
Ход урока.
1.Сообщение темы и цели урока.
Здравствуйте, ребята.
Сегодня мы с вами повторим формулы площадей различных фигур и некоторые задания на применение формул.
Цель нашего урока: обобщить теоретические знания и сформировать практические навыки применения формул в различных У вас на столах индивидуальные задания с готовыми чертежами, по ходу урока я скажу как их использовать.
2. Каждый ученик вытаскивает геометрическую фигуру и перечисляет основные свойства фигур, формулы площадей фигур.
3. Сопоставить геометрической фигуре формулу площади
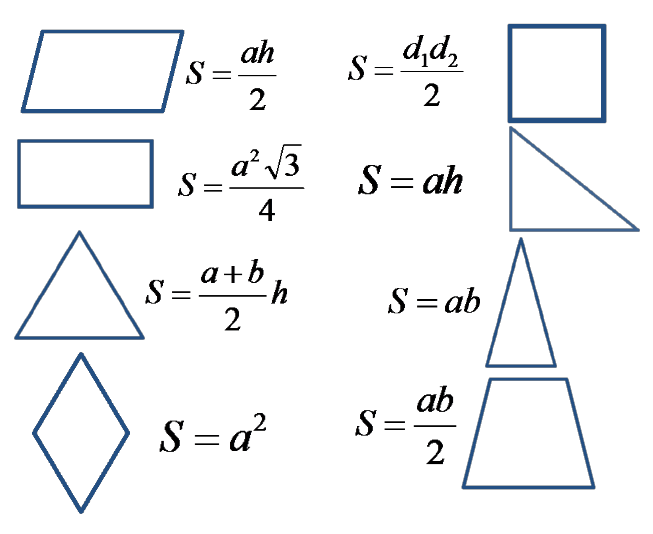
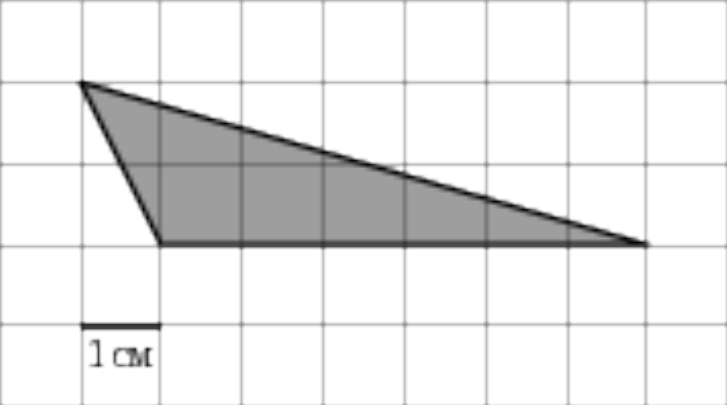
4.Устная работа с чертежами на клетчатой основе. Теперь применим эти формулы для вычисления площадей фигур, я вам уже говорила, что такие задания включены в экзаменационную работу и в ГИА и в ЕГЭ.
В каждом задании надо найти площадь закрашенной фигуры, размер клетки 1см*1см, на столах у вас такие задания.
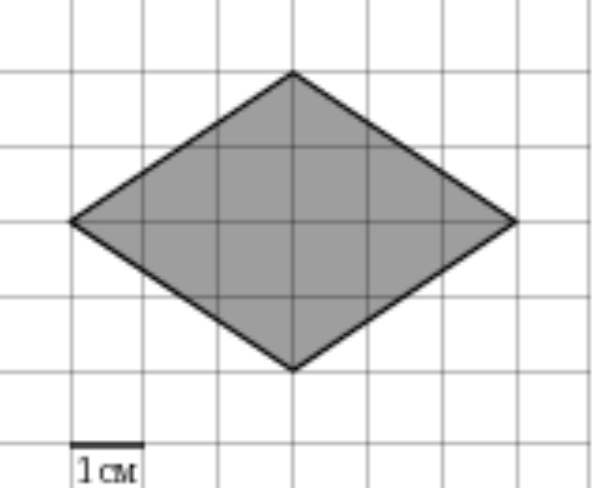
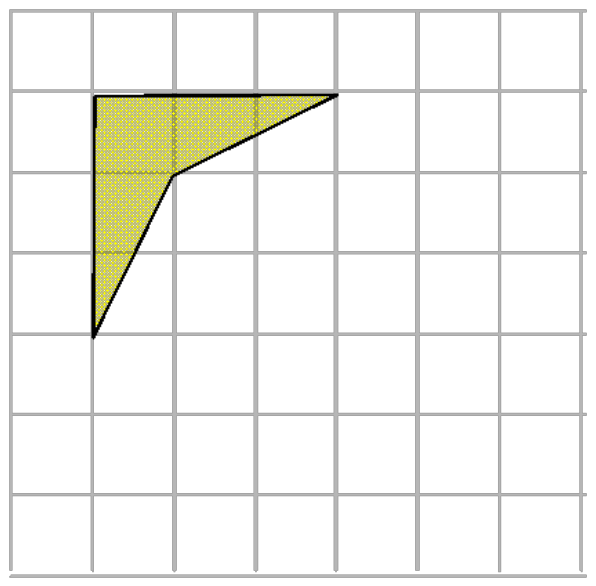
5 Выберете верное утверждение:
| 1) Площадь прямоугольного треугольника равна произведению его катетов. 2) Площадь прямоугольника равна произведению двух его сторон. 3) Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне. 4) Площадь трапеции равна полусумме ее оснований |
| 5) Площадь ромба равна половине произведения его стороны и высоты, проведённой к этой стороне. 6) Площадь параллелограмма равна произведению двух его сторон 7) Площадь треугольника равна произведению его основания на высоту |
| 8) Площадь прямоугольника равна его периметру. 9) Площадь ромба равна половине произведения его диагоналей |
| 10) Площадь квадрата равна квадрату его диагонали. 11) Площадь параллелограмма равна половине произведения его основания на высоту. |
|
12) Площадь параллелограмма равна половине произведения его стороны на высоту, проведённую к этой стороне 13) Площадь ромба равна половине произведения его сторон. |
| 14) Если площади фигур равны, то равны и сами фигуры. 15) Если диагонали ромба равна 3 и 4, то его площадь равна 6. 16) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. |
| 17) Площадь прямоугольника равна произведению его смежных сторон 18) Площадь трапеции равна произведению полусумме ее оснований на высоту.
|
6. В следующих задачах вам надо найти площадь фигуры на готовом чертеже и выбрать ответ (5 мин.).
| 1. | 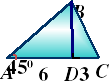
|
| 2. | 
|
| 3. | 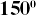
|
| 4. | 
|
| 5. |  BD=14см, АС=48 см BD=14см, АС=48 см
Найти площадь ромба ABCD. |
7. Подведение итогов. Проверка ответов по таблице (слайд с таблицей) Ребята, те, кто закончил работу над задачами, могут проверить себя, перед вами таблица ответов.
8.Запишите домашнее задание №458, №481 , стр.133 вопросы с 1 по 10
9.Итог урока, оценки за урок. Релаксия.(1 мин.)
Наш урок заканчивается, надеюсь, он был вам полезен, в дальнейшем мы узнаем на сколько ещё широк спектр формул площадей фигур.
А теперь задайте себе вопрос: научился ли я применять формулы площади?













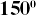

 BD=14см, АС=48 см
BD=14см, АС=48 см




















