
ПРОЕКТ ПО МАТЕМАТИКЕ ТЕМА: «РИСУНОК В КООРДИНАТНОЙ ПЛОСКОСТИ» Выполнил: Виноградов Савелий 6 «Б» класс МОУ гимназии им. А.Л. Кекина

ПЛАН ПРОЕКТА
1
История возникновения системы координат
Задачи, решаемые в системе координат
2
Рисунок в координатной плоскости
3
3
Список использованных источников и литературы
4
4

ЦЕЛЬ ПРОЕКТА 1. Изучить историю возникновения системы координат 2. Научиться строить систему координат и определять координаты точки на плоскости 3. Узнать какие задачи решаются в системе координат 4. Нарисовать рисунок в координатной плоскости

История системы координат
ГИППАРХ ПТОЛЕМЕЙ РЕНЕ ДЕКАРТ

Более чем 100 лет до н.э. греческий учёный Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо известные теперь географические координаты: широту и долготу и обозначить их числами.

Во II веке н.э. знаменитый древнегреческий астроном Клавдий Птолемей уже пользовался широтой и долготой в качестве географических координат.

Гениальный французский учёный и мыслитель XVII в. Рене Декарт хотел создать такой универсальный математический метод, который позволил бы всякому овладевшему им решить задачу. Главное достижение Декарта – построение аналитической геометрии. Он перевёл на алгебраический язык задачи на построение циркулем и линейкой. Декартова система координат сильно повлияла на развитие математики. Алгебраическое уравнение Декарт рассматривал как зависимость между X и Y, определяемую положение точек на плоскости.

Задачи, решаемые в системе координат
Для того, чтобы определить координаты точки на плоскости, проведём в этой плоскости две взаимно перпендикулярные числовые оси – это и будет система координат. Точку их пересечения берут за начало отсчёта осей Ox и Oy и называют началом координат О.
Направление осей выбирают так, чтобы положительная полуось Ох при повороте на + 90 градусов совмещалась с положительной полуосью Оу. Единичные отрезки на осях чаще выбирают одинаковыми и наносят шкалы. Ох-ось абсцисс, Оу-ось координат
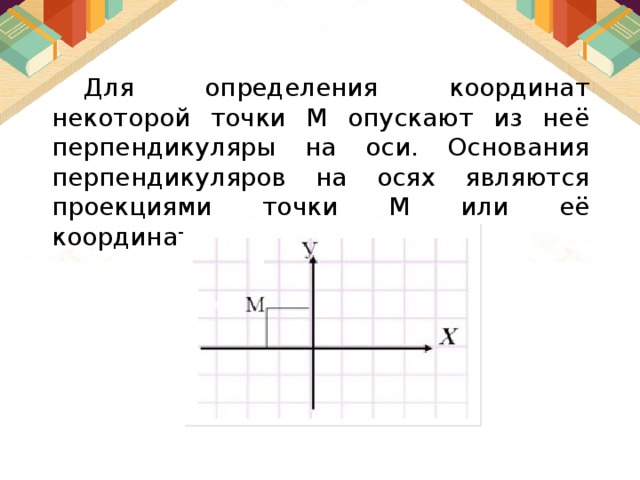
Для определения координат некоторой точки М опускают из неё перпендикуляры на оси. Основания перпендикуляров на осях являются проекциями точки М или её координатами.

Итак, в системе координат решаются две задачи:
- Построение точек на плоскости по заданным координатам.
Заданы координаты точек:
В (1,0)
К (3,4)
Р (-2,1)
С (0,-3)

2. Нахождение координат точек, расположенных на плоскости. На плоскости заданы точки : Е, Т, С, Р, Н
Кроме того, что на плоскости можно изобразить рисунок, заданный координатами, также можно на координатной плоскости решать уравнения и изображать рисунки, которые заданы отрезками функций: линейной, квадратичной, обратной пропорциональности, кубической

Рисунок в координатной плоскости
(-25;-3); (-25;0); (-23;2); (-23;12); (-25;14); (-25;16); (-22;18); (18; 9); (9;25); (9;28); (12; 30); (18;30); (21; 28); (21; 18); (25;16); (25; 14)
1 Арка: (-25; -3); (-25;0); (-23;2); (-23;12); (-25;14); (-19;14); (-21;12); (-21;1); (-20;0); (-20;-3); (-25;-3)
2 Арка : (-10;-3); (-10;0); (-8;1); (-8;12); (-10;14); (-4;14); (-6;12); (-6; 1); (-4;0); (-4;-3); (-10;-3)
3 Арка : (5;-3); (5;0); (6;1); (6;12); (4;14); (10;14); (8;12); (8;1); (10;0); (10;-3); (4;-3)
4 Арка: (19;-3); (19;0); (21;1); (21;12); (19;14); (25;14); (23;12); (23;1); (25;0); (25;-3); (19;-3)
1окно: (-17;2); (-17;8); (-15;10); (-14;10); (-12;8); (-12;2); (-17;2)
2окно: (-2;2); (-2;8); (0;10); (1;10); (2;8); (2;2); (-2;2)
3окно: (12;2); (12;8); (14;10); (15;10); (17;8); (17;2);(12;2)
4окно: (13;20); (13;24); (17;24); (17;20); (13;20)
Соединить точки : (23;1) и (-21;1); (-23;12) и (-21;12); (-8;1) и (-6;1); (6;1)и (8;1); (6;12) и (8;12); (21;1) и (23;1); (21;12) и (23;12) , (-25;14) и (25;14); ( -22;18) и (-22;14); (-15;18) и (-15; 1); (0;18) и (0; 14); (9;18) и (9;14); (15; 17) и (15;14); (21;18) и (21; 14);(9;25) и (11; 26); (11;26) и (19; 26); (21;25) и (19; 26); (13;30) и (12;26); (15;30) и ( 15;26); (17;30) и (18;26); (13;20) и (17;24); (13; 24) и (15; 10); (-16;9)и (-16;2); (-13;9) и (-13;2); (17;7) и (12;7); (-17;4) и (-12;4); (-2; 7)и (2;7); (-2;4) и (2;4); (-1;9) и (-1;2); (14;9) и (14;2); (17;9) и (17; 2); (12;7) и (17;7); (12;4) и (17;4); (9;18) и (11; 17); (11; 17) и (19;17); (19;17) и (21;18); (11;26) и (11;17); (19;26) и (19;17);(-6;1) и (6;1); (-6;0) и (6;0); (-4;1) и (-4;0); (-1;1) и (-1;0); (1;1) и (1;0); (4;1) и (4;0)

МОЙ РИСУНОК

Список используемых источников и литературы
1.Понамарёва Т.Д. «Я познаю мир»,АСТ, 2004 г.
2. Источники сети интернет
СПАСИБО ЗА ВНИМАНИЕ!































