МБОУ «Открытая (сменная) школа №2» города Смоленска
Самостоятельные и контрольные работы
по теме: «Многочлены»
7 класс
Выполнила
учитель математики
Мищенкова Татьяна Владимировна.
Cамостоятельная работа
(проводится с целью закрепления и применения знаний и умений умножения одночлена на многочлен)
Вариант 1
1. Выполните умножение:
a) 3b2 (b –3);
б) 5x (x4 +x2 – 1).
2. Упростите выражения:
a) 4 (x+1) +(x+1);
б) 3a (a – 2) – 5a(a+3).
3. Решите уравнение:
20 +4(2x–5) =14x +12.
4. Дополнительное задание.
Какой одночлен нужно вписать вместо знака *, чтобы выполнялось равенство:
(m+n) * * = mk + nk.
Вариант 2
1. Выполните умножение:
a) - 4x2 (x2 –5);
б) -5a (a2 - 3a – 4).
2. Упростите выражения:
a) (a–2) – 2(a–2);
б) 3x (8y +1) – 8x(3y–5).
3. Решите уравнение:
3(7x–1) – 2 =15x –1.
4. Дополнительное задание.
Какой одночлен нужно вписать вместо знака *, чтобы выполнялось равенство:
(b+c – m) * * = ab + ac – am.
Вариант 3
1. Выполните умножение:
a) – 7x3 (x5 +3);
б) 2m4 (m5 - m3 – 1).
2. Упростите выражения:
a) (x–3) – 3(x–3);
б) 3c (c +d) + 3d(c–d).
3. Решите уравнение:
9x – 6(x – 1) =5(x +2).
4. Дополнительное задание.
Какой одночлен нужно вписать вместо знака *, чтобы выполнялось равенство:
* * (x2 – xy) = x2y2 – xy3.
Вариант 4
1. Выполните умножение:
a) – 5x4 (2x – x3);
б) x2 (x5 – x3 + 2x);
2. Упростите выражения:
a) 2x(x+1) – 4x(2–x);
б) 5b (3a – b) – 3a(5b+a).
3. Решите уравнение:
-8(11 – 2x) +40 =3(5x - 4).
4. Дополнительное задание.
Какой одночлен нужно вписать вместо знака *, чтобы выполнялось равенство:
(x – 1) * * = x2y2 – xy2.
Cамостоятельная работа
(проводится с целью формирования умений и навыков решения уравнений и задач)
Вариант 1
1. Используя образец решения, выполните задание.
| Образец решения | Задание |
| Решите уравнение: 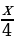 + + 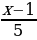 = 6 = 6
Решение: (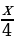 + + 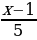 ) * 20 = 6*20, ) * 20 = 6*20,
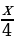 * 20 – * 20 – 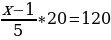 , ,
5x – 4(x – 1) =120, 5x – 4x + 4=120, x=120 – 4, x=116. Ответ: 116.
| Решите уравнение: 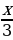 + + 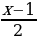 = 4 = 4
|
2. Решите задачу:
На путь от поселка до станции автомобиль потратил на 1 час меньше, чем велосипедист. Найдите расстояние от поселка до станции, если автомобиль проехал его со средней скоростью 60 км/ч. А велосипедист 20 км/ч.
Вариант 2
1. Используя образец решения, выполните задание.
| Образец решения | Задание |
| Решите уравнение: 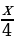 – – 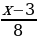 = 1 = 1
Решение: (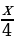 + + 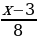 ) * 8 = 1*8, ) * 8 = 1*8,
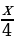 * 8 – * 8 – 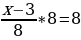 , ,
2x - (x – 3) =8, 2x – 4x + 3=8, x = 8 – 3, x=5. Ответ: 5.
| Решите уравнение: 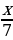 + + 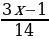 = 2 = 2
|
2. Решите задачу:
Мастер изготавливает на 8 деталей в час больше, чем ученик. Ученик работал 6 часов, а мастер 8 часов, и вместе они изготовили 232 детали. Сколько деталей в час изготовил ученик?
Указания к решению:
а) заполните таблицу;
| Участники | Время работы | Количество деталей в час | Всего изготовили |
| Ученик |
| 
|
|
| Мастер |
|
На 8 деталей больше |
|
б) составьте уравнение;
в) решите уравнение;
г) сделайте проверку и запишите ответ.
Вариант 3
(Для сильных учащихся, дан без образца)
1. Решите уравнение:
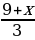 –
– 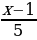 = 2
= 2
2. Решите задачу:
В столовую привезли картофель, упакованный в пакеты по 3 кг. Если бы он был упакован в пакеты по 5 кг, то понадобилось бы на 8 пакетов меньше. Сколько килограммов картофеля привезли в столовую?
Самостоятельная работа проводится в конце урока. После выполнения работы используется самопроверка по ключу.
Самостоятельная работа
(проводится с целью формирования умений и навыков вынесения общего множителя за скобки)
Вариант 1
1. Вынесите общий множитель за скобки (проверьте свои действия умножением):
а) mx + my; д) x5 – x4;
б) 5ab – 5b; е) 4x3 – 8x2;
в) – 4mn + n; * ж) 2c3 + 4c2 + c;
г) 7ab – 14a2; * з) ax2 + a2.
2. Дополнительное задание.
Докажите, что значение выражения 82 – 218 делится на 14.
Вариант 2
1. Вынесите общий множитель за скобки (проверьте свои действия умножением):
а) 10x + 10y; д) a4 + a3;
б) 4x + 20y; е) 2x6– 4x3;
в) 9 ab + 3b; * ж) y5 + 3y6+ 4y2 ;
г) 5xy2 + 15y; * з) 5bc2 + bc.
2. Дополнительное задание.
Докажите, что значение выражения 85 – 211 делится на 17.
Вариант 3
1. Вынесите общий множитель за скобки (проверьте свои действия умножением):
а) 18ay + 8ax; д) m6 +m5;
б) 4ab - 16a; е) 5z4– 10z2;
в) – 4mn + 5n; * ж) 3x4 – 6x3+ 9x2 ;
г) 3x 2y– 9x; * з) xy2 +4xy.
2. Дополнительное задание.
Докажите, что значение выражения 792 + 79*11 делится на 30.
Вариант 4
1. Вынесите общий множитель за скобки (проверьте свои действия умножением):
а) – 7xy + 7y; д) y7 - y5;
б) 8mn + 4n; е) 16z5– 8z3;
в) – 20a2 + 4ax; * ж) 4x2 – 6x3 + 8x4;
г) 5x 2y2 + 10x; * з) xy +2xy2.
2. Дополнительное задание.
Докажите, что значение выражения 313 * 299 – 3132 делится на 7.
Cамостоятельная работа проводится в начале урока. После выполнения работы используется проверка по ключу.
Контрольная работа №1
(проводится с целью контроля знаний, умений и навыков выполнения действий над многочленами и разложения многочлена на множители способом вынесения общего множителя за скобки)
Вариант 1.
° 1. Выполните действия:
a) (7x2 – 5x + 3) – (5x2 – 4);
б) 5a2 (2a – a4).
° 2. Вынесите общий множитель за скобки:
а) 7ax – 7xb;
б) 16x2 + 12x2y.
° 3. Решите уравнение:
30 + 5(3x – 1) = 35x – 25.
4. Пассажирский поезд за 4 часа прошел такое же расстояние, какое товарный за 6 часов. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.
5. Решите уравнение:
(3x – 1)/6 – x/3 = (5 – x)/9.
Вариант 2.
° 1. Выполните действия:
a) (3y2 – 3y + 1) – (4y – 2);.
б) 4b2 (3b2+ b).
° 2. Вынесите общий множитель за скобки:
а) 8ab + 4a;
б) 18ab3 – 9a2b.
° 3. Решите уравнение:
14 + 4(5x – 2) = 44x – 30.
4. Заказ по выпуску машин должен быть выполнен по плану за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана и поэтому выполнил задание за 18 дней. Сколько машин должен был выпустить завод по плану.
5. Решите уравнение:
(x – 1)/5 = (5 – x)/2 + 3x/4.
Вариант 3.
° 1. Выполните действия:
a) (6a2 – 3a + 8) – (2a2 – 5);.
б) 3x4 (7x– x5).
° 2. Вынесите общий множитель за скобки:
а) 5xy – 15y;
б) 21a 3b2 – 14ab3.
° 3. Решите уравнение:
14 + 4(5x – 2) = 44x – 30.
4. Ученик за 8 часов работы сделал столько же деталей, сколько мастер за 5 часов. Сколько деталей в час изготовил ученик, если известно, что мастер изготовлял в час на 6 деталей больше, чем ученик?
5. Решите уравнение:
2x/3 – (2x+1)/6 = (3x – 5)/4.
Вариант 4.
° 1. Выполните действия:
a) (4b2 – 2b + 3) – (6b – 7);.
б) 6y2 (4y3+ y).
° 2. Вынесите общий множитель за скобки:
а) 6cb – 4c;
б) 24x2 y – 32x3y2.
° 3. Решите уравнение:
7x – 12 = 3(9x + 8) – 2x.
4. Рабочий должен был выполнить заказ по изготовлению деталей за 12 часов. Но он выпускал на 3 детали в час больше, чем намечалось, и поэтому выполнил заказ за 10 часов. Сколько деталей должен был изготовить рабочий?
5. Решите уравнение:
(3 – x)/3 = (x + 1)/2 – 5x/4.
Устная самостоятельная работа №10
(проводится с целью повторения правила умножения одночлена на многочлен и свойства степеней с целым показателем)
Вариант 1
1. Закончите предложение:
Чтобы умножить одночлен на многочлен, нужно …
2. Выполните умножение:
а) 3(a –4);
б) (x + 2) * 8;
3. Представьте произведение в виде степени:
а) x5 * x10;
б) a * a9;
в) y2 * yp;
г) xn * xm.
Вариант 2
1. Закончите предложение:
Чтобы умножить одночлен на многочлен, нужно …
2. Выполните умножение:
а) – 2 (a – 3);
б) (b + 4) * 5;
3. Представьте произведение в виде степени:
а) y3 * y17 ;
б) b * b10;
в) x3 * xp;
г) cn * cm.
Работа проводится в начале урока. Условие устной работы предлагается показать на компьютере. После выполнения работы используется самопроверка. Результаты обсуждаются во фронтальной беседе.
Математический диктант
Вариант 1
1. Выпишите многочлены, которые получаются, если каждый член многочлена 3x – 2 умножить на каждый член многочлена 5 – 6x2.
2. Умножить многочлен x+1 на многочлен x – 3.
3. Представьте в виде многочлена стандартного вида квадрат двучлена x – 3y.
4. Представьте в виде многочлена стандартного вида произведение двучлена x – y и трехчлена x2 + xy + y2.
5. Умножьте многочлен x – y на многочлен x + y.
Вариант 2
1. Выпишите многочлены, которые получаются, если каждый член многочлена 3 – 2y2 умножить на каждый член многочлена 2y – 1.
2. Умножить многочлен x–1 на многочлен x+ 3.
3. Представьте в виде многочлена стандартного вида квадрат двучлена a – 2b.
4. Представьте в виде многочлена стандартного вида произведение двучлена a + b и трехчлена a2 – ab + b2.
5. Умножьте многочлен a+b на многочлен a – b.
Диктант проводится в начале урока.
После выполнения диктанта используется взаимопроверка по ключу. Результаты обсуждаются во фронтальной беседе.
Самостоятельная работа
(проводится с целью формирования умений и навыков умножения многочлена на многочлен)
Вариант 1
1. Выполните умножение:
а) (a+3) (a – 7);
б) (8 + 3x) (2y – 1);
в) (a + 2) (a2 – a – 3) .
2. Упростите выражение:
а) (3a + 5) (3a – 6) +30;
б) (x – 3) (x + 5) – (x2 + 1).
3. Дополнительное задание:
Запишите вместо … такие выражения, чтобы выполнялось равенство:
3 (… + 1) = 3m + …
Вариант 2
1. Выполните умножение:
а) (x+4) (x – 5);
б) (3b + 1) (2a +7);
в) (x + 3) (x2 – x – 1) .
2. Упростите выражение:
а) (2b – 3) (5b + 7) +21;
б) (y + 3) (y – 8) – (y2 + y).
3. Дополнительное задание:
Запишите вместо … такие выражения, чтобы выполнялось равенство:
4 (… + 3) = 8m + …
Вариант 3
1. Выполните умножение:
а) (x– 4) (x+8);
б) (5a – 7) (3a + 1);
в) (2y – 1) (y2 – y + 1) .
2. Упростите выражение:
а) (7a – 2) (3a + 8) +16;
б) (2x – 5) (x + 4) – (2x2 + x).
3. Дополнительное задание:
Запишите вместо … такие выражения, чтобы выполнялось равенство:
m (…– 7) =m3 + …
Вариант 4
1. Выполните умножение:
а) (2x– 5) (x– 3);
б) (– 2 + y) (y +9);
в) (3a + 3) (a2 – a – 1) .
2. Упростите выражение:
а) (4a – 7) (2a – 5) +35;
б) (3z – 4) (z – 3) – z(3z + 1).
3. Дополнительное задание:
Запишите вместо … такие выражения, чтобы выполнялось равенство:
m2 (…– 4m) = m6 – …
Самостоятельная работа
(проводится с целью закрепления умений и навыков разложения многочлена на множители способом группировки)
Вариант 1.
1. Вынесите за скобки общий множитель:
a) a (b + c) + p (b+c);
б) a (x – 2) + (x – 2);
в) x(a – 5) + 5(5 –a).
2. Разложите многочлен px – py + 5x – 5y на множители (проверьте полученный результат умножением).
* 3. Разложите на множители:
2a + 2a2 +b + ab.
Вариант 2.
1. Вынесите за скобки общий множитель:
a) a (x – y) – b(x – y);
б) b(y+4) + (y+4) ;
в) a (b – 3) + 4(3 – b).
2. Разложите многочлен ax – ay + bx – by на множители (проверьте полученный результат умножением).
* 3. Разложите на множители:
3x + 3x2 +y + yx.
Вариант 3.
1. Вынесите за скобки общий множитель:
a) x (a – b) + y(a – b);
б) b (a +1) – (a +1);
в) x (2y – 3) – 5 (3 – 2y) .
2. Разложите многочлен ab + ac – 4b – 4c на множители (проверьте полученный результат умножением).
* 3. Разложите на множители:
3a + b + 3a2 + ab.
Вариант 4.
1. Вынесите за скобки общий множитель:
a) 2x (c – d) + y (c –d);
б) – x (y – 2) + (y – 2);
в) y (3x – 2) – (2 – 3x) .
2. Разложите многочлен ab – ac – 4b + 4c на множители (проверьте полученный результат умножением).
* 3. Разложите на множители:
3c + 3c2 – a – ac.
Самостоятельная работа проводится в конце урока и проверяется учителем.
Контрольная работа №2
(проводится с целью контроля знаний, умений, навыков умножения многочлена на многочлен и разложения многочлена на множители способом группировки)
Вариант 1.
° 1. Представьте в виде многочлена:
а) (y – 4) (y + 5);
б) (3a + 2b) (5a – b);
в) (x – 3) (x2 + 2x – 6).
° 2. Разложите на множители:
а) b (b+1) – 3(b +1);
б) ca – cb + 2a – 2b.
3. Упростите выражение:
(a2 – b2) (2a + b) – ab (a+b).
4. Докажите тождество:
(x – 3) (x+4) = x (x +1) – 12.
5. Решите задачу:
Ширина прямоугольника вдвое меньше его длины. Если ширину увеличить на 3 см, а длину увеличить на 2 см, то площадь его увеличится на 78 см2. Найти длину и ширину прямоугольника.
Вариант 2.
° 1. Представьте в виде многочлена:
а) (x + 7) (x – 2);
б) (4c – d) (6c + 3d);
в) (y +5) (y2 – 3y +8).
° 2. Разложите на множители:
а) y (a–b) + 2(a –b);
б) 3x – 3y +ax – ay.
3. Упростите выражение:
xy (x +y) – (x2 + y2) (x – 2y).
4. Докажите тождество:
a (a – 2) – 8 = (a + 2) (a – 4).
5. Решите задачу:
Длина прямоугольника на 12 дм больше его ширины. Если длину увеличить на 3 дм, а ширину увеличить на 2 дм, то площадь его увеличится на 80дм2. Найти длину и ширину прямоугольника.
Вариант 3.
° 1. Представьте в виде многочлена:
а) (a – 3) (a + 6);
б) (5x – y) (6x + 4y);
в) (b – 2) (b2 + 3b – 8).
° 2. Разложите на множители:
а) c (d – 5) +6(d–5);
б) bx – by + 4x – 4y.
3. Упростите выражение:
(c2 + d2) (c + 3d) – cd (3c – d).
4. Докажите тождество:
(y – 5) (y+7) = y (y +2) – 35.
5. Решите задачу:
Ширина прямоугольника на 6см меньше его длины. Если ширину увеличить на 5 см, а длину увеличить на 2 см, то площадь его увеличится на 110 см2. Найти длину и ширину прямоугольника.
Вариант 4.
° 1. Представьте в виде многочлена:
а) (b + 8) (b – 3);
б) (6p – q) (3p +5q);
в) (a + 4) (a2 – 6a + 2).
° 2. Разложите на множители:
а) a (x+y) – 5(x +y);
б) 5a – 5b + da – db.
3. Упростите выражение:
mn (m – n) – (m2 – n2) (2m + n).
4. Докажите тождество:
b (b – 4) – 18 = (b +3) (b – 6).
5. Решите задачу:
Длина прямоугольника в 3 раза больше его ширины. Если длину увеличить на 2 м, а ширину увеличить на 3 м, то площадь его увеличится на 72 см2. Найти длину и ширину прямоугольника.
Примечание. Задания, отмеченные знаком ° соответствуют обязательному уровню обучения.
Тест
по теме: Многочлены
Вариант 1
| №п/п | Задание | Варианты ответов |
| 1 | Приведите подобные члены многочлена 2y2 – 3y – y2 +2y | А. 2y2 – 2y; Б. 3y2 – 3y; В. y2 – y; Г. 3y2 + 5y. |
| 2 | Раскройте скобки (3 – 5a) – (2b – 2c) | А. 3 – 5a +2b +2c; Б. 3 – 5a – 2b +2c; В. 3 – 5a – 2b– 2c; Г. 3 +5a +2b – 2c. |
| 3 | Выполните умножение 2a (a2 +a +1) | А. 2a2 +2a + 2; Б. 2a3 +2a + 2; В. 2a3 +2a2 + 2; Г. 2a2 +2a + 1. |
| 4 | В виде какого произведения можно представить выражение ab – 5b2 | А. a (b +5b2); Б. a (b –5b2); В. b (a +5b); Г. b(a–5b). |
| 5 | Раскройте скобки (2a + 1) (a – 2) | А. 2a2 + 5a – 2; Б. 2a2 – 3a – 2; В. 2a2 – 3a + 2; Г. 2a2 +5a +2. |
| 6 | В виде какого произведения можно записать выражение x(b + c) + 4b + 4c | А. (b + c) (x +4); Б. 4 (b +c); В. x (b +c); Г. 4x (b + c) . |
| 7 | Решите уравнение 4(3x – 2) = 5x – 2 | А. 7/6; Б. – 6/7; В. 6/7; Г. – 7/6 . |
| 8 | В виде какого выражения можно записать периметр прямоугольника ABCD 1. 2(m+n)+2(a+b+c); D C  2. (a+b+c)(m+n); m 2. (a+b+c)(m+n); m
3. 2(m+n+a+b+c). n A a b c B | А. Только в виде выражения 3; Б. В виде выражения 2; В. Только в виде выражения 1; Г. В виде выражения 1 и 3. |
|
| Код правильных ответов | B Б В Г А А В Г |
Тест
по теме: Многочлены
Вариант 2
| №п/п | Задание | Варианты ответов |
| 1 | Приведите подобные члены многочлена 3x2 – 4x – 5x2 +7x | А. 2x2 + 11x; Б. – 2x2 + 3x; В. –2x2 – 11x; Г. 2x2 – 11x. |
| 2 | Раскройте скобки (8x – 3) – (4y + 5z) | А. 8x – 3 + 4y +5z; Б. 8x – 3 – 4y +5z; В. 8x – 3 – 4y – 5z; Г. 8x + 3 – 4y – 5z. |
| 3 | Выполните умножение – 3x (x2 – x +1) | А. – 3x3 +3x2 – 3x; Б. – 3x3 +3x2 – 3x; В. – 3x2 +3x – 3; Г. – 3x3 –3x2 + 3x. |
| 4 | В виде какого произведения можно представить выражение x2y – xy2 | А. x2 y (1 – y); Б. x y (x + y); В. x y2 (x – 1); Г. x y (x – y). |
| 5 | Раскройте скобки (4x – 5) (2 – 3x) | А. 12x2 + 23x – 10; Б. – 12x2 + 23x – 10; В. 12x2– 23x + 10; Г. – 12x2 + 23x – 10. |
| 6 | В виде какого произведения можно записать выражение ab + ac – 4b – 4c? | А. (b + c) (x +4); Б. (b + c) a – 4); В. (b–c) (a +4); Г.(b – c) (a – 4) . |
| 7 | Решите уравнение 3(2x – 1) = 2x – 6 | А. 3/4; Б. 4/3; В. – 3/4; Г. – 4/3 .
|
| 8 | В виде какого выражения можно записать площадь прямоугольника ABCD? 1. (an+am+ ap) + (bn+bm + bp); D C  2. (m + n– p) (a + b); а 2. (m + n– p) (a + b); а
3. (m + n+ p) (a+b). b A m n p B | А. Только в виде выражения 1; Б. В виде выражения 1 и 2; В. Только в виде выражения 2; Г. В виде выражения 1 и 3. |
|
| Код правильных ответов | Б В А Г Б Б В Г |
Баллы по заданиям
1 – 1 балл
2 – 1 балл
3 – 1 балл
4 – 1 балл
5 – 2 балл
6 – 1 балл
7 – 2 балл
8 – 3 балл
Итоговая шкала
12 баллов – «5»
10-11 баллов – «4»
6 – 9 баллов – «3»
Менее 6 баллов – «2»
Тест проводится на обобщающем уроке и проверяется учителем.
По теме: Многочлены можно провести зачетную работу.
Карточки к зачету по теме: «Многочлены»
(проводится с целью итогового контроля по теме)
Карточка № 1
Обязательная часть
1. Сформулируйте правило умножения одночлена на многочлен.
2. Сформулируйте определение многочлена.
3. На примере многочлена 3a2 b + 2ab2 – 4ab * 5a объясните, как привести многочлен к стандартному виду.
3. а) Разложите на множители:
1) 12x3 y – 4x;
2) 6a – 6b + am – bm.
б) Решите уравнение:
3 (y + 2) – 5 = 3y + 1.
Дополнительная часть
1. Решите уравнение:
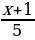 –
– 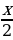 = 2.
= 2.
2. Решите задачу:
Чтобы выполнить заказ в срок, токарь должен был изготовлять по 6 деталей в час. Изготавливая по 8 деталей в час, он выполнил задание на 2 часа раньше срока. Сколько деталей должен был изготовлять токарь?
Карточка № 2
Обязательная часть
1. Сформулируйте правило умножения одночлена на многочлен.
2. На примере многочлена 14ax2 + 7ax объясните, как выполняется разложение многочлена на множители с вынесением общего множителя за скобки.
3. а) Выполните действия:
1) (2b2 – 3b + 4) – (5b – 2);
2) (x +5) (x – 3).
б) Решите уравнение:
14 + 2(5x – 1) = 2.
Дополнительная часть
1. Решите уравнение:
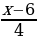 –
– 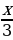 = 1.
= 1.
2. Решите задачу:
На путь от поселка до станции автомобиль потратил на 1 час меньше, чем велосипедист? Найдите расстояние от поселка до станции, если автомобиль проехал его со средней скоростью 70 км/ч, а велосипедист – 20 км/ч?
Карточка № 3
Обязательная часть
1. Какое преобразование называется разложением многочлена на множители?
2. На примере многочлена 5x5y – 15x4y объясните, как выполняется разложение многочлена на множители с вынесением общего множителя за скобки.
3. а) Выполните действия:
1) 7x4 (2x3 + x);
2) (y +2) (y – 3).
б) Решите уравнение:
3 – 5 (x + 1) = 6 – 4x.
Дополнительная часть
1. Решите уравнение:
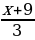 –
– 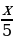 = 1.
= 1.
2. Решите задачу:
Все имеющиеся яблоки можно разложить в 5 пакетов или в 5 коробок. Сколько килограммов яблок имеется, если в пакет помещается на 3 кг яблок больше, чем в коробку?
Карточка № 4
Обязательная часть
1. Что называется степенью многочлена? Приведите пример многочлена третьей степени.
2. На примере многочлена 8x + ay + 8y + ax объясните, как выполняется разложение многочлена на множители способом группировки.
3. а) Выполните действия:
1) (3b2 – 2b + 7) – (5b – 4);
2) 3x2 (5x + 3).
б) Решите уравнение:
(2x – 13) – (5x + 1) = 15.
Дополнительная часть
1. Решите уравнение:
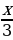 –
– 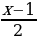 = 4.
= 4.
2. Решите задачу:
Ширину прямоугольника увеличили на 4 см и получили квадрат, площадь которого больше площади прямоугольника на 32см2. Найдите сторону квадрата?
Карточка № 5
Обязательная часть
1. Сформулируйте правило умножения многочлена на многочлен.
2. Сформулируйте правило заключения многочлена в скобки, перед которыми стоит знак «+» или знак «–».
В многочленах 6y3 – y + 7 и 8x6 + x – 5 заключите в скобки два последних члена, поставив перед скобками:
а) знак « + »;
б) ) знак « – ».
3. а) Разложите на множители:
1) 5 m2n – 20 mn2;
2) ab2 + a2b – 13a – 13b.
б) Решите уравнение:
10x - 5 = 6 (8x + 3) – 5x.
Дополнительная часть
1. Решите уравнение:
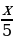 –
– 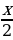 = – 3.
= – 3.
2. Решите задачу:
Двое рабочих изготовили по одинаковому количеству деталей. Первый выполнил эту работу за 6 часов, а второй - за 4 часа, так как каждый час изготовлял на 10 деталей больше первого. Сколько деталей изготовил каждый рабочий?
Пояснение. Задачи на зачетах можно решать кратко.






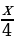 +
+ 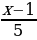 = 6
= 6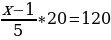 ,
,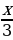 +
+ 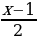 = 4
= 4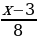 = 1
= 1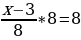 ,
,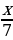 +
+ 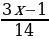 = 2
= 2
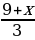 –
–  2. (a+b+c)(m+n); m
2. (a+b+c)(m+n); m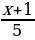 –
– 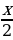 = 2.
= 2.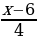 –
– 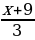 –
– 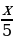 = 1.
= 1.









