Россия, Калтасиснкий район с.Краснохолмский
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 22.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 04.12.2024 19:47
Возжаева Светлана Юрьевна
учитель математики
36 лет
14 499
2 454 
Местоположение
Специализация
Шар. сечение шара плоскостями
Категория:
Геометрия
16.05.2020 15:04
Просмотр содержимого документа
«Шар. сечение шара плоскостями»
Шар. Сечение шара плоскостями.
Шар или
сфера?
Шар.
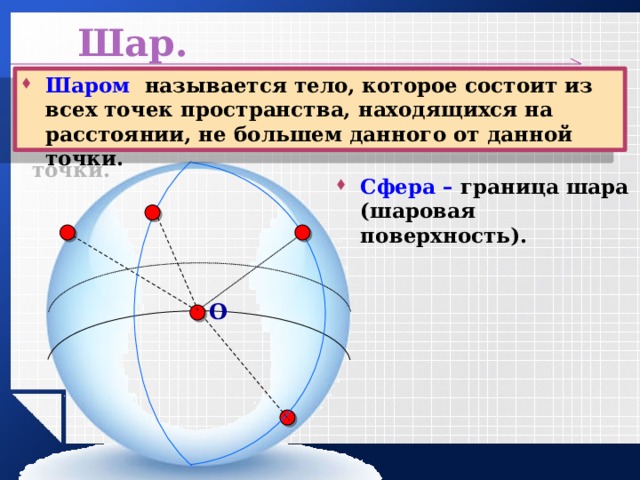
- Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного от данной точки.
- Сфера – граница шара (шаровая поверхность).
O
Шар.
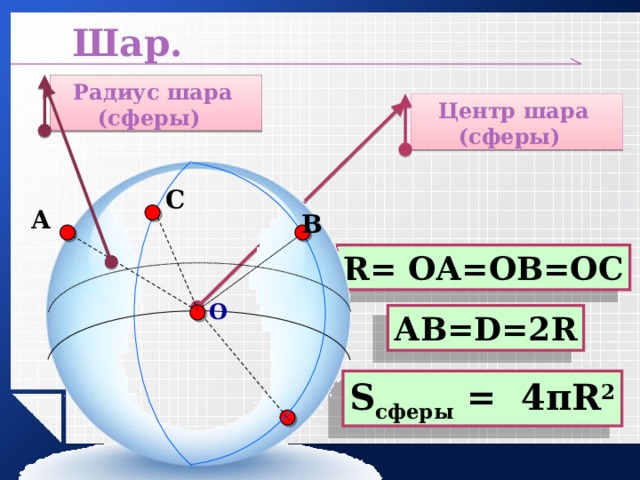
Радиус шара (сферы)
Центр шара (сферы)
С
А
В
R= ОА=ОВ=ОС
O
АВ=D=2R
S сферы = 4πR 2
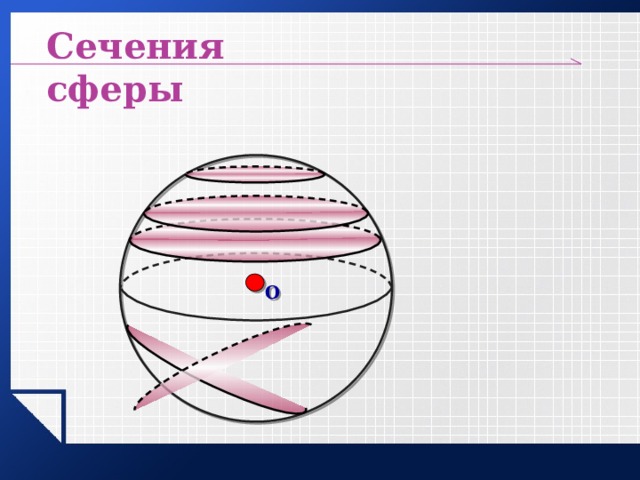
Сечения сферы
O
Шар.
Теорема: Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра опущенного из центра шара на секущую плоскость
О
А
В
С
Плоскость проходящая через центр шара называется диаметральной.
R, то шар (сфера) и плоскость не имеют общих точек О R d ОМ ┴ α; ОМ = d М " width="640"
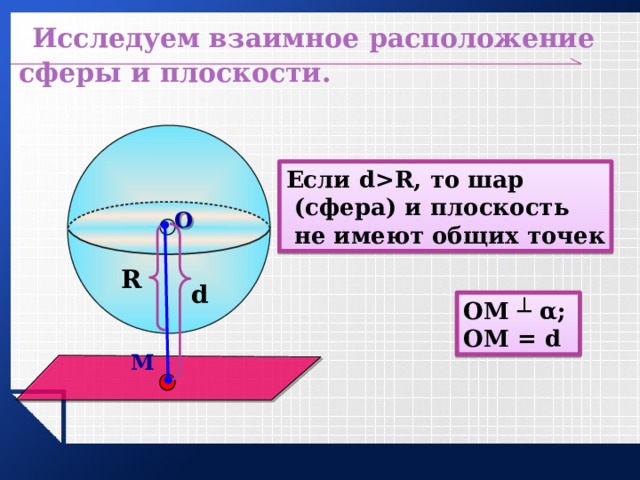
Исследуем взаимное расположение сферы и плоскости.
Если dR, то шар
(сфера) и плоскость
не имеют общих точек
О
R
d
ОМ ┴ α;
ОМ = d
М
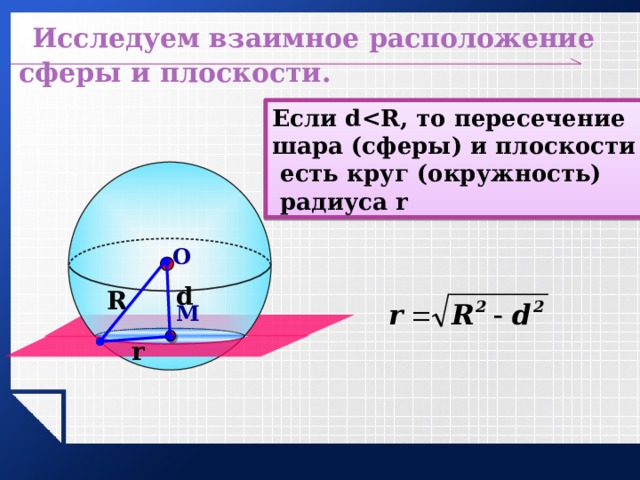
Исследуем взаимное расположение сферы и плоскости.
Если d
шара (сферы) и плоскости
есть круг (окружность)
радиуса r
О
d
R
М
r
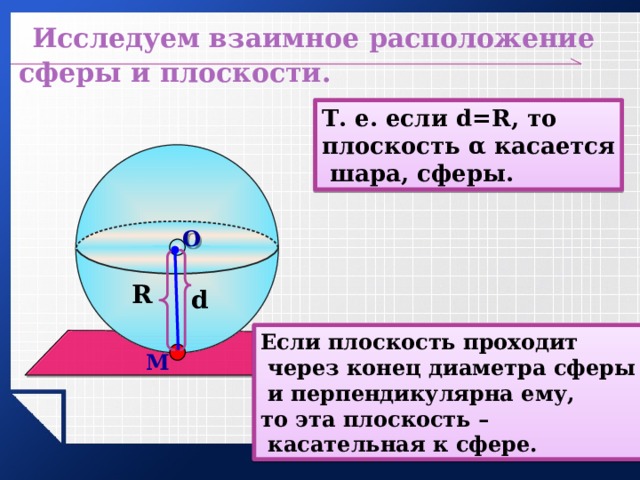
Исследуем взаимное расположение сферы и плоскости.
Т. е. если d=R, то
плоскость α касается
шара, сферы.
О
R
d
Если плоскость проходит
через конец диаметра сферы
и перпендикулярна ему,
то эта плоскость –
касательная к сфере.
М
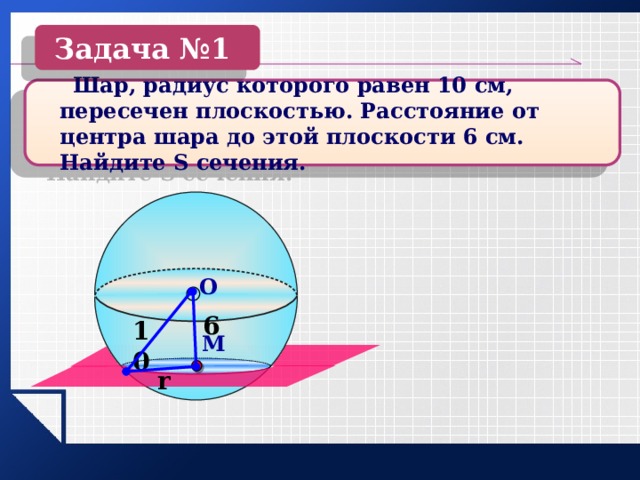
Задача №1
Шар, радиус которого равен 10 см, пересечен плоскостью. Расстояние от центра шара до этой плоскости 6 см. Найдите S сечения.
О
6
10
М
r
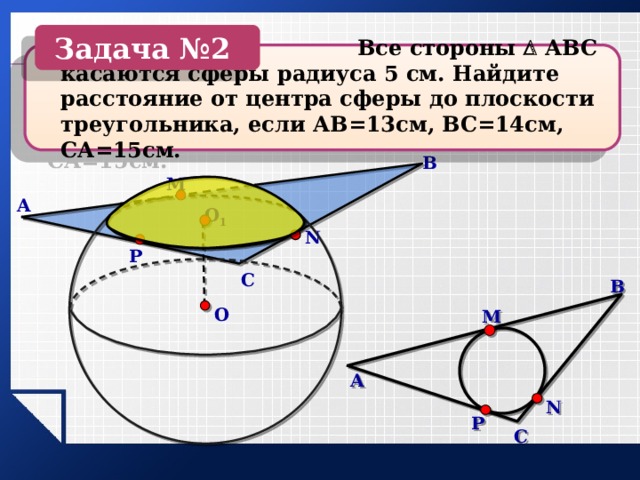
Задача №2
Все стороны АВС касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ=13см, ВС=14см, СА=15см.
B
М
A
O 1
N
P
C
B
O
М
A
N
P
C
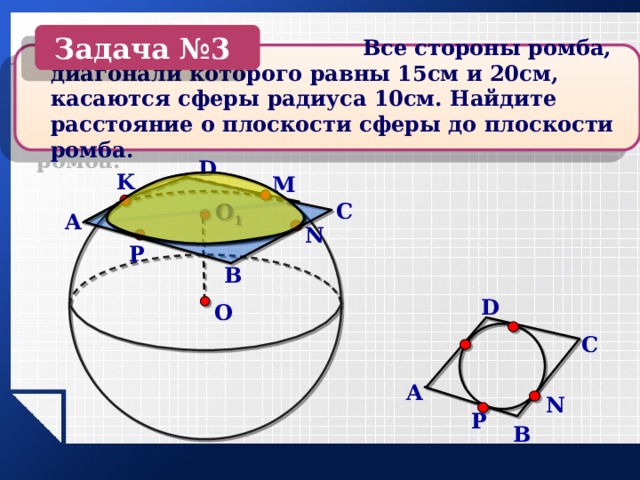
Задача №3
Все стороны ромба, диагонали которого равны 15см и 20см, касаются сферы радиуса 10см. Найдите расстояние о плоскости сферы до плоскости ромба.
D
K
M
C
O 1
A
N
P
B
D
O
C
A
N
P
B
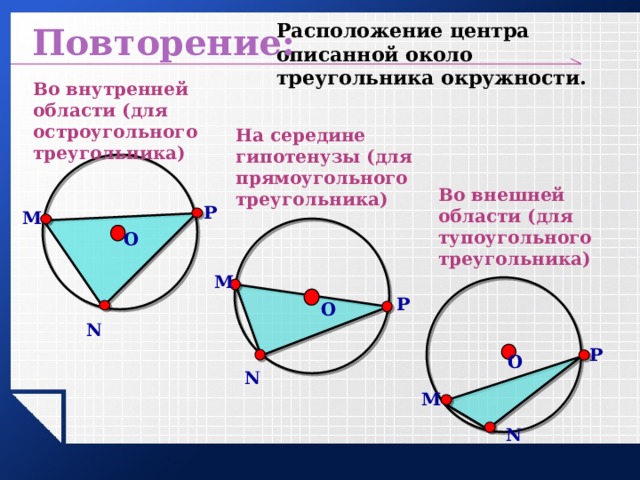
Повторение:
Расположение центра описанной около треугольника окружности.
Во внутренней области (для остроугольного треугольника)
На середине гипотенузы (для прямоугольного треугольника)
Во внешней области (для тупоугольного треугольника)
P
М
O
М
P
O
N
P
O
N
М
N
гипотенуза
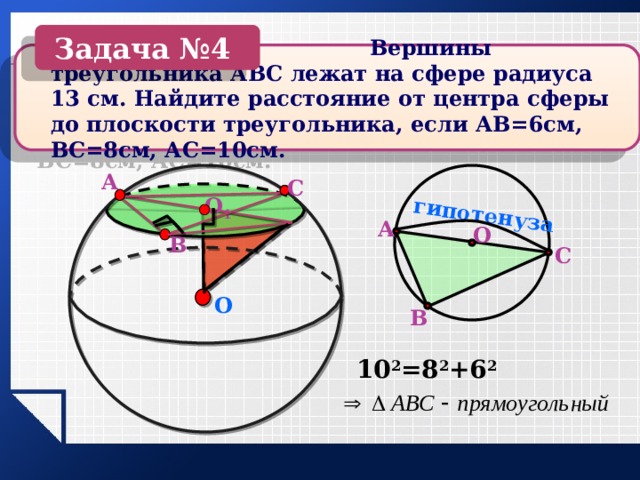
Задача №4
Вершины треугольника АВС лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ=6см, ВС=8см, АС=10см.
А
С
O 1
А
O
В
С
O
В
10 2 =8 2 +6 2
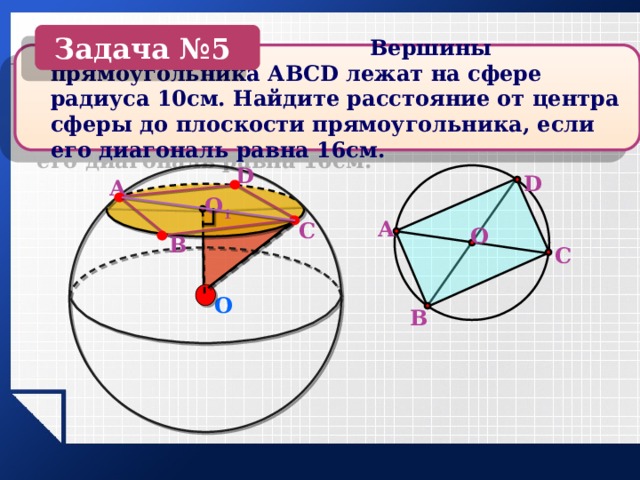
Задача №5
Вершины прямоугольника АВСD лежат на сфере радиуса 10см. Найдите расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16см.
D
D
А
O 1
А
С
O
В
С
O
В
Домашнее задание:
© 2020, Возжаева Светлана Юрьевна 1607 13
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
