Симметрия в алгебре

Симметрия в алгебре

Выполнила: Галиева Анастасия 9 В

Учитель: Иванченко Ирина Алексеевна

Цели и задачи

Цель:

• Рассмотреть, как симметрия используется в школьном курсе алгебры

Задачи:

• Познакомиться с понятием «симметрия»
• Научиться различать виды симметрии
• Понять, как симметрия используется в алгебре

Симметрия

Симметрия (от греч. symmetria — соразмерность) пропорциональность, соразмерность в расположении частей целого в пространстве, полное соответствие (по расположению, величине) одной половины целого другой половине.

Виды симметрии

Рассмотрим три основных вида симметрии:

• центральная симметрия
• осевая симметрия
• зеркальная симметрия

Центральная симметрия

Симметрию относительно точки называют центральной симметрией.

Например: точки M и M1 симметричны относительно некоторой точки O , если точка O является серединой отрезка MM1. Точка O называется центром симметрии.

Осевая симметрия

Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Например: точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.

Зеркальная симметрия

Зеркальная симметрия-это отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно плоскости а.

Примеры числовых симметрий

В записи чисел: 101,1221,67076 и т.д.

Симметрия в выражениях:

(a+b)²=a²+2ab+b²

(a+b ) 3 =(a+b)(a²+2ab+b²)

Палиндроматика:

41-23=32-14 74-65=56-47

75+68=86+57 42+35=53+24

Симметрические уравнения

Симметрические уравнения

Пример 1

Пример 2

Симметрические уравнения

Другие примеры симметрических уравнений:

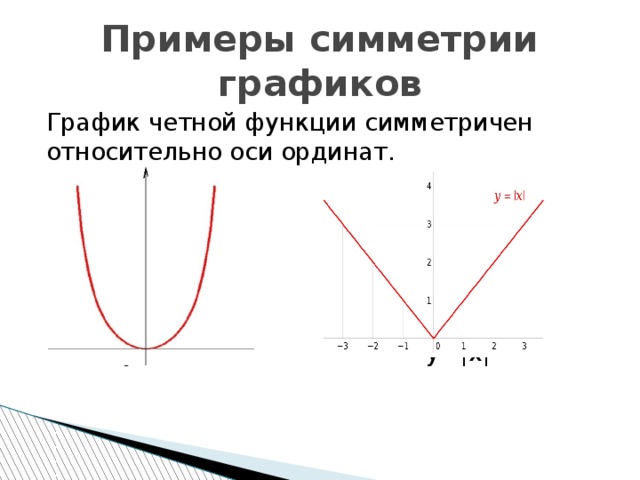
Примеры симметрии графиков

График четной функции симметричен относительно оси ординат.

у=х² у=|х|

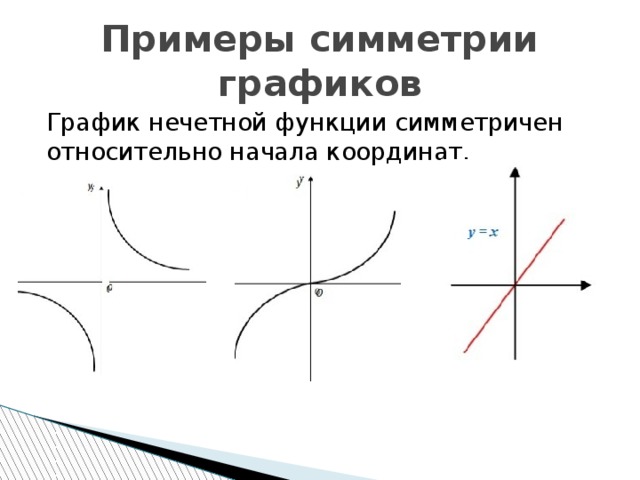
Примеры симметрии графиков

График нечетной функции симметричен относительно начала координат.

Вывод

Симметрия в широком смысле-это неизменность при каких либо преобразованиях. Математики издавна стремились к красоте математических формул и справедливо считали, что красивая формула отличается от некрасивой тем, что в красоте больше симметрии. И такие «красивые» формулы не только делают преобразования красивыми, но и значительно облегчают вычислительную работу

Источники

• https:// multiurok.ru/index.php/files/simmietriia-v-alghiebrie-matierial-k-priezientatsii.html
• http://www.myshared.ru/slide/1216506 /
• https:// infourok.ru/simmetriya-v-algebre-prezentaciya-1209355.html
• https:// www.yaklass.ru

Спасибо за внимание!