Просмотр содержимого документа
«Симметрия. Осевая и центральная.»

Урок по геометрии
в 8 классе
Симметрия.
Осевая и центральная
симметрии
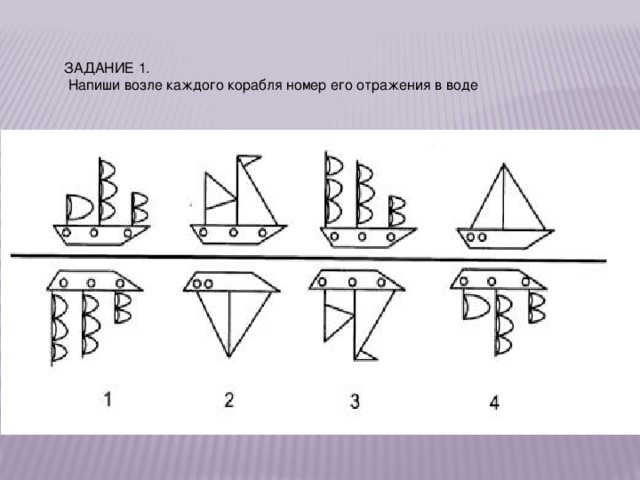
ЗАДАНИЕ 1.
Напиши возле каждого корабля номер его отражения в воде

Слово «симметрия» греческого происхождения («сим» - с, «метрон» - мера) и буквально означает «соразмерность».
Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство.
Герман Вейль .

Дорисуй предметы так, чтобы они стали симметричными относительно данной прямой

Фигуры, обладающие
осевой симметрией

а
Две точки и называются симметричными относительно прямой а, если эта прямая проходит через середину через середину отрезка и перпендикулярна к нему.
Прямая а называется осью симметрии.

Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры.
а

Буквы, имеющие
горизонтальную ось симметрии
В Е Ж З К Н О С Ф Х Э Ю

Буквы, имеющие
вертикальную ось симметрии
А Д Ж Л М Н О П Т Ф Х Ш

Буквы, не имеющие
ось симметрии
Б Г И Р У Ц Ч Я Щ

Симметрия широко распространена в природе

Издавна человек использовал симметрию
в архитектуре

Здание МГУ
Здание Большого театра в Москве
им. М. В. Ломоносова

Многие атомы располагаются в
пространстве по принципу симметрии
магний
железо
медь
Кристаллы блещут симметрией
Е. С. Федоров (кристаллограф)

Две точки и называются симметричными относительно точки О, если О – середина отрезка .
Точка О – называется центром симметрии

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры.

































