ГЕОМЕТРИЯ.
УРОК: «Контрольная работа № 1«Метод координат». Синус, косинус и тангенс угла. Основное тригонометрическое тождество. Формулы приведения»
Учитель: Васильева О.В.
Класс: 9
Цель урока:
- образовательная: ввести понятия синуса, косинуса и тангенса угла, актуализировать знания о синусе, косинусе и тангенсе угла в прямоугольном треугольнике, ознакомить с основным тригонометрическим тождеством, формулами приведения и формулой для нахождения координат точки, научить применять их при решении задач;
- развивающая: развитие внимания, памяти, речи, логического мышления, самостоятельности;
- воспитательная: воспитание дисциплины, наблюдательности, аккуратности, чувства ответственности.
Ход урока:
Организационный момент.
Актуализация знаний. Контрольная работа № 1«Метод координат».
Изучение нового материала
Учитель: сегодня мы приступаем к изучению новой главы «Соотношение между сторонами и углами треугольника. Скалярное произведение векторов» и первой темой в данной главе будет «Синус, косинус и тангенс угла». Запишите в тетрадях число и тему урока
Запись в тетрадях:
Число. Тема урока: Синус, косинус и тангенс угла.
Учитель: но прежде, чем перейти к изучению этой темы, выведем с вами определения
синус острого угла α прямоугольного треугольника – это отношение противолежащего катета к гипотенузе.
Косинус острого угла α прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.
Учитель: теперь решите следующий пример
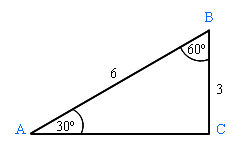
1. Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.
Выясним синус угла А и косинус угла В.
Решение
1) Сначала находим величину угла В. Тут все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º – 30º = 60º.
2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:
sin A = 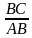 =
= 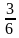 =
= 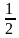 .
.
3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:
cos B = 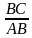 =
= 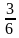 =
= 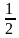 .
.
В итоге получается:
sin A = cos B = 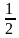 .
.
Или:
sin 30º = cos 60º = 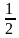 .
.
Теперь мы познакомимся с этими понятиями в независимости от фигуры, в которой они находятся. (презентация)
Введем прямоугольную систему координат Оху и построим полуокружность радиуса 1 с центром в начале координат, расположенную в первом и втором квадрантах. Данная полуокружность называется единичной (см. рис. 290 в учебнике). Запишите определение с экрана и сделайте рисунок. (слайд 3)
Запись в тетрадях:
Полуокружность называется единичной, если ее центр находится в начале координат, а радиус равен 1.
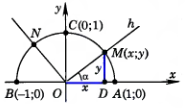
Учитель: из точки О проведем луч h , пересекающий единичную полуокружность в точке М (х;у). обозначит буквой угол между лучом h и положительной полуосью абсцисс. Если луч h совпадает с положительной полуосью абсцисс, то будем считать, что = 0 .
Если угол острый, то из прямоугольного треугольника DOM имеем, sin = 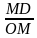 , a cos =
, a cos = 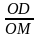 .
.
Но OM = 1, MD это ордината, OD - абсцисса, поэтому sin ордината у точки М, cos это абсцисса х точки М.
Запись на доске и в тетрадях:
Если угол острый, то из прямоугольного треугольника DOM имеем,
sin = 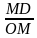 , a cos =
, a cos = 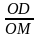 .
.
Но OM = 1, MD = y, OD = x,
поэтому sin = y, cos = x. (1)
Учитель: Так как из прямоугольного треугольника DOM тангенс - это отношение противолежащего катета к прилежащему tg = 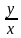 , то тангенс будет равен отношению синуса угла к косинусу угла tg =
, то тангенс будет равен отношению синуса угла к косинусу угла tg = 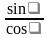 . Существует еще функция, обратная тангенсу - катангенс, и он равен отношению косинуса угла к синусу ctg =
. Существует еще функция, обратная тангенсу - катангенс, и он равен отношению косинуса угла к синусу ctg = 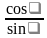 .
.
Итак, синус острого угла равен ординате у точки М, а косинус угла - абсциссе х точки М. Запишите со слайда информацию в тетради (слайд 4).
Запись на доске и в тетрадях:
Т.к. tg = 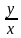 , то tg =
, то tg = 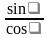 , ctg =
, ctg = 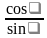 .
.
Учитель: если угол прямой, тупой или развернутый, это углы AOC, AON и AOB или = 0 , то синус и косинус угла также определим по формулам (1).
Таким образом, для любого угла из промежутка 0 ≤ ≤ 180 синусом угла называется ордината у точки М, косинусом угла - абсцисса х точки М.
Так как координаты (х; у) точек единичной полуокружности заключены в промежутках 0 ≤ у ≤ 1, - 1 ≤ х ≤ 1, то для любого из промежутка 0 ≤ ≤ 180 справедливы неравенства:
0 ≤ sin ≤ 1, - 1≤ cos ≤ 1 (слайд 5). Запишите это в тетради.
Запись в тетрадях:
Т.к. 0 ≤ у ≤ 1, - 1 ≤ х ≤ 1, то для любого из промежутка 0 ≤ ≤ 180
0 ≤ sin ≤ 1, - 1≤ cos ≤ 1.
Учитель: а теперь найдем значения синуса и косинуса для углов 0, 90 и 180. Для этого рассмотрим лучи OA, OC и OB, соответствующие этим углам (см.рис.290). Так как точки А, С и B имеют координаты А (1; 0), С (0; 1), В (-1; 0), то
Sin 0 = 0, sin 90 = 1, sin 180 = 0, cos 0 = 1, cos 90 = 0, cos 180 = - 1. (2) (слайд 6) Запишите в тетради.
Запись в тетрадях:
Sin 0 = 0, sin 90 = 1, sin 180 = 0, cos 0 = 1, cos 90 = 0, cos 180 = - 1
Учитель: кроме этих значений при решении задач вам понадобятся и другие значения синуса, косинуса, тангенса и катангенса при различных угла . Сделайте себе в тетради небольшую тригонометрическую таблицу значений синуса, косинуса, тангенса и катангенса
Запись в тетрадях:
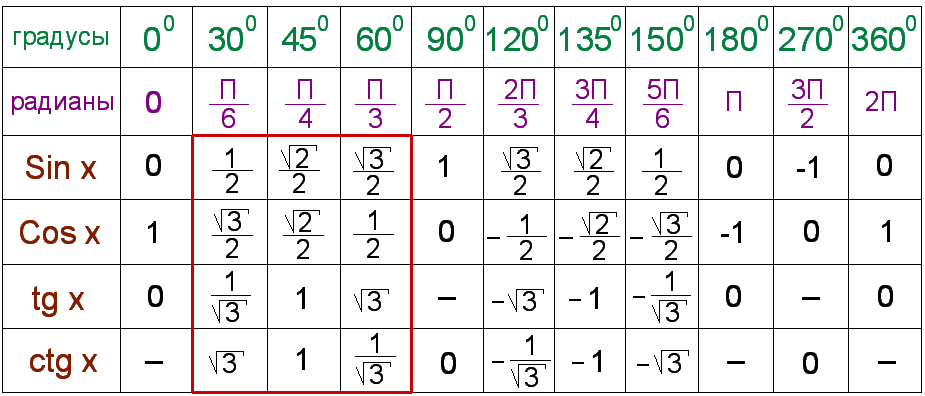
Учитель: теперь мы познакомимся с вами с основным тригонометрическим тождеством. Запишите заголовок в тетради.
Запись в тетрадях:
Основное тригонометрическое тождество.
sin2 + cos2 = 1, (4)
Которое выполняется для любого угла из промежутка 0 ≤ ≤ 180. Равенство (4) называется основным тригонометрическим тождеством. В VIII классе оно было доказано для острых углов. Запишите в тетради информацию со слайда.
Запись в тетрадях:
Для любого угла из промежутка 0 ≤ ≤ 180 верно
sin2 + cos2 = 1 - основное тригонометрическое тождество.
Учитель: теперь определим знаки синуса, косинуса и тангенса в разных четвертях.
Знаки синуса.
Так как sin = 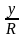 , то знак синуса зависит от знака у. В первой и второй четвертях у 0, в третьей и четвертой у 0. Значит синус больше нуля, если угол находится в первой ил второй четверти, и синус меньше нуля, если угол находится в третьей ил четвертой четверти. Запишите эту информацию в тетради со слайда (слайд 10)
, то знак синуса зависит от знака у. В первой и второй четвертях у 0, в третьей и четвертой у 0. Значит синус больше нуля, если угол находится в первой ил второй четверти, и синус меньше нуля, если угол находится в третьей ил четвертой четверти. Запишите эту информацию в тетради со слайда (слайд 10)
Запись в тетрадях:
т.к. sin = 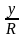 ,
,
I , II ч - sin 0, III, IV ч - sin
Учитель: знаки косинуса. Так как cos = 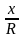 , то знак косинуса зависит то знака х. тогда в первой и четвертой четвертях х 0, а во второй и третьей четвертях x находится в первой или четвертой четверти, и косинус является меньше нуля, если угол находится во второй или третьей четверти. Запишите это в тетради со слайда.
, то знак косинуса зависит то знака х. тогда в первой и четвертой четвертях х 0, а во второй и третьей четвертях x находится в первой или четвертой четверти, и косинус является меньше нуля, если угол находится во второй или третьей четверти. Запишите это в тетради со слайда.
Запись в тетрадях:
Так как cos = 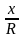
I , IV ч - cos a 0, II, III ч - cos a
Учитель: знаки тангенса и катангенса.
Так как tg = 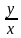 , а ctg =
, а ctg =  , то знаки tg и ctg зависят от знаков x и y. В 1 и 3 четвертях x и y имеют одинаковые знаки, а во 2 и 4 разные. Значит: tg 0 и ctg 0, если угол является углом 1 или 3 четверти; tg является углом 2 или 4 четверти. Запишите в тетради, и перенесите в таблицу.
, то знаки tg и ctg зависят от знаков x и y. В 1 и 3 четвертях x и y имеют одинаковые знаки, а во 2 и 4 разные. Значит: tg 0 и ctg 0, если угол является углом 1 или 3 четверти; tg является углом 2 или 4 четверти. Запишите в тетради, и перенесите в таблицу.
Запись в тетрадях:
tg a = 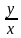
I , III ч - tg a 0, II, IV ч - tg a
ctg = 
I , III ч - ctg a 0, II, IV ч - ctg a
Учитель: кроме основное тригонометрического тождества справедливы также следующие тождества, которые являются формулами приведения. Запишите их в тетради.
sin (90 - ) = cos
cos (90 - ) = sin (5) при 0 ≤ ≤ 90,
sin (180 - )= sin
cos (180 - ) = - cos (6) при 0 ≤ ≤ 180 .
Запись в тетрадях:
Формулы приведения.
sin (90 - ) = cos
cos (90 - ) = sin (5) при 0 ≤ ≤ 90 ,
,
sin (180 - )= sin
cos (180 - ) = - cos (6) при 0 ≤ ≤ 180 .
.
Учитель: и последнее, что мы сегодня с вами рассмотрим, это формулы для вычисления координат точки, сделайте в тетрадях следующий заголовок: формулы для вычисления координат точки. (слайд 12)
Запись в тетрадях:
Формулы для вычисления координат точки.
Учитель: итак, пусть задана система координат Оху и дана произвольная точка А(х;у) с неотрицательной ординатой у (см.рис. 291 учебника).
Выразим координаты точки А через длину отрезка ОА и угол между лучом ОА и положительной полуосью Ох. Для этого обозначим буквой М точку пересечения луча ОА с единичной полуокружностью. По формулам sin = y, cos = x координаты точки М соответственно равны cos и sin . Вектор  имеет те же координаты, что и точка М, т.е.
имеет те же координаты, что и точка М, т.е.  (cos ; sin ). Вектор
(cos ; sin ). Вектор  имеет те же координаты, что и точка А, т.е.
имеет те же координаты, что и точка А, т.е.  (х; у). По лемме о коллинеарных векторах
(х; у). По лемме о коллинеарных векторах  = ОА ∙
= ОА ∙  , поэтому
, поэтому
x = ОА ∙ cos ,
y = OA ∙ sin . (7)
Запишите все в тетрадь со слайда.
Запись в тетрадях:
sin = y, cos = x
М(cos ; sin ),  (cos ; sin ),
(cos ; sin ),  (х; у).
(х; у).
По лемме о коллинеарных векторах  = ОА ∙
= ОА ∙  , поэтому
, поэтому
x = ОА ∙ cos ,
y = OA ∙ sin . (7)
4. Закрепление изученного материала
Учитель: а теперь закрепим изученный материал при решении следующих задачах:
К доске вызываются ученики.
Запись на доске и в тетрадях:
№ 1013 (а, б)
Дано: а) cos = 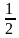 . б) cos =
. б) cos =  . Найти: sin
. Найти: sin
Ученик: так как угол находится во 2 ч., то sin 0
Запись на доске и в тетрадях:
Так как находится во 2 ч., то sin 0, sin =  .
.
Дано: а) cos = 1; в) sin =  и 0 .
и 0 .
5. Подведение итогов урока и домашнее задание
Учитель: итак, сегодня на уроке мы изучили синус, косинус и тангенс угла. Теперь ответьте на следующие вопросы:
Что называется синусом угла? косинусом угла?
что такое тангенс угла? катангенс угла?
какое основное тригонометрическое тождество вы знаете?
какие есть формулы для вычисления координат точки?
Ученик: x = ОА ∙ cos , y = OA ∙ sin .
как определить знаки синуса или косинуса?
Ученик: нужно определить, в какой четверти лежит точка с заданными координатами, или данный угол .
Запись на доске и в тетрадях:
Д/з: §1, пп. 93 - 95, №№ 1014, 1015 (б, г)
Учитель: урок окончен. До свидания.








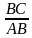 =
= 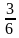 =
= 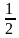 .
.
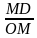 , a cos =
, a cos = 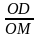 .
. 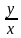 , то тангенс будет равен отношению синуса угла к косинусу угла tg =
, то тангенс будет равен отношению синуса угла к косинусу угла tg = 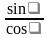 . Существует еще функция, обратная тангенсу - катангенс, и он равен отношению косинуса угла к синусу ctg =
. Существует еще функция, обратная тангенсу - катангенс, и он равен отношению косинуса угла к синусу ctg = 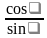 .
.
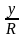 , то знак синуса зависит от знака у. В первой и второй четвертях у 0, в третьей и четвертой у 0. Значит синус больше нуля, если угол находится в первой ил второй четверти, и синус меньше нуля, если угол находится в третьей ил четвертой четверти. Запишите эту информацию в тетради со слайда (слайд 10)
, то знак синуса зависит от знака у. В первой и второй четвертях у 0, в третьей и четвертой у 0. Значит синус больше нуля, если угол находится в первой ил второй четверти, и синус меньше нуля, если угол находится в третьей ил четвертой четверти. Запишите эту информацию в тетради со слайда (слайд 10) 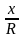 , то знак косинуса зависит то знака х. тогда в первой и четвертой четвертях х 0, а во второй и третьей четвертях x находится в первой или четвертой четверти, и косинус является меньше нуля, если угол находится во второй или третьей четверти. Запишите это в тетради со слайда.
, то знак косинуса зависит то знака х. тогда в первой и четвертой четвертях х 0, а во второй и третьей четвертях x находится в первой или четвертой четверти, и косинус является меньше нуля, если угол находится во второй или третьей четверти. Запишите это в тетради со слайда.









