План урока
Курс__, гр__
Дисциплина: Математика
Преподаватель:
Тема урока: Преобразование тригонометрических выражений.
Преобразование тригонометрических выражений – это упрощение выражений, которое выполняется с помощью тригонометрических формул.
Теоретический материал для самостоятельного изучения
- Преобразование тригонометрических выражений – это их упрощение, которое выполняется с помощью тригонометрических формул.
Вот некоторые правила, которые помогут нам преобразовывать тригонометрические выражения.
- Если в тригонометрических выражениях разные меры угла, то их следует привести к единой, применяя правила:
1) )
)
Например: 
2)
Например:  .
.
- Если синусы, косинусы, тангенсы и котангенсы содержат разные аргументы, (углы),стараемся привести к одному аргументу (углу).
Например, с помощью формул двойного аргумента(угла)  заменяем на
заменяем на  по формуле
по формуле  .
.
- Если в тригонометрическом выражении необходимо поменять синус на косинус, тангенс на котангенс, то применяем формулы приведения.
Например:  , так как
, так как  , синус меняется на косинус.
, синус меняется на косинус.
 , так как
, так как  , тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
, тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
- Если тригонометрические выражения содержат большое количество тригонометрических функций, то необходимо привести к минимальному количеству видов функций. Для этого используем формулы приведения, основное тригонометрическое тождество или другие формулы.
Например:
вычислить  .
.
Заметим, что  ,
,  ,
,  .
.
Тогда данное выражение примет вид:  ;
;
в скобках формула косинуса двойного угла, т.е.  , значит
, значит

- Если в тригонометрическом выражении нужно понизить степень входящих в него компонентов, применяем формулу понижения степени или формулу половинного аргумента. Только помните: степень понижается, аргумент удваивается.
 ,
, ,
,  ,
, 
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
Например: упростите выражение  .
.
Применяем формулу понижения степени для косинуса и получаем:
 .
.
Чтобы определить рациональность значения тригонометрического выражения, мы должны знать, что из всех углов, содержащих рациональное число, лишь углы вида  ;
;  ;
;  , где k целое число, имеют рациональный косинус.
, где k целое число, имеют рациональный косинус.
Например,  число рациональное, так как
число рациональное, так как  .
.
Углы вида  ;
;  ;
;  , где k целое число, имеют рациональный синус.
, где k целое число, имеют рациональный синус.
Углы вида  ;
;  , где k целое число, имеют рациональный тангенс.
, где k целое число, имеют рациональный тангенс.
Примеры и разбор решения заданий тренировочного модуля:
Рассмотрим примеры преобразований тригонометрических выражений.
Пример 1.Вычислите:  .
.
Заметим, что в знаменателе данной дроби у синусов разные углы  и
и  . Используем формулу приведения:
. Используем формулу приведения:  и тогда наше выражение примет вид:
и тогда наше выражение примет вид:  , в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
, в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
Пример 2. Найдите  , если
, если  .
.
Так как  , то разделив числитель и знаменатель данной дроби на
, то разделив числитель и знаменатель данной дроби на  . Получаем:
. Получаем:
 , сократим и заменим
, сократим и заменим  на
на .
.
 , по условию
, по условию  =3, подставим это число в наше выражение:
=3, подставим это число в наше выражение:  .
.
Самостоятельно.
- Доказать тождество:

- Упростить выражение:

Просмотр содержимого документа
«Тема урока: Преобразование тригонометрических выражений.»
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Преобразование тригонометрических выражений.
Преобразование тригонометрических выражений – это упрощение выражений, которое выполняется с помощью тригонометрических формул.
Теоретический материал для самостоятельного изучения
Преобразование тригонометрических выражений – это их упрощение, которое выполняется с помощью тригонометрических формул.
Вот некоторые правила, которые помогут нам преобразовывать тригонометрические выражения.
Если в тригонометрических выражениях разные меры угла, то их следует привести к единой, применяя правила:
1)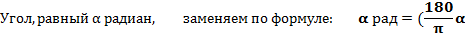 )
)
Например: 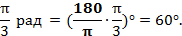
2)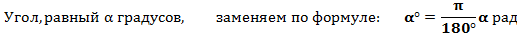
Например: 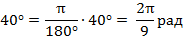 .
.
Если синусы, косинусы, тангенсы и котангенсы содержат разные аргументы, (углы),стараемся привести к одному аргументу (углу).
Например, с помощью формул двойного аргумента(угла) 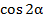 заменяем на
заменяем на  по формуле
по формуле 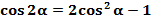 .
.
Если в тригонометрическом выражении необходимо поменять синус на косинус, тангенс на котангенс, то применяем формулы приведения.
Например: 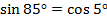 , так как
, так как 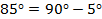 , синус меняется на косинус.
, синус меняется на косинус.
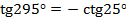 , так как
, так как 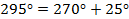 , тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
, тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
Если тригонометрические выражения содержат большое количество тригонометрических функций, то необходимо привести к минимальному количеству видов функций. Для этого используем формулы приведения, основное тригонометрическое тождество или другие формулы.
Например:
вычислить 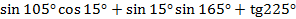 .
.
Заметим, что 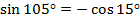 ,
, 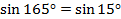 ,
, 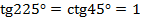 .
.
Тогда данное выражение примет вид: 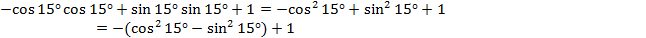 ;
;
в скобках формула косинуса двойного угла, т.е. 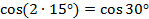 , значит
, значит
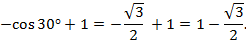
Если в тригонометрическом выражении нужно понизить степень входящих в него компонентов, применяем формулу понижения степени или формулу половинного аргумента. Только помните: степень понижается, аргумент удваивается.
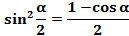 ,
,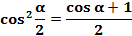 ,
, 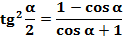 ,
, 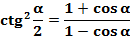
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
Например: упростите выражение 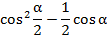 .
.
Применяем формулу понижения степени для косинуса и получаем:
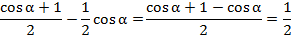 .
.
Чтобы определить рациональность значения тригонометрического выражения, мы должны знать, что из всех углов, содержащих рациональное число, лишь углы вида  ;
; 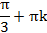 ;
; 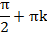 , где k целое число, имеют рациональный косинус.
, где k целое число, имеют рациональный косинус.
Например, 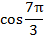 число рациональное, так как
число рациональное, так как 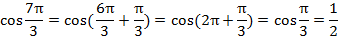 .
.
Углы вида 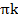 ;
; 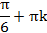 ;
; 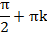 , где k целое число, имеют рациональный синус.
, где k целое число, имеют рациональный синус.
Углы вида 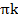 ;
; 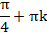 , где k целое число, имеют рациональный тангенс.
, где k целое число, имеют рациональный тангенс.
Примеры и разбор решения заданий тренировочного модуля:
Рассмотрим примеры преобразований тригонометрических выражений.
Пример 1.Вычислите: 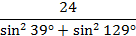 .
.
Заметим, что в знаменателе данной дроби у синусов разные углы 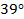 и
и 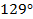 . Используем формулу приведения:
. Используем формулу приведения: 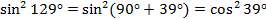 и тогда наше выражение примет вид:
и тогда наше выражение примет вид: 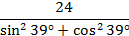 , в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
, в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
Пример 2. Найдите 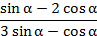 , если
, если 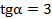 .
.
Так как 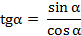 , то разделив числитель и знаменатель данной дроби на
, то разделив числитель и знаменатель данной дроби на  . Получаем:
. Получаем:
 , сократим и заменим
, сократим и заменим 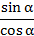 на
на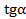 .
.
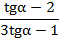 , по условию
, по условию 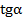 =3, подставим это число в наше выражение:
=3, подставим это число в наше выражение: 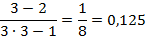 .
.
Самостоятельно.
Доказать тождество: 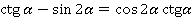
Упростить выражение: 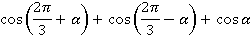






 )
)


 .
. заменяем на
заменяем на  по формуле
по формуле  .
. , так как
, так как  , синус меняется на косинус.
, синус меняется на косинус. , так как
, так как  , тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
, тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный. .
. ,
,  ,
,  .
. ;
; , значит
, значит
 ,
, ,
,  ,
, 
 .
. .
. ;
;  ;
;  , где k целое число, имеют рациональный косинус.
, где k целое число, имеют рациональный косинус. число рациональное, так как
число рациональное, так как  .
. ;
;  ;
;  , где k целое число, имеют рациональный синус.
, где k целое число, имеют рациональный синус. ;
;  , где k целое число, имеют рациональный тангенс.
, где k целое число, имеют рациональный тангенс. .
. и
и  . Используем формулу приведения:
. Используем формулу приведения:  и тогда наше выражение примет вид:
и тогда наше выражение примет вид:  , в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
, в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24. , если
, если  .
. , то разделив числитель и знаменатель данной дроби на
, то разделив числитель и знаменатель данной дроби на  . Получаем:
. Получаем: , сократим и заменим
, сократим и заменим  на
на .
. , по условию
, по условию  =3, подставим это число в наше выражение:
=3, подставим это число в наше выражение:  .
.

 , сократим и заменим
, сократим и заменим 









