СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 31.07.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

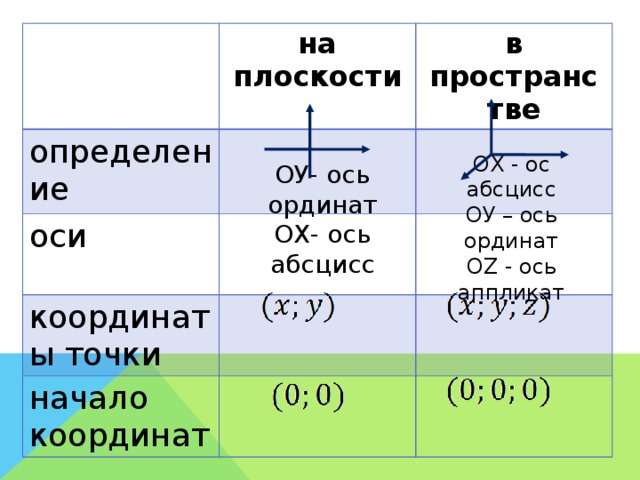
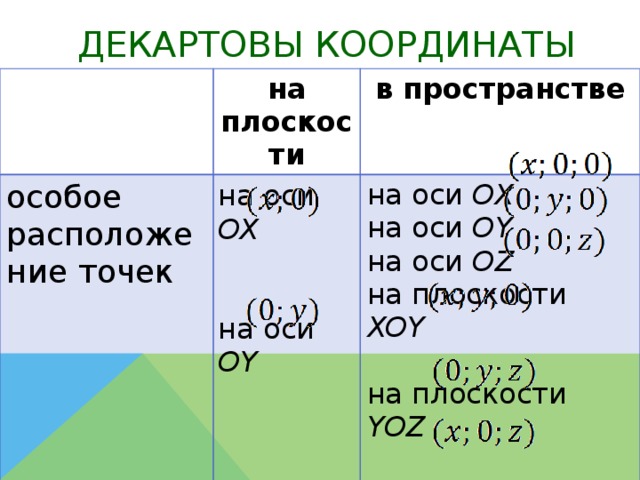
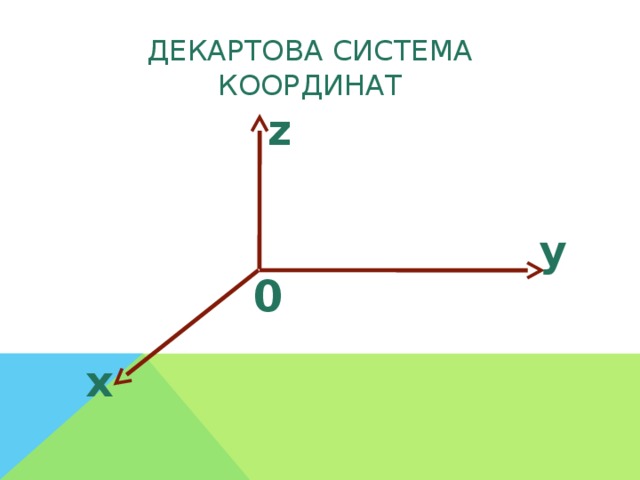
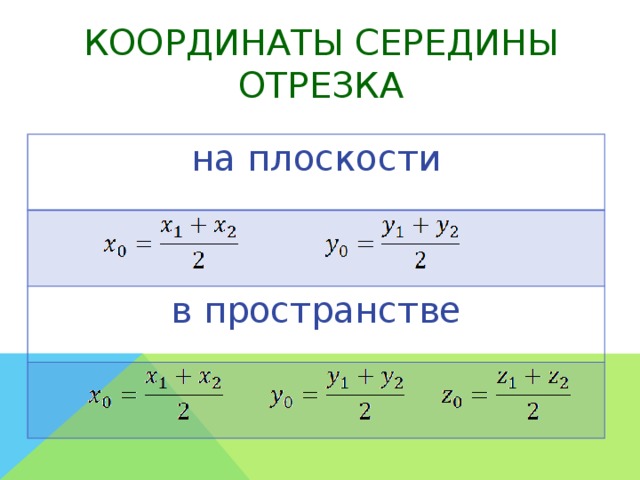
Система уроков по теме "Метод координат в пространстве"
Категория:
Математика
08.06.2018 11:19
Просмотр содержимого документа
«урок 1»
Просмотр содержимого документа
«урок 10 домашнее задание»
Просмотр содержимого документа
«урок 10 приложения»
Просмотр содержимого документа
«урок 10»
Просмотр содержимого документа
«урок 11 домашнее задание»
Просмотр содержимого документа
«урок 11»
Просмотр содержимого документа
«урок 12 контрольная работа»
Просмотр содержимого презентации
«урок 1»
Просмотр содержимого презентации
«урок 10»
Просмотр содержимого презентации
«урок 11»
© 2018, Кришталь Елена Николаевна 10980 743




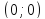
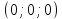
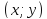
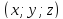
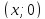
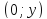
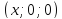
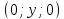
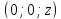
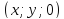
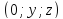
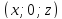
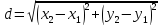
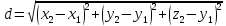
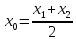
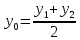
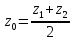
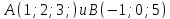
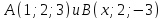
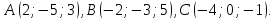
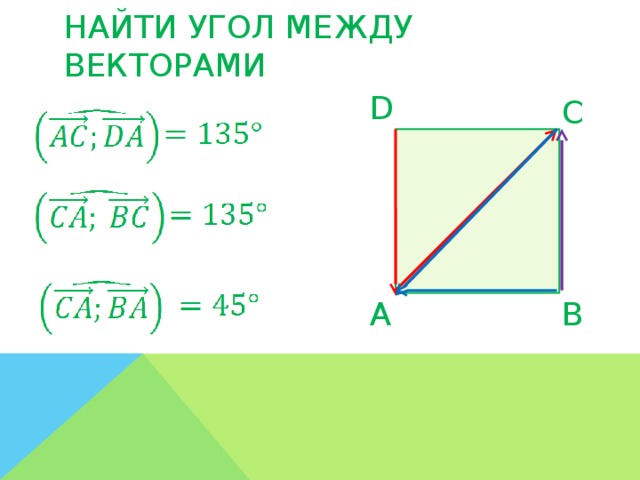
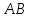 ;
;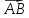 ;
;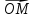 , где
, где 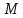 – середина отрезка
– середина отрезка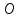 – начало координат;
– начало координат;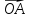 и
и 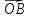 ;
;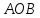 ;
;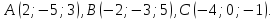
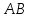 ;
;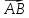 ;
;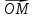 , где
, где 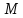 – середина отрезка
– середина отрезка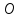 – начало координат;
– начало координат;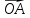 и
и 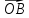 ;
;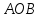 ;
;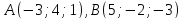 .
.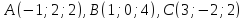 .
.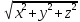
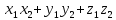
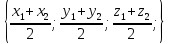
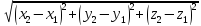
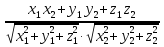
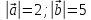 .
.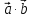 , если:
, если: 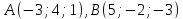 .
.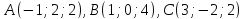 .
.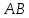 ;
;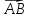 ;
;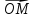 , где
, где 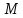 – середина отрезка
– середина отрезка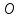 – начало координат;
– начало координат;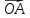 и
и 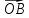 ;
;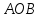 ;
;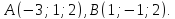
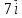
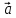 и
и 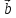 , если
, если 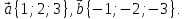
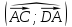 ,
, 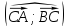 ,
, 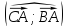
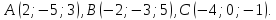
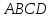 найдите угол между высотой тетраэдра
найдите угол между высотой тетраэдра 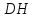 и медианой
и медианой 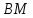 боковой грани
боковой грани 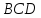 .
.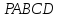 равны между собой. Найдите угол между прямыми
равны между собой. Найдите угол между прямыми 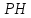 и
и 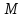 — середина ее бокового ребра
— середина ее бокового ребра 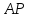 .
.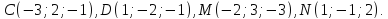
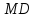
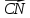 ;
;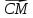 и
и 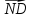 .
.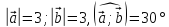 .
.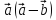 .
.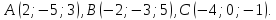
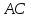 ;
;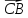 ;
;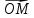 , где
, где 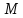 – середина отрезка
– середина отрезка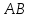 ,
, 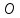 – начало координат;
– начало координат;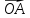 и
и 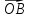 ;
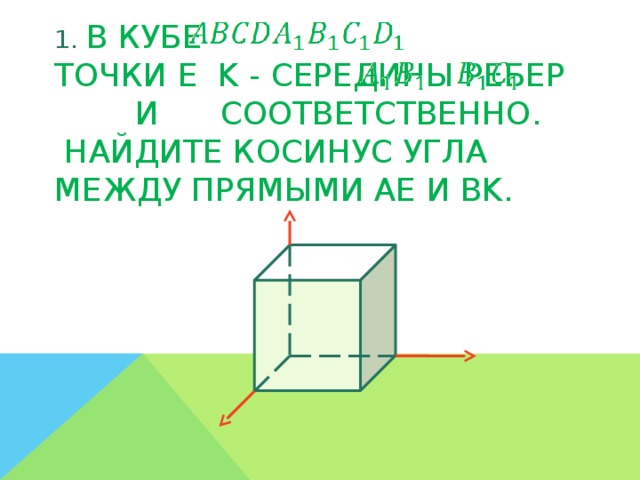
;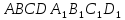 точки E и K - середины ребер
точки E и K - середины ребер 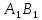 и
и 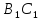 соответственно. Найдите косинус угла между прямыми AE и BK.
соответственно. Найдите косинус угла между прямыми AE и BK.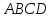 найдите угол между высотой тетраэдра
найдите угол между высотой тетраэдра 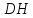 и медианой
и медианой 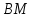 боковой грани
боковой грани 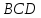 .
.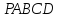 равны между собой. Найдите угол между прямыми
равны между собой. Найдите угол между прямыми 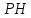 и
и 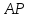 .
.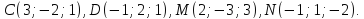 Найдите:
Найдите: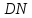
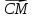 ;
;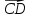 и
и 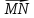 .
.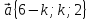 и
и 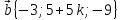 перпендикулярны?
перпендикулярны?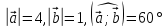 . Найдите значение выражения
. Найдите значение выражения 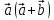
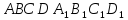 найдите угол между прямыми
найдите угол между прямыми 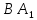 и
и 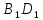 .
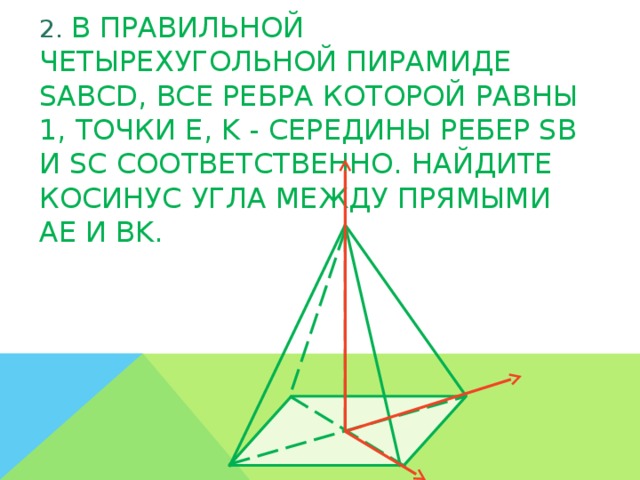
.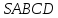 , все рёбра которой равны 1, точки К и Е – середины рёбер
, все рёбра которой равны 1, точки К и Е – середины рёбер 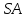 и
и 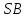 соответственно. Найти угол между прямыми
соответственно. Найти угол между прямыми 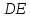
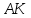
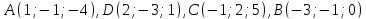 . Найдите:
. Найдите: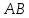
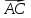 ;
;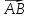 .
.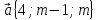 и
и 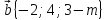 перпендикулярны?
перпендикулярны?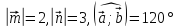 . Найдите значение выражения
. Найдите значение выражения 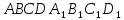 найдите угол между прямыми
найдите угол между прямыми 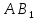 и
и 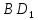 .
.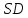 соответственно. Найти угол между прямыми
соответственно. Найти угол между прямыми 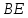 и
и