Системы счисления

СИСТЕМЫ СЧИСЛЕНИЯ

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ

Общие сведения

Система счисления - это знаковая система, в которой приняты определённые правила записи чисел.

Цифры - знаки, при помощи которых записываются числа.

Алфавит системы счисления - совокупность цифр.

Узловые и алгоритмические числа

Узловые числа обозначаются цифрами.

Алгоритмические числа получаются в результате каких-либо операций из узловых чисел.

 100 +

 10 +

=

Унарная система счисления

Простейшая и самая древняя система - унарная система счисления. В ней для записи любых чисел используется всего один символ - палочка, узелок, зарубка, камушек.

Узелковое письмо «кипу»

Непозиционная система счисления

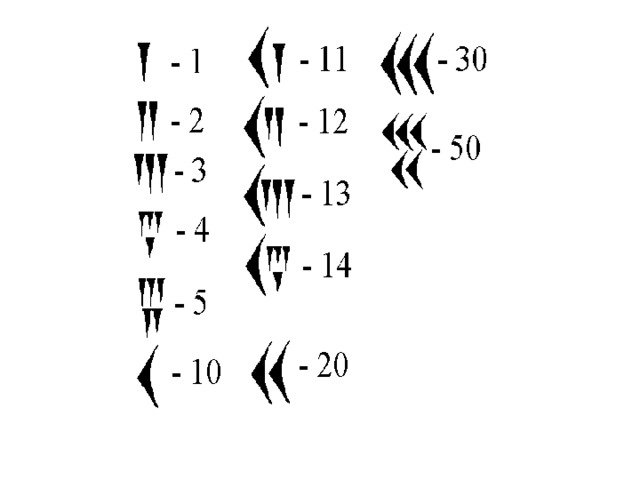
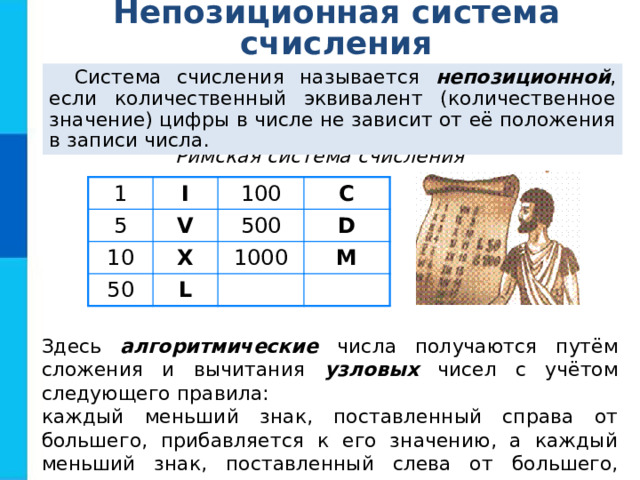
Система счисления называется непозиционной , если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.

Римская система счисления

1

I

5

V

10

100

X

50

500

C

D

L

1000

M

Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:

каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.

Позиционная система счисления

Система счисления называется позиционной , если количественный эквивалент цифры в числе зависит от её положения в записи числа.

Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

«Компьютерные» системы счисления

Двоичная система используется в компьютерной технике, так как:

• двоичные числа представляются в компьютере с помощью простых технических элементов с двумя устойчивыми состояниями;
• представление информации посредством только двух состояний надёжно и помехоустойчиво;
• двоичная арифметика наиболее проста;
• существует математический аппарат, обеспечивающий логические преобразования двоичных данных.

Двоичный код удобен для компьютера.

Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.

Двоичная система счисления

Двоичной системой счисления называется позиционная система счисления с основанием 2 .

Двоичный алфавит : 0 и 1.

10011 2

1110000 2

Восьмеричная система счисления

Восьмеричной системой счисления называется позиционная система счисления с основанием 8.

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.

1063 8

251 8

Десятичная система счисления

Десятичной системой счисления называется позиционная система счисления с основанием 8.

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

3891

173

Шестнадцатеричная система счисления

Основание : q = 16.

Алфавит : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

9А 16

3АF 16

Перевод чисел из 10-й СС в 2-ю СС

Правила перевода

• Разделить десятичное число на 2. Получится частное и остаток.
• Частное опять разделить на 2. Выполнять деление до тех пор, пока последнее частное не станет меньшим 2.
• Записать последнее частное и все остатки в обратном порядке. Полученное число и будет двоичной записью исходного десятичного числа.

Записываем выделенные остатки в обратном порядке

Перевод чисел из 10-й СС в 2-ю СС

57

57 10 → Х 2

2

28

56

2

28

2

14

1

14

0

7

2

6

3

2

0

2

1

1

1

Ответ:

57 10 = 111001 2

Записываем выделенные остатки в обратном порядке

Перевод чисел из 10-й СС в 8-ю СС

100 10 → Х 8

100

8

12

96

8

8

4

1

4

Ответ:

100 10 = 144 8

Записываем выделенные остатки в обратном порядке

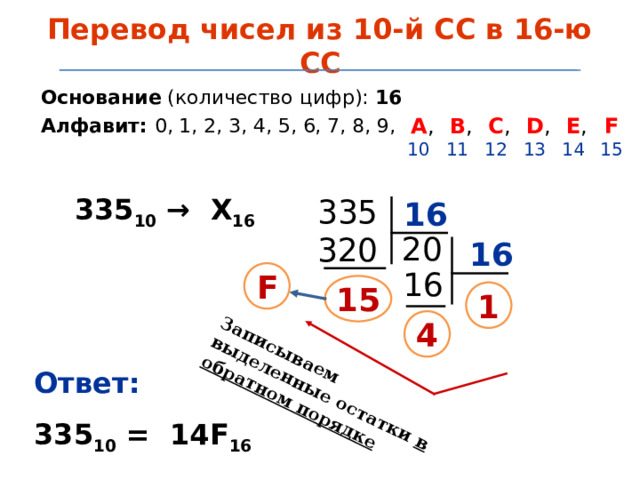
Перевод чисел из 10-й СС в 16-ю СС

Основание (количество цифр): 16

Алфавит: 0, 1 , 2 , 3, 4, 5, 6, 7, 8, 9,

D , 13

E , 14

C , 12

B , 11

A , 10

F 15

335 10 → Х 16

335

16

20

320

16

16

F

15

1

4

Ответ:

335 10 = 14 F 16

Перевод из 2-ой в 10-ую СС

Для перехода из двоичной системы счисления в десятичную необходимо двоичное число представить в виде суммы степеней двойки и найти ее десятичное значение.

Разряд цифры

3 2 1 0

+1* 2 2 +0* 2 1 +1* 2 =

1101 2

= 1* 2 3

=8+4+1 = 13

Основание системы

Перевод из 8-ой в 10-ую СС

1 0

71 8

= 7* 8 1 +1* 8 0 = 56+1= 57 10

2 1 0

144 8

= 1 · 8 2 + 4 · 8 1 + 4 · 8 0 =

= 64 + 32 + 4 = 100 10

Перевод из 16-ой в 10-ую СС

1 0

= 7 · 16 1 + 10 · 16 0 =

= 112 + 10 = 122 10

7А 16

2 1 0

= 2 · 16 2 + 12 · 16 1 + 6 · 16 0 =

= 512 + 192 + 6 = 710 10

2С6 16

2 1 0

1 C5 16

= 1 ·16 2 + 12 ·16 1 + 5·16 0

= 256 + 192 + 5 = 453