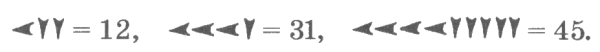Системы счисления

Цифры майя

Цифры майя — запись чисел, основанная на двадцатеричной^[1] позиционной системе счисления, использовавшаяся цивилизацией Майя в доколумбовой Месоамерике.

Цифры майя

Эта система использовалась для календарных расчётов. В быту майя использовали непозиционную систему, сходную с древнеегипетской^[2]. Об этой системе дают представление сами цифры майя, которые являются записью первых 19 натуральных чисел в пятеричной непозиционной системе счисления. Аналогичный принцип составных цифр использован в древнейшей известной шестидесятеричнойпозиционной системе счисления^[3].

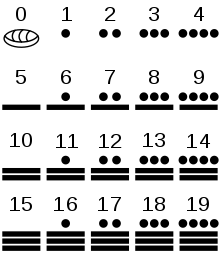
Цифры майя состояли из нуля, который обозначался пустой ракушкой, и 19 составных цифр. Эти цифры конструировались из знака единицы (точка) и знака пятёрки (горизонтальная черта). Например, цифра, обозначающая число 19, писалась как четыре точки в горизонтальном ряду над тремя горизонтальными линиями^[4].

Числа свыше 19

Общая формула записи чисел от двадцати включительно и выше, выглядит так:

[+ №3] [+ №2] [+ №1] , где

№3 - количество групп чисел по четыре сотни (если таковые имеются, иначе пропуск);

№2 - количество групп чисел по два десятка (если таковые имеются, иначе пропуск);

№1 - число (1..19).

Например:

• 32 писалось как (1)(12) = 1 × 20 + 12

• 429 как (1)(1)(9) = 1 × 400 + 1 × 20 + 9

• 4805 как (12)(0)(5) = 12 × 400 + 0 × 20 + 5

Для записи цифр от 1 до 19 иногда также использовались изображения божеств. Такие цифры использовались крайне редко, сохранившись лишь на нескольких монументальных стелах.

Третий разряд (четырёхсотки)
Второй разряд (двадцатки)
Первый разряд (единицы)
	32	429	4805

Ноль

Позиционная система счисления требует использования ноля для обозначения пустых разрядов. Первая дошедшая до нас дата с нолём (на стеле 2 в Чиапа-де Корсо, Чьяпас) датирована 36 годом до н. э. Изначально, первая в Евразии позиционная система счисления (созданная Вавилонянами за 2000 лет до нашей эры) была лишена ноля, но впоследствии всё-таки его приобрела. Использовался "0" (ноль) только в промежуточных разрядах числа, что приводило к многозначительной записи чисел. Другие системы счисления иных древних народов, как правило, были лишены ноля ^[2].

В календаре[править | править вики-текст]

Подробное изображение трёх колонок на стеле 1 в Ла-Мохарра. Левая дата — 8.5.16.9.7, то есть 156 год н. э.

В «долгом счёте» календаря майя применялась разновидность двадцатеричной системы счисления, в которой второй разряд мог содержать только цифры от 0 до 17, после чего к третьему разряду добавлялась единица. Таким образом, единица третьего разряда означала не 400, а 18 × 20 = 360, что близко к числу дней в солнечно

Вавилонская система счисления

Идея приписывать цифрам разные величины в зависимости от того, какую позицию они занимают в записи числа, впервые появилась в Древнем Вавилоне примерно в III тысячелетии до нашей эры.

До нашего времени дошли многие глиняные таблички Древнего Вавилона, на которых решены сложнейшие задачи, такие как вычисление корней, отыскание объема пирамиды и др. Для записи чисел вавилоняне использовали всего два знака: клин вертикальный (единицы) и клин горизонтальный (десятки). Все числа от 1 до 59 записывались с помощью этих знаков, как в обычной иероглифической системе.

Пример:

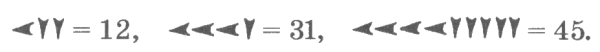
Все число в целом записывалось в позиционной системе счисления с основанием 60. Поясним это на примерах.

Запись 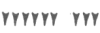 обозначала 6 • 60 + 3 = 363, подобно тому как наша запись 63 обозначает 6 • 10 + 3.

Запись  обозначала 32 • 60 + 52 = = 1972; запись  обозначала 1 • 60 • 60 + 2 • 60 + + 4 = 3724.

Был у вавилонян и знак, игравший роль нуля. Им обозначали отсутствие промежуточных разрядов. Но отсутствие младших разрядов не обозначалось никак. Так, число 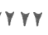 могло обозначать и 3, и 180 = 3 • 60 и 10 800 = 3 • 60 • 60 и так далее. Различать такие числа можно было только по смыслу.

Отголоски этой системы счисления мы находим в сохранившемся до наших дней обыкновении делить один час на 60 минут, одну минуту на 60 секунд, полный угол — на 360 градусов.

Шестидесятеричная система счисления

Шестидесятери́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 60. Изобретена шумерами в III тысячелетии до н. э., использовалась в древние времена на Ближнем Востоке.

Исторический очерк[править | править вики-текст]

Происхождение шестидесятеричной системы неясно. По одной гипотезе (И. Н. Веселовский), она связана с применением двенадцатеричной системы счисления и счёта на пальцах (60 = 5 × 12, где 5 — число пальцев на руке)^[1]. Существует также гипотеза О. Нейгебауэра (1927)^[2] о том, что после аккадского завоевания шумерского государства там долгое время одновременно существовали две денежно-весовые единицы: шекель (сикль) и мина, причём было установлено их соотношение 1 мина = 60 шекелей. Позднее это деление стало привычным и породило соответствующую систему записи любых чисел. И. Н. Веселовский выступил с критикой этой гипотезы, отметив, что шестидесятеричная система существовала у шумеров задолго до аккадского завоевания, ещё в IV тысячелетии до н. э.^[3] Другие историки оспаривают это утверждение Веселовского и на основании археологических находок доказывают, что исконная числовая система шумеров (в IV тысячелетии до н. э.) была десятичной^[4]. Французский историк Жорж Ифра^[en] в своей классической монографии «Всеобщая история чисел» (1985) аргументировал мнение, близкое к гипотезе Веселовского: шестидесятеричная система есть результат наложения двух более древних систем — двенадцатиричной и пятеричной. Археологические находки показали, что обе эти системы действительно реально использовались, а шумерские названия чисел 6, 7 и 9 обнаруживают следы пятеричного счёта, видимо, наиболее древнего^[5].

Вавилонское государство также унаследовало шестидесятеричную систему и передало её, вместе с таблицами наблюдений за небом, греческим астрономам. В более позднее время шестидесятеричная система использовалась арабами, а также древними и средневековыми астрономами, в первую очередь, для представления дробей. Поэтому средневековые учёные часто называли шестидесятеричные дроби «астрономическими». Эти дроби использовались для записи астрономических координат — углов, и эта традиция сохранилась по сей день. В одном градусе 60 минут и в одной минуте 60 секунд.

В XIII веке влиятельный ректор Парижского университета Пётр Филомен (он же Petrus de Dacia^[6]) выступил за повсеместное внедрение шестидесятеричной системы в Европе. В XV веке с аналогичным призывом выступил Иоганн Гмунден, профессор математики Венского университета. Обе инициативы остались без последствий.

Начиная с XVI века, десятичные дроби в Европе полностью вытесняют шестидесятеричные. Сейчас шестидесятеричную систему применяют при измерении углов и времени. Причём за пределами Европы, в КНР, шестидесятеричная система иногда используется не только для секунд и минут, но и для лет. Так, в пятом издании (2005 год) популярного в КНР словаря Сяньдай Ханьюй Цидянь^[en] приведена таблица правителей с указанием года как по десятичной системе, так и иероглифического обозначения номера года в шестидесятилетнем цикле^[7].

Структура шестидесятеричного числа[править | править вики-текст]

Первый шестидесятеричный знак после запятой называется минута (′), второй — секунда (″). Ранее использовались названия терция (‴) для третьего знака, кварта (^IV) для четвёртого знака, квинта (^V) для пятого знака и т. д. Название «минута» происходит от того же слова, что и «минимум» — обозначает «малая часть», а «секунда», «терция» и остальные являются порядковыми — «второе» деление на части, «третье» деление на части и т. п.Частей традиционно берётся по 60.

Примеры использования[править | править вики-текст]

• 1 радиан ≈ 57°17′45″ = {\displaystyle \left(57+{\frac {17}{60}}+{\frac {45}{60^{2}}}\right)^{\circ }}.

• Николай Коперник в знаменитой работе «О вращениях небесных сфер» даёт значение сидерического года 365;15′24″10‴ дней, приблизительно 365,25671 дней.

Вавилонская система счисления[править | править вики-текст]

Вавилонская система счисления применялась за две тысячи лет до н. э. Для записи чисел использовались всего два знака: стоячий клин  для обозначения единиц и лежачий клин 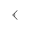 для обозначения десятков внутри шестидесятеричного разряда.

Таким образом, вавилонские цифры были составными и записывались как числа в десятеричной не позиционной системе счисления. Аналогичный принцип использовали индейцы Майя в своей двадцатеричной позиционной системе счисления. Для понимания записи числа между вавилонскими цифрами необходимы «пробелы».

 = 62,  = 122 и  = 129.

Система использовалась для записи, как целых, так и дробных чисел.

Вавилонская табличка с числом 1;24,51,10 — наиболее точным приближением квадратного корня из двухчетырьмя шестидесятеричными цифрами

Вначале нуля не было, что приводило к неоднозначной записи чисел, и об их значении приходилось догадываться по контексту. Позже (между VI и III веком до нашей эры) появилось обозначение «нуля» , но только для обозначения пустых шестидесятеричных разрядов в середине числа^[8][9]. Заключительные нули числа не писались, и запись чисел оставалась неоднозначной.

Двенадцатеричная система счисления

[

МДвенадцатеричная система счисления — позиционная система счисления с основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Существует другая система обозначения, где для недостающих цифр используют не A и B, а T (от англ. ten, десять) или D (от лат. decem, фр. dix, десять) или X (римское десять), а также E (от англ. eleven, одиннадцать) или O (от фр. onze, одиннадцать). Кроме того, на Западе иногда вместо A используют перевёрнутую двойку (, U+218A ↊turned digit two) и вместо B перевёрнутую тройку ( , U+218B ↋ turned digit three).

Число 12 могло бы быть очень удобным основанием системы счисления, так как оно делится нацело на 2, 3, 4 и 6, в то время как число 10 — основание десятичной системы счисления — делится нацело лишь на 2 и 5.

Двенадцатеричная система счисления возникла в древнем Шумере. Предполагается, что такая система возникала, исходя из количества фаланг четырёх пальцев руки (исключая большой) при подсчёте их большим пальцем той же руки.^[1][2][3]Фаланги пальцев использовались как простейшие счёты (текущее состояние счёта засекалось большим пальцем), вместо загибания пальцев, принятого в европейской цивилизации. Некоторые народы Нигерии и Тибета используют двенадцатеричную систему счисления в настоящее время.

Также существует гипотеза, что до 12 считали сидя, загибая не только 10 пальцев рук, но и 2 ноги. Хотя, возможно, такое случалось, когда европейцам приходилось сталкиваться с восточным двенадцатеричным счётом.

Двенадцатые доли часто встречались и в европейских системах мер. У римлян стандартной дробью была унция (1/12). 1 английский пенни (пенс) = ¹⁄₁₂ шиллинга, 1 дюйм = ¹⁄₁₂ фута и т. д.

Переход на двенадцатеричную систему счисления предлагался неоднократно. В XVII веке её сторонником был знаменитый французский естествоиспытатель Бюффон. Вольтер в «Истории Карла XII» утверждает, что этот монарх готовил указ о переходе на двенадцатеричную систему.^[4] Во времена Великой французской революции была учреждена «Революционная комиссия по весам и мерам», которая длительный период рассматривала подобный проект, однако усилиями Лагранжа и других противников реформы дело удалось свернуть. В 1944 году было организовано «Американское двенадцатеричное общество» (англ. The Dozenal Society of America (DSA)), а в 1959 — «Английское двенадцатеричное общество» (англ. The Dozenal Society of Great Britain (DSGB)), объединившие активных сторонников одноимённой системы счисления. Однако главным аргументом против этого всегда служили огромные затраты и неизбежная путаница при переходе. ^{[источник не указан 701 день]}

Двенадцатеричный счёт[править | править вики-текст]

«Счёт дюжинами»

Элементом двенадцатеричной системы в современности может служить счёт дюжинами. Первые три степени числа 12 имеют собственные названия:

• 1 дюжина = 12 штук

• 1 гросс = 12 дюжин = 144 штуки

• 1 масса = 12 гроссов = 1728 штук

К удобствам двенадцатеричного счисления можно отнести большее (по сравнению с десятичной системой) количество делителей основания 12 - 2, 3, 4, 6. На практике двенадцатеричная система (в смешанном виде) осталась в часах.

Кириллическая система счисления

[

Башенные часы с кириллическими цифрами в Суздале

Кирилли́ческая систе́ма счисле́ния — система счисления Древней Руси, основанная на алфавитной записи чисел с использованием кириллицы или глаголицы.

В основных чертах схожа с греческой системой счисления.

Использовалась в России до начала XVIII века, когда была заменена на систему счисления, основанную на арабских цифрах.

В настоящее время используется в книгах на церковнославянском языке.

Единицы, десятки и сотни

Примеры записи чисел кириллицей

Большинство букв древнерусского алфавита имели числовое соответствие. Так, буква «Аз» означала «один», «Веди» — «два»… Некоторые буквы числовых соответствий не имели. Числа писались и произносились слева направо, за исключением чисел от 11 до 19 (например, 17 — сем-на-дцать).

По такому же принципу строилась глаголическая система счисления, в которой использовались буквы глаголицы.

В начале XVIII века иногда применялась смешанная система записи чисел, состоящая и из кириллических, и из арабских цифр. Например, на некоторых медных полушках (монетах достоинством ¼ копейки) отчеканена дата 17К (1720) и 17К1 (1721).

Таблица соответствия букв числам[

Кириллическая система счисления почти буква в букву воспроизводит греческую. В глаголице цифровые значения имеют и те буквы, которые отсутствуют в греческом (буки, живете и др.). В церковнославянском варианте, используемом и сегодня, она имеет следующий вид:

Число	Греческий алфавит	Кириллица		Глаголица
1	Α, α	А (аз)		А (аз)
2	Β, β	В (веди)		Б (буки)
3	Γ, γ	Г (глаголь)		В (веди)
4	Δ, δ	Д (добро)		Г (глаголь)
5	Ε, ε	Е (есть)		Д (добро)
6	Ϛ, ϛ (стигма)	S (зело)		Е (есть)
7	Ζ, ζ	З (земля)		Ж (живете)
8	Η, η	И (иже)		S (зело)
9	Θ, θ	Ѳ (фита)		З (земля)
10	Ι, ι	I (и)		I (и)
20	Κ, κ	К (како)		И (иже)
30	Λ, λ	Л (люди)		Ћ (гервь)
40	Μ, μ	М (мыслете)		К (како)
50	Ν, ν	Н (наш)		Л (люди)
60	Ξ, ξ	Ѯ (кси)		М (мыслете)
70	Ο, ο	О (он)		Н (наш)
80	Π, π	П (покой)		О (он)
90	Ϟϟ (коппа)	Ч (червь)		П (покой)
100	Ρ, ρ	Р (рцы)		Р (рцы)
200	Σ, ς	С (слово)		С (слово)
300	Τ, τ	Т (твердо)		Т (твердо)
400	Ο, ο и Υ, υ	У (ук)		У (ук)
500	Φ, φ	Ф (ферт)		Ф (ферт)
600	Χ, χ	Х (хер)		Х (хер)
700	Ψ, ψ	Ѱ (пси)		Ѡ (от)
800	Ω, ω	Ѡ (омега)		Щ (шта)
900	Ϡϡ (сампи)	Ц (цы)		Ц (цы)
1000	—	҂а		Ч (червь)

Особенности кириллической системы счисления[править | править вики-текст]

Основная статья: Алфавитная запись чисел

Для записи чисел использовались почти исключительно строчные буквы.

Числовое значение 5 первоначально несла обычная буква е, так называемая узкая е, но так как по церковно-славянской орфографии она не могла стоять в начале слова или изолированно, позже стал применяться её другой вариант є, так называемая широкая е, из которого впоследствии развилась украинская буква «є».

Для числового значения 6 в древности применялась как обычная буква «зело» (ѕ), так и зеркально перевернутая.

Буква «і» в числовом употреблении точек не имеет.

По той же причине, что и для 5, для числового значения 70 обычно применяется не обычная буква «о», а её так называемый «широкий» вариант ѻ (в Юникоде по недоразумению названный «круглой омегой», англ. round omega).

Значение 90 в самых древних кириллических текстах выражала не буква «ч», а заимствованный из греческого знак «коппа» (ҁ).

Значение 400 в древности выражала буква «ижица (ѵ)», позже так называемый «ик» — у-образный знак, используемый только как числовой и в составе диграфа «ук» («оу»). Использование в числовом значении «ика» характерно для российских изданий, а «ижицы» — для старопечатных украинских, позднейших южнославянских и румынских.

В значении 800 могла применяться как «голая омега (ѡ)», так и (чаще) составной знак «от (ѿ)»; подробнее см. статью «Омега (кириллица)».

Значение 900 в древности выражалось «малым юсом» (ѧ), несколько похожим на соответствующую греческую букву «сампи» (Ϡ); позже в этом значении стала применяться буква «ц».

Титло[править | править вики-текст]

Примеры записи денежных сумм без титла (Акт передела меди в монету начала XVIII века)

Основная статья: Титло

Чтобы отличать буквы от цифр, над буквами с числовым значением писался специальный знак — титло. Этот знак мог ставиться над каждой буквой, либо же он мог быть длинным и покрывать всё число.

В первой печатной библии (XVI век) в двузначных и многозначных числах титло ставился над второй буквой от начала.

С XIX века в книгопечатании сложилась традиция в двузначных и многозначных числах титло ставить над второй буквой от конца.^[1]

В случае с денежными суммами титло иногда заменяли надстрочной лигатурой «ру», «де» или буквой «а», соответственно символами рубля, денги или алтына.

Тысячи[править | править вики-текст]

Для обозначения тысяч слева от соответствующей букво-цифры писалась маленькая диагональ влево вниз и на ней две маленькие черточки — ҂ (U+0482).

Примеры:

•  — 1706 год;

•  — 7118 год по летосчислению «от сотворения мира» (1610 год от Рождества Христова).

Десятки и сотни тысяч, миллионы[править | править вики-текст]

В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 19 августа 2017 года.

Большие числа (десятки и сотни тысяч, миллионы и миллиарды) могли выражаться не через знак «҂», а специальным образом обведенной буквой, использовавшейся для обозначения единиц. Впрочем, для больших чисел эти обозначения были довольно нестабильны.

 Тьма[править | править вики-текст]

Для обозначения тьмы буква обводилась сплошной окружностью.

• Малый счёт — десять тысяч ({\displaystyle 10^{4}}) или сто тысяч^{[источник не указан 747 дней]} ({\displaystyle 10^{5}});

• Великий счёт — тысяча тысяч, миллион ({\displaystyle 10^{6}}, тьма великая).

От слова тьма произошло воинское звание темник — крупный военачальник. Темником был, например, Мамай.

Аналогичными наименованиями являются тумэн, от которого, вероятно, и произошло слово тьма как название числа, и мириада (др.-греч. μῡριάς, μῡριάδος).

 Легион (неведий) или Легеон (несвѣдь)[править | править вики-текст]

См. также: Имя мне — легион

Для обозначения легиона (неведия) буква обводилась в кружок из точек или число записывалось следующим образом:

.

• Малый счёт — десять тем, или сто тысяч ({\displaystyle 10^{5}});

• Великий счёт — тьма тем, или триллион ({\displaystyle 10^{12}}).

 Лео́др[править | править вики-текст]

Для обозначения леодра буква обводилась в кружок из черточек или запятых, или записывалась третьим способом:

или записывалась четвёртым способом: 

• Малый счёт — десять легионов, или миллион ({\displaystyle 10^{6}});

• Великий счёт — легион легионов, или септиллион ({\displaystyle 10^{24}}).

 Вран (ворон)[править | править вики-текст]

Для обозначения врана (ворона) буква обводилась в кружок из крестиков; или справа и слева от буква ставили буквы к, а над буквой буквой изображали титло;

• Малый счёт — десять леодров, или десять миллионов ({\displaystyle 10^{7}});

• Великий счёт — леодр леодров, или квиндециллион ({\displaystyle 10^{48}}).

 Клада (колода)[править | править вики-текст]

Буква заключалась в квадратные или круглые скобки, но не справа и слева, как у обычных букв, а сверху и снизу.

• Малый счёт — десять вранов, или сто миллионов ({\displaystyle 10^{8}});

• Великий счёт — десять вранов, или 10 квиндециллионов ({\displaystyle 10^{49}}).

 Тьма тем[править | править вики-текст]

Самое большое число — тьма тем.

• Малый счёт — десять колод, или миллиард ({\displaystyle 10^{9}});^[2][3][4]

• Великий счёт — десять колод, или 100 квиндециллионов ({\displaystyle 10^{50}}, тьма великая).^{[источник не указан 752 дня]}

В малом счёте число служило последним пределом естественного (соотносимого с какой-либо деятельностью) счёта. Тьма тьмущая — бесконечное количество, неисчислимое множество.