Сочетания и число сочетаний

Элементы комбинаторики

9 класс

Оригинальные шаблоны для презентаций: https://presentation-creation.ru/powerpoint-templates.html

Бесплатно и без регистрации.

• Подготовила: учитель математики МБОУ СОШ №108
• Шестеренникова Ксения Евгеньевна

Г. Новосибиск, 2023

Проверка домашнего задания

2 730

210

303 600

Устно

В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по-английски, трое только по-французски, двое по-французски

и по-английски. Какова вероятность того, что случайно выбранный турист говорит по-французски?

Устно

В коробке 14 пакетиков с черным чаем и 6 пакетиков с зеленым чаем. Павел наугад вынимает один пакетик. Какова вероятность того, что это пакетик с зеленым чаем?

• Сколько трехзначных чисел можно составить из цифр 1, 3, 5 и 7, используя в записи числа каждую из них не более одного раза?
• 24
• Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета.
• 1 680
• Имеется пять роз разного цвета: белая, желтая, оранжевая, розовая, красная. Какие букеты из 3-х роз могут быть составлены?
• 10

Рассмотрим пример

ПРИМЕР. Пусть имеется пять роз разного цвета:

Б – белая, Ж – желтая, 0 – оранжевая, Р – розовая, К – красная.

Какие букеты из 3-х роз могут быть составлены?

Решение.

Составим букеты 1-м способом (т.е. перебором).

Если в букете обязательно будет белая роза, то могут быть составлены следующие букеты:

БЖО, БЖР, БЖК, БОР, БОК, БРК (6 вариантов).

Если в букете не будет белой, но обязательно будет желтая роза, то могут быть составлены следующие букеты:

ЖОР, ЖОК, ЖРК (3 варианта).

№ 714 Макарычев 9 кл

Если в букете не будет ни белой, ни желтой розы, то может быть составлен только один букет:

ОРК (1 вариант).

Итого: 10 вариантов.

Рассмотрим пример

Мы указали все возможные варианты составления букетов, в которых по-разному сочетаются три розы из данных пяти. Говорят, что мы составили все возможные сочетания из 5 элементов по 3.

В чем отличие от размещений?

В отличие от размещений в сочетаниях не имеет значения, в каком порядке указаны элементы. Любые два сочетания из n элементов по k отличаются друг от друга хотя бы одним элементом.

Сочетания

• Сочетанием из n элементов по k (k n) называется любое множество, состоящее из k элементов, выбранных из данных n элементов.

• Сочетания бывают без повторения элементов и с повторениями .
• Число сочетаний из n элементов по k без повторений обозначают (читается: «C из n по k», от франц. combination - сочетание).

В рассмотренной выше задаче = 10 .

Формула числа сочетаний (без повторений)

Рассмотрим общий случай.

Пусть имеется множество, состоящее из n элементов, из которых составлены все возможные сочетания по k элементов. Число таких сочетаний равно .

=

Решаем в парах

В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

Решение.

Так как порядок, в котором будут выбраны два человека, на важен, то число различных способов вычисляется по формуле для числа сочетаний:

= = = = 21

Решаем в парах

Задача. В классе учатся 12 мальчиков и 10 девочек. Для уборки территории около школы требуется выделить трех мальчиков и двух девочек. Сколькими способами это можно сделать?

Решение.

Выбрать трех мальчиков из 12 можно

способами.

Выбрать двух девочек из 10 можно

способами.

Так как при каждом выборе мальчиков можно способами выбрать девочек, то сделать выбор учащихся, о котором говорится в задаче, можно

способами:

= = = = 11 · 10 · 10 · 9 = 9900

Распредели верно

Перестановки

Перестановки

Размещения

Размещения

Сочетания

P n

Правило умножения (например 8*7*6*5)

Сочетания

P n

Правило умножения (например 8*7*6*5)

n!

n!

Самостоятельно. Распредели по группам и реши задачи

• На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места 4 фотографии?
• Сколько трехзначных чисел можно составить из цифр 1, 3, 5 и 7, используя в записи числа каждую из них не более одного раза?
• Имеются 9 различных книг. Сколькими способами можно расставить книги на 4х полках?
• Сколько существует способов выбрать троих ребят из четверых желающих дежурить по столовой?
• Сколькими способами 4 человека могут разместиться на четырехместной скамейке?
• В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

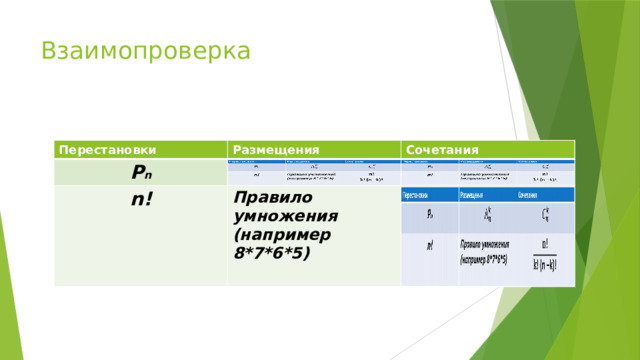
Взаимопроверка

Перестановки

Перестановки

Размещения

Размещения

P n

P n

Сочетания

n!

Сочетания

n!

Правило умножения (например 8*7*6*5)

Правило умножения (например 8*7*6*5)

Взаимопроверка с объяснением

Перестановки

Размещения

Сколько трехзначных чисел можно составить из цифр 1, 3, 5 и 7, используя в записи числа каждую из них не более одного раза?

Сочетания

На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места 4 фотографии?

Сколькими способами 4 человека могут разместиться на четырехместной скамейке?

Имеются 9 различных книг. Сколькими способами можно расставить книги на 4х полках?

Сколько существует способов выбрать троих ребят из четверых желающих дежурить по столовой?

В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

• 24
• 24

• 360
• 3 024

• 4
• 56

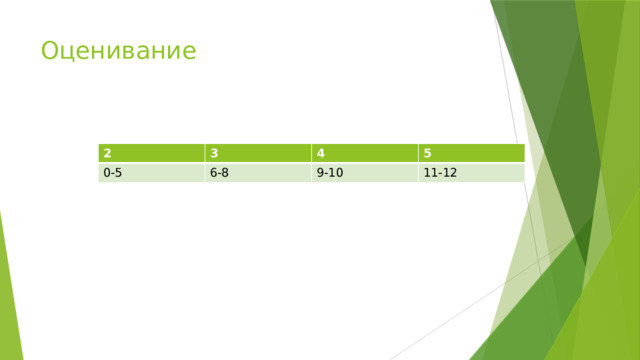
Оценивание

2

3

0-5

6-8

4

5

9-10

11-12

Рефлексия

Сегодня я повторил(а)….

Сегодня я узнал(а)….

Теперь я могу….

Мне было легко…

Сложнее всего было…