Создание проблемных ситуаций на уроках математики в средней школе

Создание проблемных ситуаций на уроках математики

Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей

Уровни проблемного обучения :

1 уровень – ученик усваивает приёмы логического мышления

репродуктивным методом, следуя образцу рассуждения учителя

;

2 уровень – учитель создаёт проблемную ситуацию, указывает на проблему и вовлекает их в совместный поиск путей её решения и в процесс самого решения;

3 уровень – учащиеся формулируют аналоговую неполнозначную проблему и анализируют её вместе с учителем, совместно выдвигают предположения и обосновывают гипотезу, а доказывают и проверяют решения самостоятельно, решаются познавательные задачи;

4 уровень – наличие любых типов проблем и полная

самостоятельность в их решении.

Технология проблемного обучения реализуется на основе следующих факторов:

• оптимальный подбор проблемных ситуаций и средств их создания;

• отбор ситуаций тесно связан с применением их в повседневной жизни;

• учет особенностей проблемных ситуаций в различных видах учебной работы и в различных классах;

• личностный подход и мастерство учителя, способные вызвать активную познавательную деятельность ребенка

Проблемное обучение, в первую очередь, включает в себя создание

проблемных ситуаций

Создание проблемных ситуаций через умышленно допущенные учителем ошибки

Решаются

• задачи с несформулированным вопросом
• с недостаточными или избыточными исходными данными;
• с неопределенностью в постановке вопроса;
• с противоречивыми данными;
• с заведомо допущенными ошибками;
• с ограниченным временем решения.

«Обманные задачи»

• Больший угол треугольника равен 50°. Найдите остальные углы.
• Две стороны треугольника перпендикулярны третьей. Определите вид треугольника.
• Внешний угол при основании равнобедренного треугольника равен 75°. Найдите углы треугольника.
• Диагональ ромба в два раза больше его стороны. Найдите углы ромба.

«Обманные задачи»:

7 кл. Тема «Линейные уравнения с одной переменной».

Проверьте решение уравнения:

(5х+ 8)  2 – 3 = 19

10х + 16 – 3 = 19

10х = 19 – 16 – 3

10х = 0

х = 0

Естественно при проверке выясняется, что ответ неверный.

Создание проблемных ситуаций через выполнение практических заданий

7 класс. Темы: «Построение треугольника по трем элементам», «Неравенство треугольника». Предлагаю ученикам построить с помощью циркуля и линейки треугольник со сторонами:

а) 5см; 6см; 7см; б) 9см; 5см; 6см;

в) 1см; 2см; 3см; г) 3см; 4см; 10см. Вывод: построить треугольник в последних двух случаях не удается.

Возникает проблема : «При каких же условиях можно построить треугольник, т. е. каково условие существования треугольника»? Чертежи, полученные учащимися при решении этой задачи дают возможность легко сделать вывод: «Каждая сторона треугольника меньше суммы двух других сторон».

Создание проблемных ситуаций через решение задач на сравнение и внимание

8кл. Тема «Осевая и центральная симметрия».

а) Какие из следующих букв имеют центр симметрии: А, О, М, Х, К ?

б) Какие из следующих букв имеют ось симметрии : А, Б, Г, Е, О, F?

Создание проблемных ситуаций через решение задач на сравнение и внимание

Задачи на внимание 5-8 классы

У Гарри Поттера есть волшебные очки, в которых он видит все зеленое - белым, а все белое - зеленым.

Гарри посмотрел через эти очки на прямоугольник, изображенный справа.

Что он увидел?

Создание проблемных ситуаций через противоречие нового материала старому, уже известному

7 кл. Тема «Формулы сокращённого умножения»

Вычисляем:

(2  5)²= 2²  5² = 100

(5 : 6)² = 5² : 6² = 25 : 36

(3 + 4)² = 3² + 4² = 9 + 16 = 25

Попробуйте сосчитать по-другому.

( 3 + 4)² =7² = 49

Проблемная ситуация создана .

Почему разные результаты? ( 3 +4)² ≠ 3² + 4²

Создание проблемных ситуаций через выполнение небольших исследовательских заданий

5кл. Тема «Длина окружности».

Ещё древние греки находили длину окружности по формуле C = *d.

d – диаметр окружности. Вопрос : что же такое ?

1. Опоясать стакан ниткой, распрямить нитку, длина нитки примерно

равна длине окружности стакана. Чтобы получить более точный

результат, нужно это проделать несколько раз.

Занесите данные в следующую таблицу:

2. Измерьте диаметр стакана линейкой. Данные занесите в табл.

3. Найдите значение , как неизвестного множителя.

Исследование проведено. Проблема решена.

С1

С2

С3

С сред.

Д

Создание проблемных ситуаций через использование занимательных задани й

7 кл. Тема: «Формулы сокращённого умножения»

Преступники украли в банке большую сумму денег. Их поймали, но похищенную сумму установить не удалось. Преступники категорически отказываются назвать её, утверждая, что записали это число в виде степени и зашифровали не только основание, но и её показатель. Экспертам удалось узнать основание степени. Это число 597. Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения

( 2y +1) 2 – 4y 2 =9

y = 2

597 2 = (600 – 3) 2 =600 2 -2 х 600 х 3 + 3 2 = 360000 – 3600 + 9 =356409

Создание проблемных ситуаций через решение задач , связанных с жизнью

8кл. Тема «Площадь прямоугольника».

Родители решили поменять входную дверь и заказали в фирме изготовить металлическую дверь. Им предоставили платёжный документ, в правильности которого папа усомнился, а именно в стоимости покраски двери. Попросил своего сына самому рассчитать стоимость данной работы.

Проблемная ситуация : нужно знать площадь двери (площадь прямоугольника) . Причём норма краски на 1 кв.м и стоимость работы покраски 1кв.м даны в документе.

Задача арабского математика XI в

На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?

Создание проблемных ситуаций через использование занимательных заданий

• . 9 кл. Тема «Сумма n-первых членов арифметической прогрессии»

Изучение вопроса о сумме n–первых членах арифметической прогрессии в 9-ом классе начинаю с рассказа: “Примерно 200 лет тому назад в одной из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ. Имя этого ученика Карл Фридрих Гаусс. В последствии он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму?”

Проблемная ситуация: как найти быстро сумму первых 100 натуральных чисел?

Решение проблемы (1 + 100)  50 = 5050

Последовательность чисел 1, 2, 3,…,100 является арифметической прогрессией. Теперь выводим формулу суммы n-первых членов арифметической прогрессии.

Создание проблемных ситуаций через различные способы решения одной задачи

Пример№1.8кл.Тема:«Квадратные уравнения»

Решить уравнение 3х 2 + 2х – 1 = 0 , используя различные способы.

1 способ . По общей формуле . D = b 2 – 4ac; D = 4 + 12 = 16 = 4 2. . Ответ: -1; 1/3. 2способ. По формуле с чётным коэффициентом b . D 1 = ( b/ 2) 2 – ac; D 1 = 1 + 3 = 4 = 2 2. Ответ: -1; 1/3. 3 способ. По теореме Виета

4 способ . Из условия , если а + с = b, то х 1 = - 1; х 2 = - с / а

5 способ . Выделение полного квадрата.

6 способ . Разложение на множители способом группировки 7 способ . Графический.

8 способ . Приведение к виду ( f( x) ) 2 = ( g(x) ) 2 .

Определение степени с

рациональным показателем.

(= = - = -2

(=( == = 2

Проблема: почему разные ответы.

Подсказка №1.

= 3∙

Решите систему уравнений:

Подсказка №2.

Умножить первое

уравнение на (-2)

и сложить

со вторым

Подсказка №3.

Выразить из первого

уравнения

или и подставить

во второе уравнение

Подсказка №4

Заменить дроби

и другими

буквами

Найдите ошибки в решении системы уравнений.

Ответ:(-1,25; - 3).

+

∙ (-2 )

11y = -33

y = -3

Найти соответствие между системой

уравнений и парой чисел, которая является её решением

Нажмите на клавишу изображением ладони

При правильно выбранном соответствии пара клавиш окрашивается в одинаковый цвет.

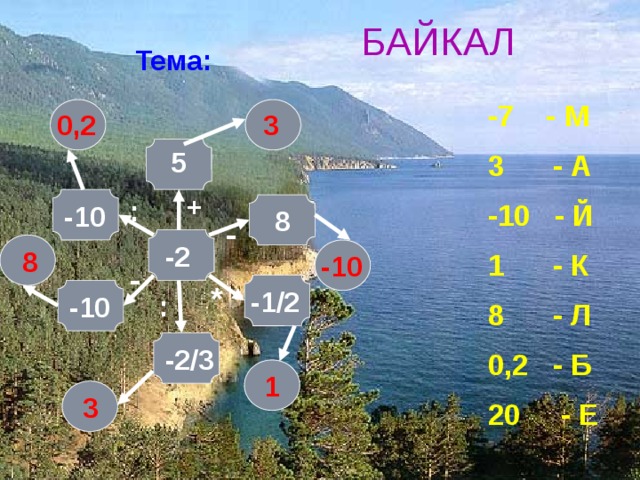
БАЙКАЛ

Тема:

-7 - М

3 - А

-10 - Й

1 - К

8 - Л

0,2 - Б

20 - Е

3

0,2

5

+

:

-10

8

-

-2

8

-10

-

*

-1/2

:

-10

-2/3

1

3

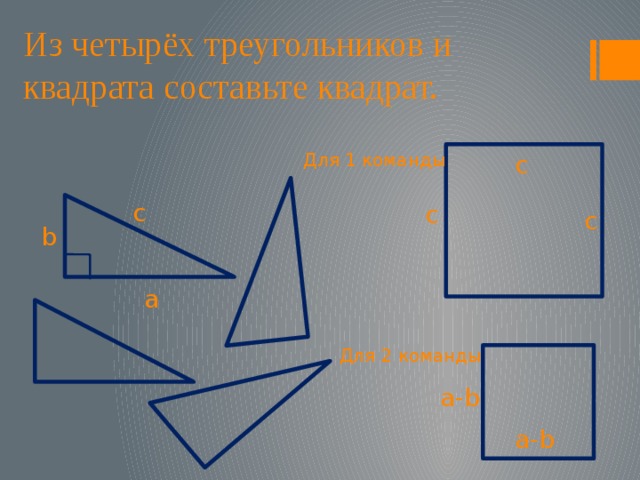
Из четырёх треугольников и квадрата составьте квадрат.

Для 1 команды

c

c

c

c

b

a

Для 2 команды

а-b

а-b

a

b

a + b

b

c

a

c

a

c

c

b

b

a

c

a -b

a

b

b

c

a

a

c

b

b

a

c

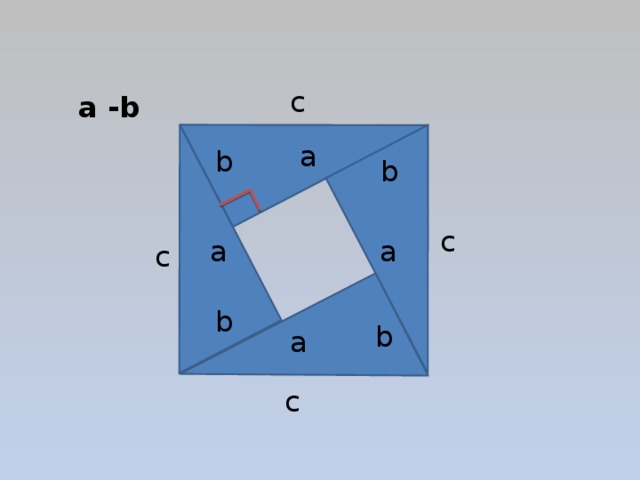
Запишите площадь полученной фигуры

c 2 = 4  ab + (a -b) 2

c 2 = 2ab + a 2 - 2ab + b 2

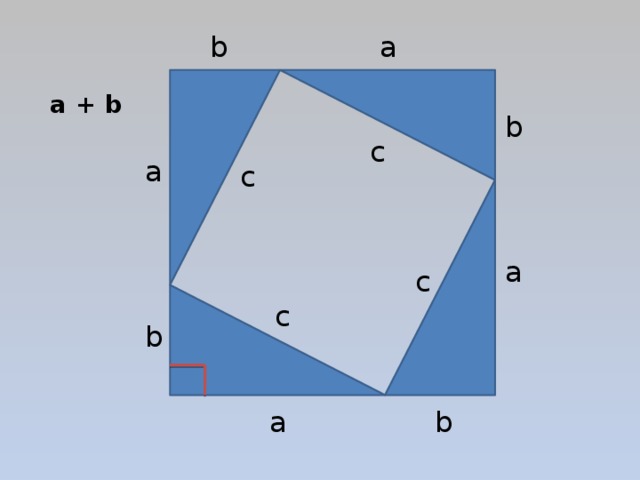
(a+b) 2 =4  ab + c 2

a 2 +b 2 +2ab = 2ab + c 2

a 2 +b 2 = c 2

a 2 +b 2 = c 2

Доказательство индийского математика Бхаскары (труд «Венец науки»)

Доказательство Пифагора

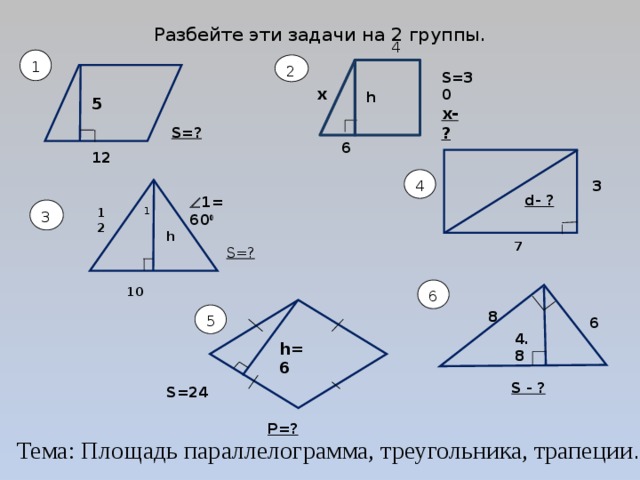
Разбейте эти задачи на 2 группы.

4

1

2

S=30

x

h

5

x-?

S=?

6

12

4

3

d- ?

 1=60 0

3

12

1

h

7

S=?

6

10

8

5

6

4.8

h=6

S - ?

S=24

Р=?

Тема: Площадь параллелограмма, треугольника, трапеции .

1 группа(можем решить): 1, 3, 5

2 группа(пока не можем решить): 2, 4, 6

Почему не можем решить задачи из 2-ой группы?

Практическая работа . Исследование взаимного расположения графиков линейных функций.

Учитель утверждает , что графики функций

y = 2x+5 и y = 2x-3 параллельны, а

y = 2x+5 и y = - 6x+5 пересекаются в т (0;5).

Верно ли это?

Проблема : выяснить как зависит взаимное расположение графиков линейных функций от коэффициентов k и b.

Сильные стороны проблемного обучения

• Способствует развитию познавательной активности, осознанности знаний, предупреждает появление формализма, бездумности.
• Обеспечивает более прочное усвоение знаний;
• Развивает аналитическое мышление.
• Ориентирует на комплексное использование знаний.
• Приучает учащихся, сталкиваясь с противоречиями, разбираться в них, искать решение.

Слабые стороны проблемного обучения

• Значительно больший расход времени на изучение учебного материала;
• Слабая эффективность при усвоении принципиально новых разделов учебного материала, где не может быть применен принцип апперцепции (опоры на прежний опыт);
• При изучении сложных тем, где крайне необходимо объяснение учителем, а самостоятельный поиск оказывается недоступным для большинства школьников.

Рекомендации учителям по созданию проблемных ситуаций на уроке

• Подводить к противоречию с уже известным и предлагать самим находить способ разрешения.
• Побуждать делать сравнения, обобщения, выводы.
• Создавать ситуации включения, используя задания, связанные с их жизненным опытом.
• Использовать задачи с заведомо допущенными ошибками.
• Предлагать практические исследовательские задания.
• Отыскивать различные способы решения одной и той же задачи.
• Излагать различные точки зрения на один и тот же вопрос.
• Учить составлять задачи по статистическим данным своего населённого пункта.
• Использовать тесты с выбором правильного ответа.

Спасибо за внимание!