Способы описания движения. Система отсчета.

Способы описания движения. Система отсчета.

Работу выполнила

Якимович Елена Николаевна

Учитель физики.

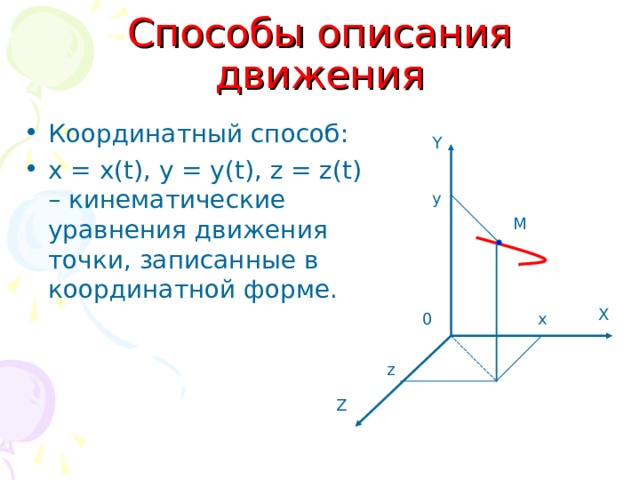
Способы описания движения

• Координатный способ:
• х = х( t) , y = y(t) , z = z(t) – кинематические уравнения движения точки, записанные в координатной форме.

Y

y

M

X

0

x

z

Z

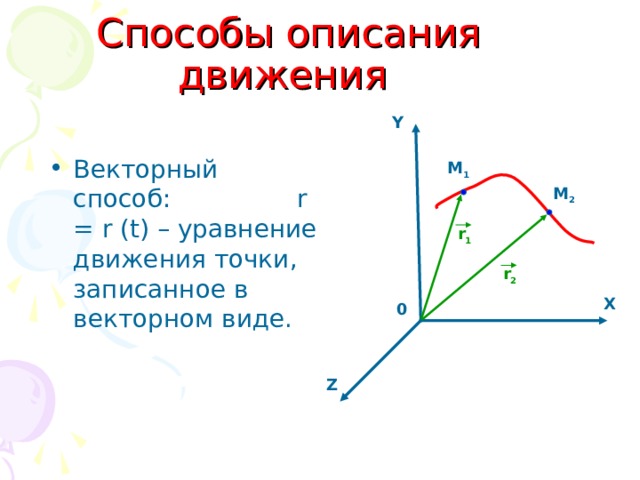
Способы описания движения

Y

• Векторный способ: r = r (t) – уравнение движения точки, записанное в векторном виде.

M 1

M 2

r 1

r 2

X

0

Z

Система отсчета

• Позволяет определить положение материальной точки в пространстве в произвольный момент времени.

1. Тело отсчета

2. Система координат (одномерная, двухмерная, трехмерная)

3. Часы

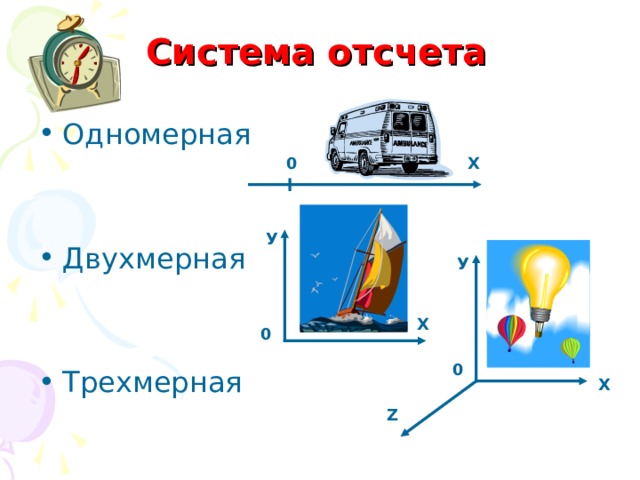
Система отсчета

• Одномерная
• Двухмерная
• Трехмерная

Х

0

У

У

Х

0

0

Х

Z

Траектория - воображаемая линия, соединяющая положения материальной точки (тела) в ближайшие последовательные промежутки времени.

Пройденный путь – это длина траектории.

Перемещение – направленный отрезок, соединяющий начальное положение тела с его конечным положением.

S

В

А

S

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ

Криволинейное

Прямолинейное

Движение, траектория которого кривая линия.

Движение, траектория которого прямая линия

равномерное

неравномерное

равноускоренное

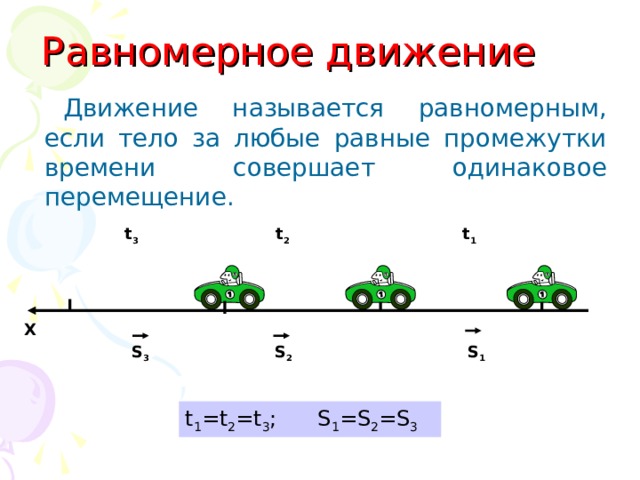
Равномерное движение

Движение называется равномерным, если тело за любые равные промежутки времени совершает одинаковое перемещение.

t 3

t 2

t 1

X

S 1

S 3

S 2

t 1 =t 2 =t 3 ; S 1 =S 2 =S 3

Скорость прямолинейного равномерного движения

• Постоянная векторная величина, равная отношению перемещения точки за любой промежуток времени к значению этого промежутка.

- скорость

- перемещение

t - время

- модуль скорости

S - модуль перемещения

СИ: 1 м/с (метр в секунду)

ВНЕ: 1 км/ч, 1км/с, 1см/с и т.д.

1 м/с – это скорость такого равномерного движения,

при котором движущееся тело за 1 с

совершает перемещение, равное 1 м.

Скорость - векторная величина

Модуль

Направление

Уравнение координаты

Х

0

Х

0

Проекция скорости на координатную ось равна изменению координаты в единицу времени, т.е. скорость показывает как быстро изменяются при движении координаты тела.

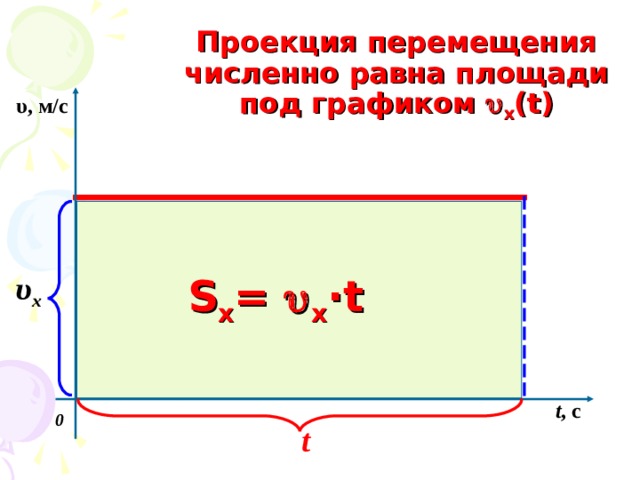
Проекция перемещения численно равна площади под графиком  x ( t)

υ , м/с

S x =  x · t

t , с

0

t

х = 5 t

Х, м

υ = 5 м/с

υ , м/с

20

5

15

10

0

3

t , с

2

1

5

0

t , с

1

2

3

4

Х, м

Х = 10 + 5 t

30

1

2

25

Х = 5 + 5 t

20

3

Х = 5 t

15

α

X = 10 – 5t

10

5

4

3

2

1

0

t , с

4

α 2 α 1 , υ x 3 υ x 2 υ x 1 ). Х, м х 3 х 2 α 3 α 2 х 1 α 1 t , с t " width="640"

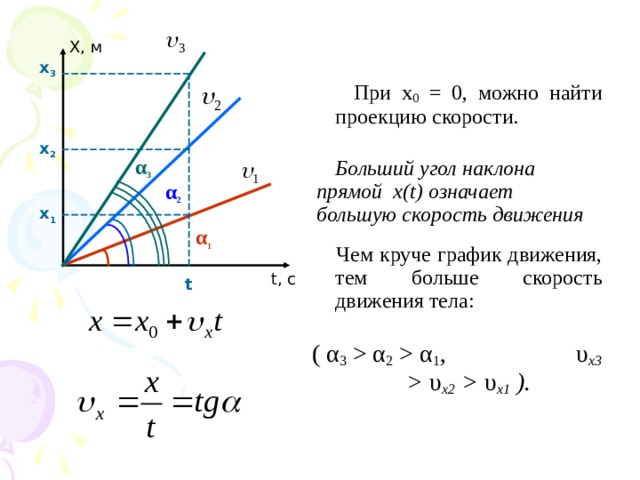
При х 0 = 0, можно найти проекцию скорости.

Больший угол наклона

прямой x ( t ) означает

большую скорость движения

Чем круче график движения, тем больше скорость движения тела:

( α 3 α 2 α 1 , υ x 3 υ x 2 υ x 1 ).

Х, м

х 3

х 2

α 3

α 2

х 1

α 1

t , с

t

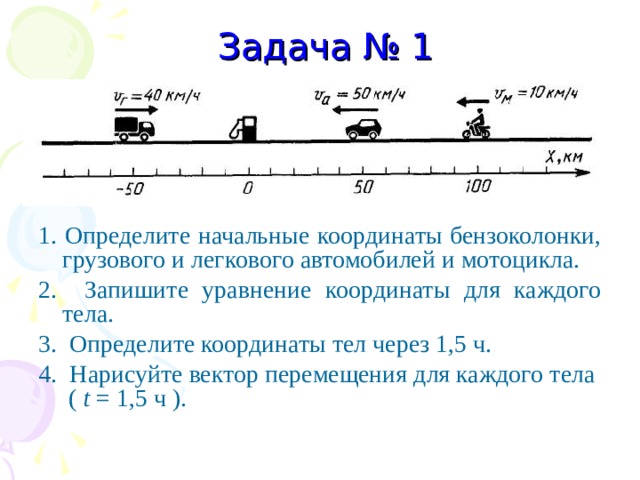
Задача № 1

1. Определите начальные координаты бензоколонки, грузового и легкового автомобилей и мотоцикла.

2. Запишите уравнение координаты для каждого тела.

3. Определите координаты тел через 1,5 ч.

4. Нарисуйте вектор перемещения для каждого тела ( t = 1,5 ч ).

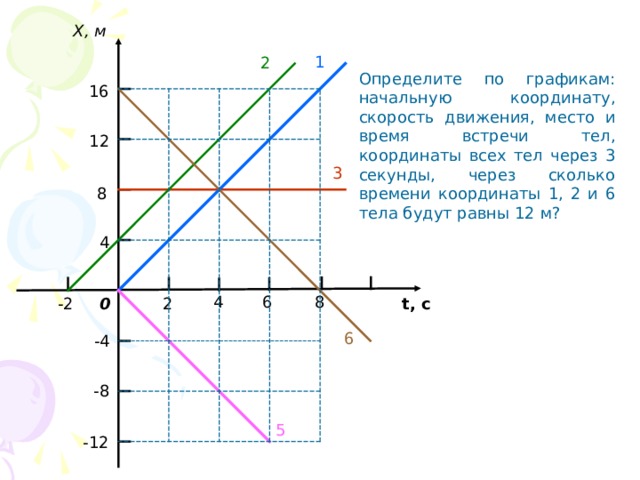
Х, м

1

2

Определите по графикам: начальную координату, скорость движения, место и время встречи тел, координаты всех тел через 3 секунды, через сколько времени координаты 1, 2 и 6 тела будут равны 12 м?

16

12

3

8

4

6

4

8

-2

2

t , с

0

6

-4

-8

5

-12

Задача № 3

Запишите уравнение координаты для каждого тела . Аналитически и графически найдите:

1-й вариант: где и когда 1-е тело догонит 2-е;

2-й вариант: где и когда 1-е тело встретит 3-е;

3-й вариант: где и когда 4-е тело догонит 3-е;

4-й вариант: где и когда 4-е тело встретит 2-е.

Домашнее задание: § 5.