Способы отбора корней в тригонометрических уравнениях

Способы отбора корней в тригонометрических уравнениях

Подготовила

учитель математики

Болотина Татьяна Гавриловна МКОУ « Возовская СОШ» Поныровского района,

Курской области

2017 год

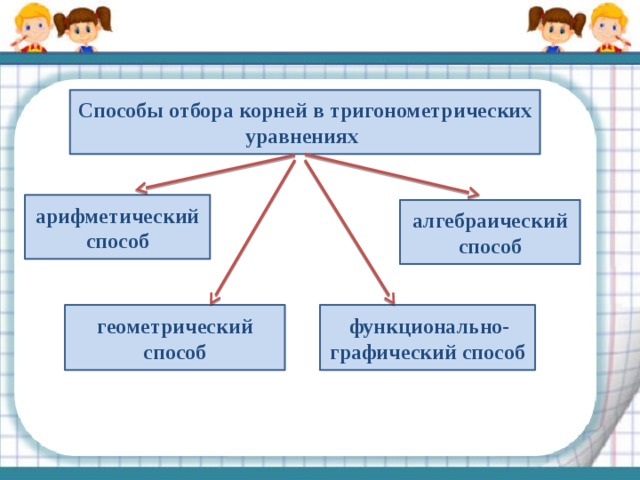
Способы отбора корней в тригонометрических уравнениях

арифметический способ

алгебраический способ

геометрический способ

функционально-графический способ

● Арифметический способ:

а) непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения;

б) перебор значений целочисленного параметра и вычисление корней.

● Алгебраический способ:

а) решение неравенства относительно неизвестного целочисленного параметра и вычисление корней;

б) исследование уравнения с двумя целочисленными параметрами.

● Геометрический способ:

а) изображение корней на тригонометрической окружности с последующим отбором и учетом имеющихся ограничений;

б) изображение корней на числовой прямой с последующим отбором и учетом имеющихся ограничений.

● Функционально-графический способ:

выбор корней с помощью графика простейшей тригонометрической функции.

Арифметический способ (непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения)

Найдите корни уравнения cos x = 0,5, удовлетворяющие неравенству sin x ≤ 0.

Решение

cos x = 0,5, x = + 2πn, n ϵ Z,

Проверим выполнение условия sin x ≤ 0.

Для x = + 2πn, n ϵZ,sin= sin =

Первая серия корней является посторонней.

Для x = - + 2πn, n ϵ Z,sin= sin=.

Ответ: x = + 2πn, n ϵ Z

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие отрезку .

Решение.

а) Решая квадратное уравнение относительно sin, находим,

или

Уравнениетак как

Уравнение

Запишем решение уравнения в виде:

б) Рассмотрим отбор корней на отрезке

• Арифметический способ

Перебирая значения переменной, обозначающей целые числа, мы должны добиться того, чтобы найти все точки внутри промежутка и по одной точке слева и справа от данного промежутка.

Пусть x = + 2πk, k ϵ Z.

при k = -1, x=- ∉ [- π; 2π]

при k = 0, x=

при k = 1, x=∉ [- π; 2π]

Пусть x = + 2πn, n ϵ Z.

при n= -1, x= - ∉ [- π; 2π]

при n = 0, x = ϵ [- π; 2π]

при n = 1, x = ∉ [- π; 2π]

Отрезку [- π; 2π] принадлежат корни , .

[- π; 2π] [- 180°; 360°]

Пусть x = + 2πn, n ϵ Z.

при n = -1, x= - = -330 ° ∉ [- π; 2π]

при n = 0, x = = 30° ϵ [- π; 2π]

при n = 1, x = =390 ° ∉ [- π; 2π]

Пусть x = + 2πk, k ϵ Z.

при k = -1, x=- = -210 ° ∉ [- π;2π]

при k = 0, x=

при k = 1, x== 510 ° ∉ [- π; 2π]

Отрезку [- π; 2π] принадлежат корни ,

Рассмотрим отбор корней с помощью координатной прямой.

Покажем дополнительные точки, которые находятся внутри отрезка [- π; 2π], слева и справа от него

n= -1 ,x

k = - 1 , x

n = 0 , x

k = 0 , x

Отрезку [- π; 2π] принадлежат корни , , .

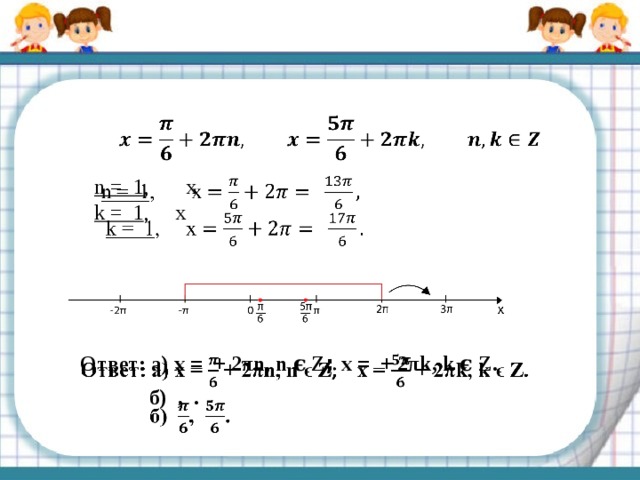
n = 1 , x

k = 1 , x

Ответ: а) х = + 2πn, n ϵ Z ; х = + 2πk, k ϵ Z.

б) , .

2. Алгебраический способ .

Корни уравнения должны принадлежать отрезку [- π; 2π].

Это значит, что – π ≤ x ≤ 2π.

Пусть x = + 2πk, k ϵ Z.

Пусть x = + 2πn, n ϵ Z

Тогда – π ≤ + 2πk ≤ 2π;

Тогда – π ≤ + 2πn ≤ 2π;

- 2πk ≤ ;

- 2πn ≤ ;

- n ≤ ;

- k ≤ ;

k = 0; x= .

n = 0; x= .

Отрезку [- π; 2π] принадлежат корни , .

3. Геометрический способ

( Отбор корней с помощью тригонометрической окружности)

sin x =

π -

x

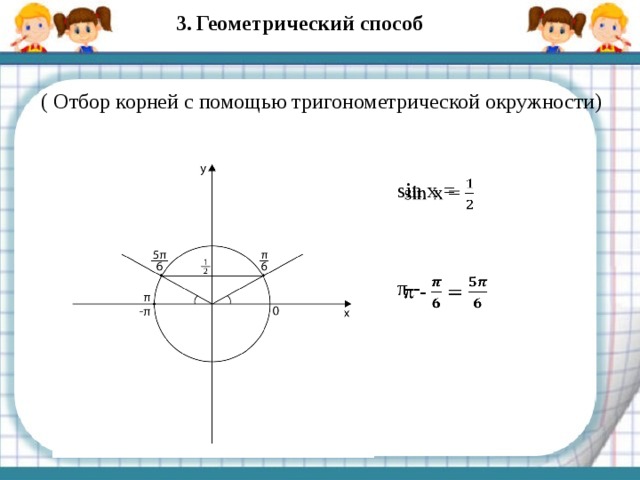
3. Геометрический способ

( Отбор корней с помощью тригонометрической окружности)

sin x =

π -

x

Отрезку [- π; 2π] принадлежат

корни , .

3. Функционально-графический способ

Корни принадлежащие отрезку [- π; 2π], отберем по графику y= sin x. Прямая y = пересекает график в двух точках, абсциссы которых принадлежат отрезку [- π; 2π]. Так как период функции y = sin x равен 2π, то эти абсциссы равны π - =

Отрезку [- π; 2π] принадлежат корни , .

а) Решите уравнение 2sin 4 x + 3 cos 2x + 1 = 0

б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 3π]

2 sin 4 x + 3(1 – 2sin 2 x) +1 = 0

2 sin 4 x – 6 sin 2 x + 4 = 0

sin 4 x – 3 sin 2 x + 2 = 0, сделаем замену.

sin 2 x = t

t 2 – 3 t 2 + 2 = 0

По теореме Виета или через дискриминант

t 1 = 1 или t 2 = 2

[π; 3π]

sin 2 x = 1 или sin 2 x = 2

sinx = ±1 или sinx = ± - уравнение корней не имеет

sinx = ±1

x = + πn, n ϵ Z

Геометрический способ

Отбор по окружности. На числовой окружности нужно показать нужный нам отрезок.

x ϵ [π; 3π]

Отберем все точки которые попадают на этот отрезок

x = π + = ,

x = 2π + =

Рассмотрим отбор корней с помощью координатной прямой.

Покажем дополнительные точки, которые находятся внутри отрезка [π; 3π] , слева и справа от него

x = + πn, n ϵ Z

n = 0, x =

x = + πn, n ϵ Z n = - 1, x = - π = -

n = 1, x = + π = ϵ[π; 3π]

n = 2, x = + 2π= ϵ[π; 3π]

Алгебраическийспособ

Корни должны попадать в отрезок [π; 3π]

Это значит, что π ≤ x ≤ 3π

π ≤ + πn ≤ 3π

π - ≤ πn ≤ 3π -

≤ πn≤

≤ n≤

Это значит, что 0,5 ≤ n ≤ 2,5

n = 1; x = , n = 2; x = .

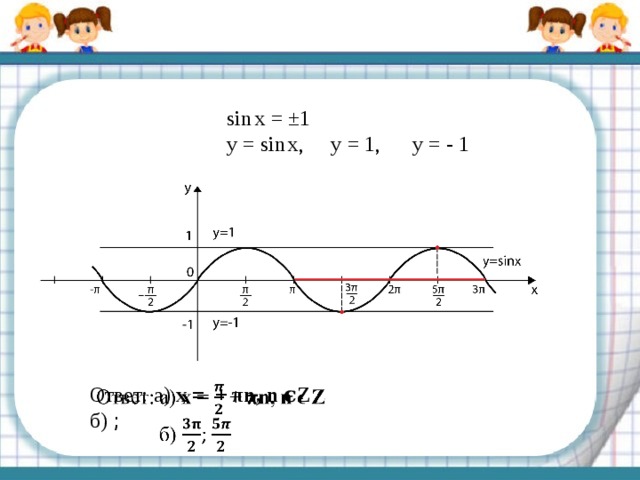
sin x = ±1

y = sin x, y = 1, y = - 1

Ответ: а) x = + πn, n ϵZ

б) ;

Спасибо за внимание