Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №1 г. Южи Ивановской области
Исследовательская работа по теме:
«Стандартные и нестандартные методы решения квадратных уравнений»
Работа ученицы 9 класса
Зубкова Д.
Руководитель: Чурина
Елена Вениаминовна,
Учитель математики
Работа допущена к защите «_____» _______________ 202____г. Подпись руководителя проекта ____________________(__________________)
Г. Южа
2021 год
Содержание
Актуальность
Цель и задачи работы
1. История возникновения квадратных уравнений
2.Определение квадратного уравнения
3. Стандартные методы решения квадратного уравнения
3.1.Разложение левой части на множители
3.2.Решение квадратного уравнений по формуле
3.3. Решение уравнений с использование теоремы Виета (прямой и обратной)
4. Нестандартные методы
4.1.Метод выделения полного квадрата
4.2.Графическое решение квадратного уравнения
4.3. Решение квадратных уравнений с помощью свойств коэффициентов.
4.4.Геометрический способ.
4.5. Решение уравнений с использованием теоремы Безу
5. Исследование
6. Выводы
7.Заключение.
Актуальность
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
Теория уравнений занимает ведущее место в алгебре и математике в целом. Сила теории уравнений в том, что не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Квадратное уравнение представляет собой большой и важный класс уравнений, решающих как с помощью формул, так и с помощью элементарных функций.
В учебниках мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем решение по формулам. Вместе с тем, современные научно – методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.
Все это заинтересовало меня, и поэтому, для своей исследовательской работы выбрал тему «Способы решения квадратных уравнений».
Цель исследовательской работы: выявить способы решения квадратных уравнений, узнать можно ли решить любое квадратное уравнение данными способами и выделить особенности и недостатки этих способов.
Задачи исследовательской работы: проанализировать источники литературы для выявления способов решения квадратных уравнений, показать различные способы решения квадратных уравнений.
Задачи:
Познакомиться с историческими фактами, связанными с данным вопросом.
Описать технологии различных существующих способов решения уравнений второй степени.
Провести анализ этих способов, сравнить их.
Привести примеры применения различных способов решения уравнений.
Создать дидактический материал по решению квадратных уравнений различными способами.
Объект исследования: квадратные уравнения.
Предмет исследования: способы решения квадратных уравнений.
Гипотеза: любое квадратное уравнение можно решить всеми существующими способами.
Практическая значимость: квадратные уравнения – это фундамент, на котором построен курс алгебры. К решению квадратных уравнений сводятся решения дробно-рациональных уравнений и текстовых задач, находят широкое применение при решении тригонометрических, логарифмических, иррациональных уравнений. Начинают изучать решение квадратных уравнений в 8 классе и решают их до окончания вуза.
Методы исследования: анализ литературы, социологический опрос, наблюдение, сравнение и обобщение результатов
История возникновения квадратных уравнений
Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений. Правило решения таких уравнений, изложенное в вавилонских текстах, совпадают с современным, однако неизвестно, каким образом дошли они до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Задачи на квадратные уравнения встречаются уже в 499 г. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Часто они были в стихотворной форме.
Вот одна из задач знаменитого индийского математика XIIв. Бхаскары.
Обезьянок резвых стая
Власть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая.
Сколько ж было обезьянок
Ты скажи мне, в этой стае?
Квадратные уравнения в Европе 13-17 вв. Формулы решения квадратных уравнений в Европе были впервые изложены в «Книге абака», написанной в 1202 году итальянским математиком Леонардом Фибоначчи. Эта книга способствовала распространению алгебраических знаний не только в Италии, но и Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники 14-17 веков. Общее правило решения квадратных уравнений вида было сформировано в Европе лишь в 1544 году Штифелем. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики 16 века.учитывали помимо положительных, и отрицательные корни. Лишь в 17 веке благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
«Квадраты равны корням», т.е. ax2 + c =bx(5х2=10х).
«Квадраты равны числу», т. е. ax2=c(5x2=80).
«Корни равны числу», т. е. ax=c(4х=20).
«Квадраты и числа равны корням»,т.е.ax2+c=bx(х2+ 10х=39).
«Квадраты и корни равны числу», т. е. ax2+bx=c(x2+21=10x).
Корни и числа равны квадратам», т. е. bx+c=ax2 (3х+4=х2)
Его решение, конечно, не совпадает полностью с нашим. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х2+bх=с, при всевозможных комбинациях знаков коэффициентов b, c , было сформулировано в Европе в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых вXVIв. учитывают, помимо положительных, и отрицательные корни. Лишь вXVIIв. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была сформулирована им впервые в 1591г.
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета ещё далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
2.Определение квадратного уравнения и его виды
Квадратным уравнением называется уравнение вида
ax2 + bx + c = 0,
где х- переменная, а, b и с-некоторые числа, при этом, а ≠ 0
Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени.
Квадратное уравнение называют приведённым, если коэффициент а равен 1.
Квадратное уравнение называется не приведённым, если коэффициент а отличен от 1.
х2 + px +q = 0 – стандартный вид приведённого квадратного уравнения.
Кроме приведённых и не приведённых квадратных уравнений различают также полные и неполные уравнения.
Полное квадратное уравнение – это квадратное уравнение, у которого коэффициенты b и c отличны от 0.
Неполное квадратное уравнение – это уравнение, у которого хотя б
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
Неполное квадратное уравнение - это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Корнем квадратного уравнения ах2 + bx +c = 0 называют всякое значение переменной х, при котором квадратный трёхчлен ах2 + bx +c обращается в нуль; такое значение переменной х называют также корнем квадратного трёхчлена.
Корень квадратного уравнения ах2 + bx + c = 0 – это значение переменной х, при котором уравнение обращается в верное равенство.
Решить квадратное уравнение – это значит найти все его корни или убедиться в том, что корней нет.
Квадратное уравнение может иметь два корня, один корень и не иметь корней.
3.Стандартные методы решения квадратных уравнений:
Разложение левой части уравнения на множители.
Разложение на множители уравнения – это процесс нахождения таких членов или выражений, которые, будучи перемноженными, приводят к начальному уравнению.
Пример
Решим уравнение х2+10х-24=0.
Разложим левую часть уравнения на множители:
Х2+10х-24=х2+12х-2х-24=х(х+12)-2(х+12)=(х+12)(х-2).
Следовательно, уравнение можно переписать так:
(х+12)(х-2)=0.
Так как произведение равно нулю, то по крайней мере один из множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х=2,а уравнение х2+10х-24=0.
Этот способ дает возможность сразу увидеть корни уравнения, если правильно вычислить слагаемых для группировки
Решение квадратного уравнения по формуле
Вывод формулы:
Умножим обе части уравнения ax2+bx+c=0 , а ≠ 0, на 4а и, следовательно, имеем :
4а2х2+4аbc+4ac=0
((2ax)2+2ax ∙ b + b2)-b2+4ac=0
(2ax+b)2=b2-4ac
2ax+b= ±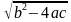
2ax =-b±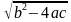
X1,2=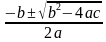
Выражение b2- 4 ac называют дискриминантом и обозначают D, причем
Если D0, то уравнение ax2+bx+c=0 имеет два различных корня;
Если D=0, то два одинаковых корня;ЕслиD
Решение квадратных уравнений по формуле с четным коэффициентом.
Если второй коэффициент уравненияb = 2k– четное число, то формулу корней 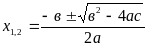 можно записать в виде
можно записать в виде
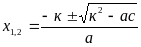
Приведенное уравнение х2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней принимает вид
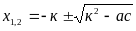
Формулу удобно использовать, когда р— четное число.
Пример: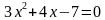
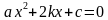 ,
,
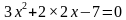 ,
,
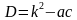 ,
,
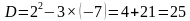 ,
,
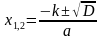 ,
,
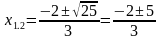 ,
,
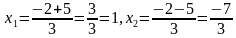 .
.
Если выучить формулы, то этот способ можно применить ко всем квадратным уравнениям.
Решение уравнений с использование теоремы Виета (прямой и обратной)
1)Как известно, приведенное квадратное уравнение имеет вид:
x2+ px + q=0 (1)
Его корни удовлетворяют теореме Виета, которая при а=1 имеет вид
x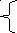 1x2= q
1x2= q
x1+x2 = -p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
А) Если свободный член q приведенного уравнения (1) положителен (q 0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p.
Если p0, то оба корня отрицательные, если p
Например,
х2-3x+2=0; x1 = 2 bx2=1, так как q = 20 и q = 2 0 и p = – 3
х2 +8х + 7 = 0; х1 = – 7 и х2 = – 1, так как q = 7 0 и p = 8 0.
Б) Если свободный член q приведенного уравнения (1) отрицателен (q 0. Например, х2 + 4х – 5 = 0; х1 = – 5 и х2 = 1, так как q = – 5 0; х2 – 8х – 9 = 0; х1 = 9 и х2 = – 1, так как q = – 90.
2) Теорема Виета для квадратного уравнения ax2+bx+c=0 имеет вид :
х1х2 = 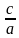 ,
,
х1+х2 = - 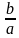 .
.
Справедлива теорема, обратная теореме Виета:
Если х1 и х2 таковы, что х1+х2 = -p, х1х2 = q, то х1 и х2 – корни квадратного уравнения
х2 + px + q = 0.
Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.
Примеры
Решить уравнение x2-9x+14=0
Попробуем найти два числа х1 и х2, такие, что
х 1 + х2 = 9
1 + х2 = 9
х1х2 = 14
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
2.Решить уравнение :x2+3x-28 =0
Попробуем найти два числа х1 и х2 , такие, что
х1+х2= - 3
х1х2 = - 28
Нетрудно заметить, что такими числами будут - 7 и 4. Они и являются корнями данного уравнения.
Достаточно легкий способ, дает возможность сразу увидеть корни уравнения, но легко находятся только целые корни.
Нестандартные методы решения квадратных уравнений:
1.Метод выделения полного квадрата
Решим уравнение х2 + 6х - 7 = 0.
Выделим в левой части полный квадрат:
х2 + 6х - 7 = х2 + 2*х * 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
тогда, данное уравнение можно записать так
(х + 3)2 - 16 =0,
(х + 3)2 = 16,
х + 3=4 или х + 3 = -4
х1 = 1 х2 = -7
Ответ: 1; -7.
За минимальное количество действий можно найти корни уравнений, если правильно найти все слагаемые для выделения полного квадрата.
2. Решение квадратного уравнения графическим способом
Если в уравнении : х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = - px – q.
Построим графики зависимости у = х2 и у = - px - q.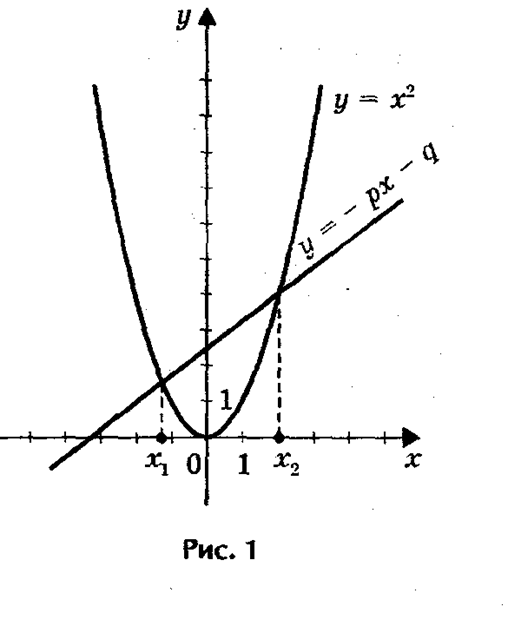
График первой зависимости – парабола, проходящая через начало координат.
График второй зависимости – прямая.
Возможны следующие случаи :
-прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут качаться (только одна общая точка), т.е. уравнение имеет одно решение;
-прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Пример
Решим графически уравнение : х2 - 3х - 4 = 0
Решение. Запишем уравнение в виде : х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13).
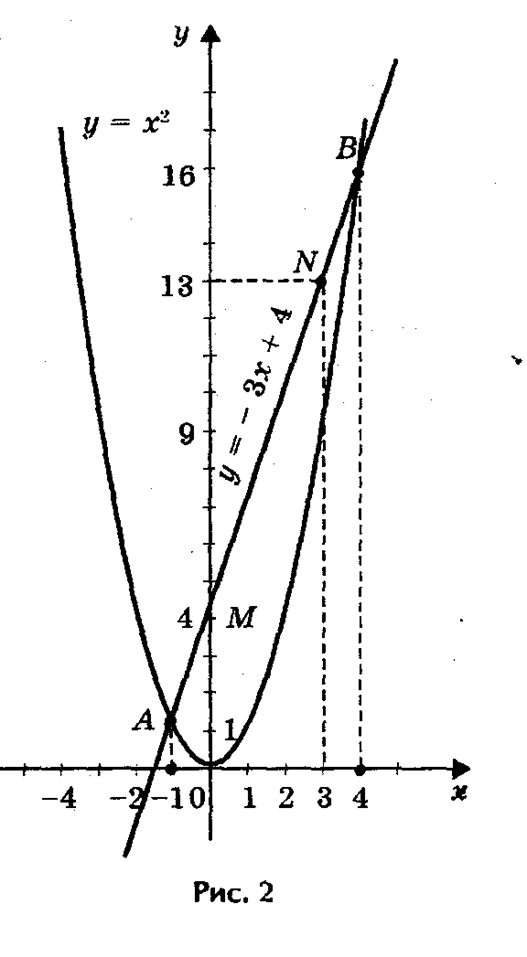
Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = -1 и х2 = 4.
Ответ.х1 = -1, х2 = 4.
Графический способ решения квадратных уравнений с помощью параболы не всегда удобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точность получаемых результатов невелика.
3.Решение квадратных уравнений с помощью свойств коэффициентов.
Пусть дано квадратное уравнение
ах² + bх + с = 0, где а ≠ 0.
А) Если а+ b+ с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,х2= с/а.
Б) Если а - b + с = 0, или b = а + с, то х1= – 1, х2 = – 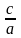 .
.
Решим уравнение 345х²– 137х – 208 = 0.
Решение. Так кака + b+ с = 0 (345 – 137 – 208 = 0), то
Х1= 1, х2= c/a= -208/345.
Ответ: 1; -208/345.
Решим уравнение 132х2 - 247х + 115 = 0
Решение. Т. к. а-b+с = 0 (132 – 247 +115=0), то
х1= 1, х2= 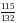
Ответ: 1; 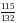
Этот способ не требует особых усилий, ноподходит только к некоторым уравнениям.
4.Геометрический способ решения квадратных уравнений
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми. Уравнение х2 + 10х = 39
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39».
Строим квадрат со стороной х и на его сторонах – четыре прямоугольника высотой 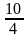 . В углах фигуры построим четыре квадрата со стороной
. В углах фигуры построим четыре квадрата со стороной 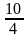 . В углах фигуры построим четыре квадрата
. В углах фигуры построим четыре квадрата 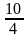 .
.









Подсчитаем площадь получившегося большого квадрата:
X2 + 4 • 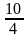 • (
• (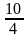 )2= x2 + 10x + (
)2= x2 + 10x + (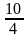 )2 • 4
)2 • 4
По условию x2 + 10x = 39, т.е. площадь большого квадрата равна
39 + ( 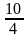 )2 • 4 = 39 + + 25 =64.
)2 • 4 = 39 + + 25 =64.
Значит, его сторона равна 8, тогда x + 2 • ( 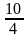 ) = 8, x = 3 (Ал–Хорезми не признавал отрицательных чисел)
) = 8, x = 3 (Ал–Хорезми не признавал отрицательных чисел)
А вот, например, как древние греки решали уравнение y2 + 6y – 16 = 0
Решение представлено на рис., где у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = - 8.
5. Решение уравнений с использованием теоремы Безу
Теорема Безу. Если уравнение a0xn + a1xn-1 … + an-1x + an = 0, где все коэффициенты целые, имеет целые корни, то это делители свободный член.
Следствие 2: Если b является корнем многочлена f (x), то этот многочлен делится на (x-b) без остатка.
Теорема Безу даёт возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого уже на единицу меньше.
Таким образом, один корень найден и далее находятся уже корни многочлена, степень которого на единицу меньше степени исходного многочлена. Иногда этим приёмом – он называется понижением степени – можно найти все корни заданного многочлена.
Пример
Решить квадратное уравнение: х2 – 4х + 3 = 0
f(x) = x2 – 4x + 3
Решение :
Делители свободного члена ±1, ±3.
Проверим 1, подставив в уравнение 1 – 4 + 3 = 0. Значит 1 – это корень данного уравнения. Тогда квадратный трёхчлен х2 - 4х + 3 делится нацело на (х-1)Разделим f(x) на (x-1), получим:
Х 2-4х+3 х-1
2-4х+3 х-1
Х 2-х х-3
2-х х-3
-3х+3
 3х+3
3х+3
0
Х2 – 4х + 3 = (х-1)(х-3)
(х-1)(х-3) = 0x – 1 = 0или х-3 =0
х1 = 1 или х2=3
Ответ: х1 = 1, х2=3.
5. Исследование
Я провела опрос одноклассников:
1. Надо ли уметь решать квадратное уравнение?
2. Часто ли ты решаешь квадратное уравнение?
3. Известны ли тебе способы решения квадратных уравнений, кроме как решение уравнений по формулам?
Результаты опроса выглядят так:
1 вопрос:
2 вопрос:
3вопрос:
6.Выводы:
1.Квадратные уравнения умели решать ещё более трех тысяч лет назад. Способы решения были сложными.
2.Способов решения квадратных уравнений очень много. Я остановилась на 8 из них. Нужно отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на ОГЭ.
3. Для того чтобы усвоить все методы решения уравнений, нужно решить несколько уравнений изучаемым способом. А для этого нужны задания. Я создала небольшой дидактический материал для отработки навыков решения квадратных уравнений по каждому из рассмотренных способов.
4. Я опровергла свою гипотезу. Есть способы решения квадратных уравнений, которые применимы только для отдельных видов этих уравнений.
5. Квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения с 8 класса. Эти знания могут пригодиться нам на протяжении всей жизни.
Заключение
Человечество прошло длинный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание всё более полным и совершенным.
Уравнения – язык алгебры, квадратные уравнения – это фундамент, на котором построено величественное здание алгебры. Изученные способы решения квадратных уравнений будут применяться и при дальнейшем изучении математики, при решении уравнений, сводящихся к решению квадратных.
В ходе выполнения работы с поставленной целью и задачами я справилась, мне удалось обобщить и систематизировать изученный материал по выше указанной теме. Проанализировав все новые способы решения квадратных уравнений, стало очевидным, что нельзя однозначно сказать, какой именно метод наиболее удобен или совершенен. Некоторые (такие как, решение с использованием теоремы Безу) удобно применять, когда коэффициенты невелики, другие – допускают большие коэффициенты ( например, учёт коэффициентов): графический не всегда точен, а геометрический понятен, но громоздок. Можно сделать вывод, что все способы надо иметь в своем арсенале и применять их по мере необходимости с точки зрения рациональности решения.
Данная работа помогла мне обобщить способы решения квадратных уравнений, которые изучают и не изучают в школе.
Литература:
1. Алгебра: учебник для 8 класса общеобразовательных учреждений / А45 Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 11-е издание – М.: Просвещение, 2003. – 238 с.: ил. – ISBN 5-09-011880-9.
2. Гусев В. А., Мордкович А. Г. Математика: Справочные материалы: Книга для учащихся. – М.: Просвещение, 1988
3. Глейзер Г. И. История математики в школе. – М.: просвещение, 1982
4. Математика. Алгебра. Функции. Анализ данных. 8 класс: Учебник для общеобразовательных учреждений / Г. В. Дорофеев и др. – М.: Дрофа, 2004
5. Мордкович А. Г. М 79 Алгебра. 8 класс: В двух частях. Ч.1: Учебник для общеобразовательных учреждений. – 4-е издание – М.: Мнемозина, 2002. – 223 с.: ил. – ISBN 5-346-00148-4.
6. Окунев А. К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. – М.: Просвещение, 1972
7. Энциклопедический словарь юного математика для среднего и старшего возраста. -2-е издание- М.: «Педагогика», 1989. – 132с.
Приложение 1
Дидактический материал к работе.
1. Решите квадратное уравнение разложением левой части на множители:
а) х2 – х = 0; е) х2 – 4х + 4 = 0;
б) х2 + 2х = 0; ж) х2 + 6х + 9 = 0;
в) 3 х2 – 3х = 0; з) х2 + 4х +3 = 0;
г) х2 – 81 = 0; и) х2 + 2х – 3 = 0.
д) 4 х2 –  = 0;
= 0;
2. Решите уравнения по формуле:
а) 2х2 – 5х + 2= 0 г) 4х2 – 12х +9 = 0
б) 6х2 + 5х + 1=0 д) 10х2 – 6х + 0,9 = 0
в) 3х2 – 7х – 1 = 0 е) 2х2 – 3х + 2 = 0
3. Не решая квадратного уравнения, определите знаки его корня:
1) х2 – 2х – 15 = 0 7) х2 – 2х + 1 = 0
2) х2 + 2х – 8 = 0 8) х2 + 4х + 4 = 0
3) х2 + 10х + 9 = 0 9) х2 – 6х + 9 = 0
4) х2 – 12х + 35 = 0 10) 4х2 + 7х – 2 = 0
5)3 х2 +1 4х + 16 = 0 11) 5х2 – 9х – 2 = 0
6) х2 – 5х + 6 = 0 12) х2 – 11х + 15 = 0
4. Решите уравнения, используя свойства коэффициентов:
5х2 – 7х + 2 = 0 5) 839х2 – 448х – 391 = 0
3х2 + 5х – 8 = 0 6) 939х2 + 978х +39 = 0
11х2 + 25х – 36 = 0 7) 313х2 + 326х + 13 = 0
11х2 + 27х +16 = 0 8) 2006х2 – 2007х + 1 = 0
5. Решите уравнения по формуле четного коэффициента:
4х2 – 36х + 77 = 0 3) 4х2 + 20х + 25 = 0
15х2 – 22х – 37 = 0 4) 9х2 – 12х + 4 = 0
6. Решите приведенные квадратные уравнения по формуле:
х2 – 8х – 9 = 0 3) х2 + 18х + 81 = 0
х2 + 6х – 40 = 0 4) х2 - 56х + 64 = 0
8. Решите графически уравнения:
1) х2 –х – 6 = 0; 4) х2 –2х – 3 = 0;
2) х2 –4х + 4 = 0; 5) х2 + 2х – 3 = 0;
3) х2 + 4х +6 = 0; 6) 4х2 –4х – 1 = 0.





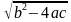
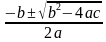
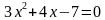
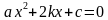 ,
,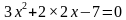 ,
,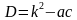 ,
,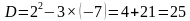 ,
,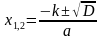 ,
,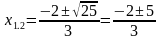 ,
,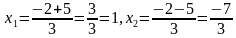 .
.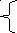 1x2= q
1x2= q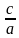 ,
,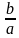 .
.

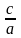 .
.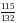
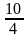 . В углах фигуры построим четыре квадрата со стороной
. В углах фигуры построим четыре квадрата со стороной 









