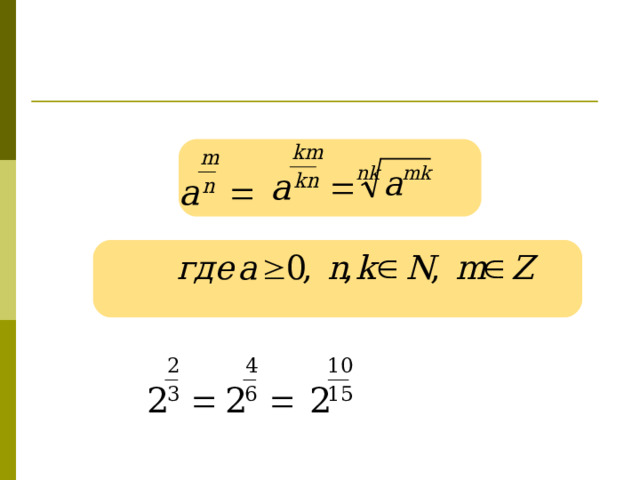Степень с рациональным показателем и ее свойства.

«Люди, незнакомые с алгеброй, не могут представить себе тех удивительных вещей, которых можно достигнуть… при помощи названной науки». Г.В.Лейбниц

История возникновения степени числа
В знаменитой книге «Арифметике» Диофант Александрийский описывал первые натуральные степени

Одним из первых, кто в конце XYI -начале XYII века
принял шаги к построению современной теории степеней,
был Нидерландский математик Симон Стевин.
Он обозначал неизвестную величину кружком
, а внутри его указывал
показатель степени.
Например:
1
2
3
,
,
,
В его записи обозначали x, x², x³ .

У Рене Декарта в его «Геометрии» (1637) мы находим современное обозначение степеней а 2 ,а 3 ,...

Повторение
Степень с целым показателем
Степенью числа а с натуральным показателем n , большим 1, называется произведение n множителей, каждый из которых равен а
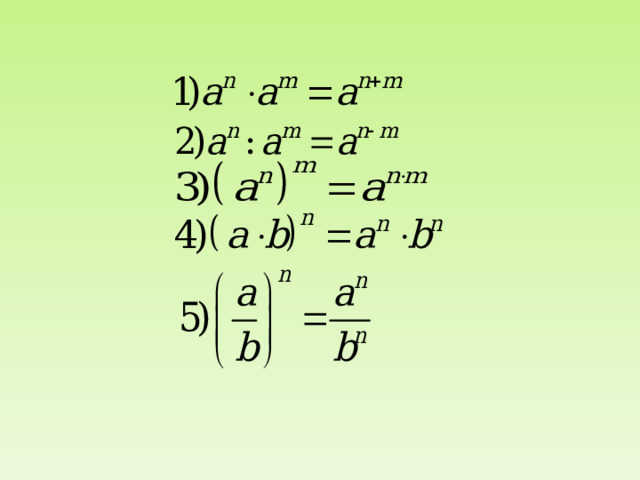
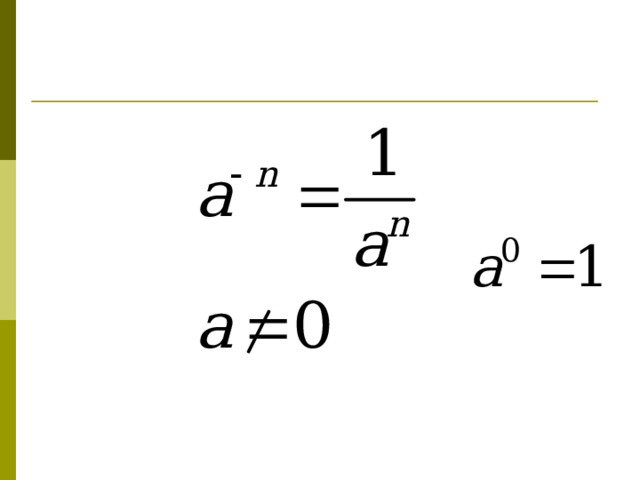
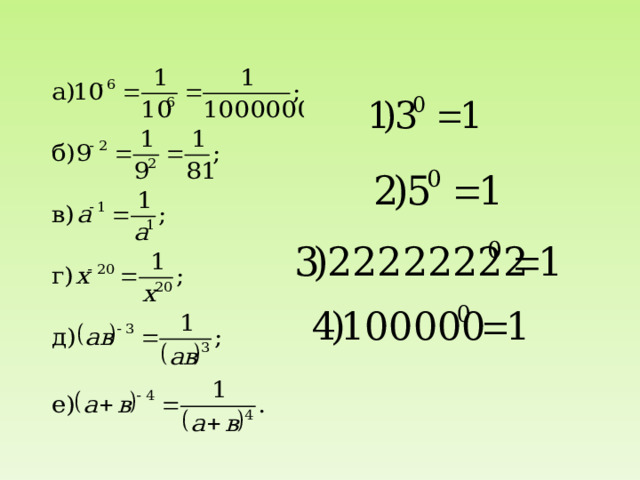

Арифметический корень натуральной степени Определение
Корнем n- ой степени из числа a называется такое число, n- я степень которого равна a .

АРИФМЕТИЧЕСКИЙ КОРЕНЬ
n -Й СТЕПЕНИ ИЗ ЧИСЛА а
а – ПОДКОРЕННОЕ ВЫРАЖЕНИЕ

Тождества
ДЕЙСТВИЕ, ПОСРЕДСТВОМ КОТОРОГО ОТЫСКИВАЕТСЯ КОРЕНЬ n – Й СТЕПЕНИ, НАЗЫВАЕТСЯ ИЗВЛЕЧЕНИЕМ КОРНЯ n – Й СТЕПЕНИ.

Примеры

Устно:
 1, m 1) " width="640"
1, m 1) " width="640"
Свойства корня n -ой степени (для n ∈ N , m ∈ N , n 1, m 1)

Понятие степени с рациональным показателем
Примеры

Представьте степень с дробным показателем в виде корня:
1.
2.
3.
не имеет смысла
4.
5.

1.
Представьте в виде степени с дробным показателем:
2.
3.
4.
5.
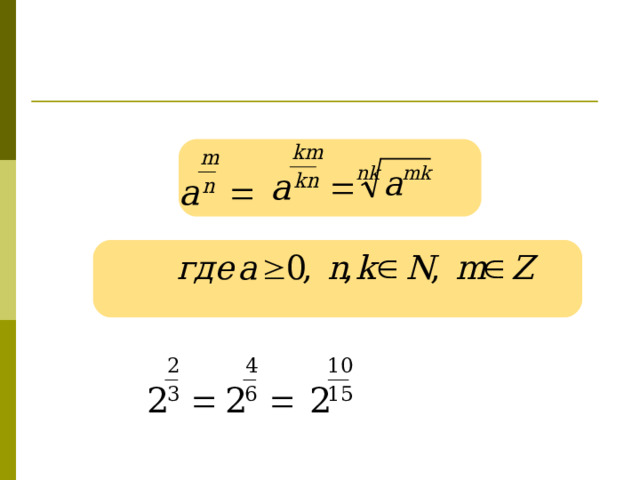

Свойства степени с рациональным показателем (для p ∈ R , q ∈ R )

Решаем номера из учебника:
№№ 118, 119, 120, 121,123,124

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их
(Д. Пойа)

Домашняя работа
Параграф 10
№№ 122, 125, 127













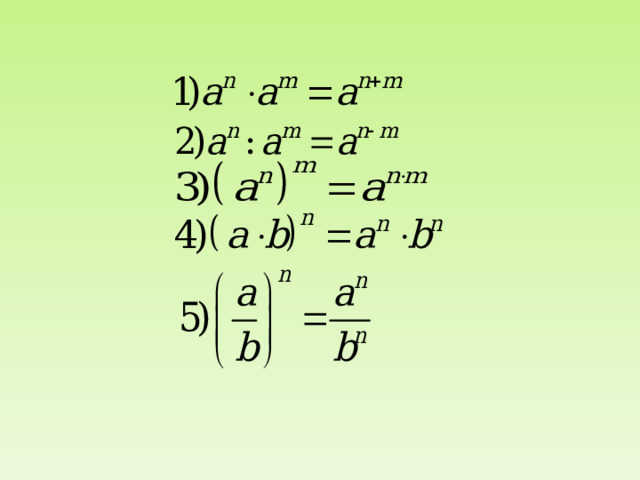
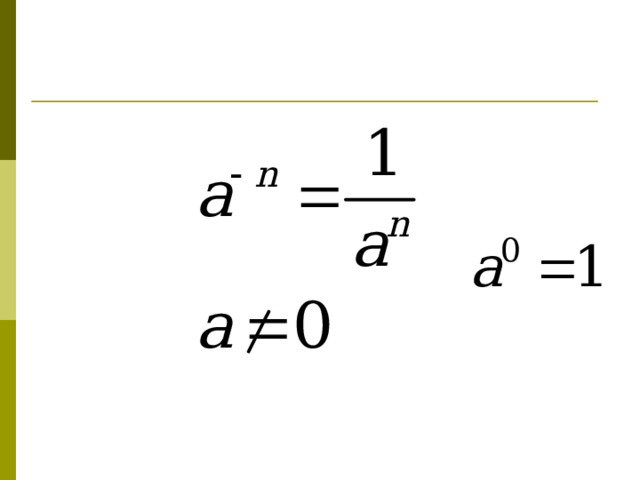
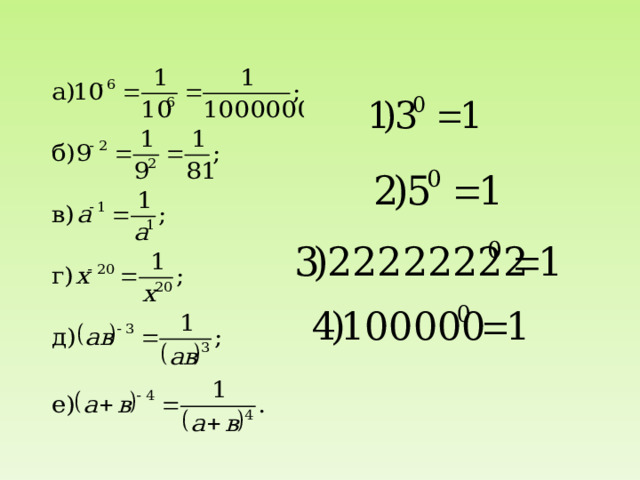





 1, m 1) " width="640"
1, m 1) " width="640"