| № | Этап урока | Деятельность учителя | Деятельность учащихся |
| 1. | Мотивация к учебной деятельности | Доброе утро! Сегодняшний урок мне хотелось бы начать словами Юрия Ивановича Смирнова «Если ты услышишь, что кто−то не любит математику, не верь. Ее нельзя не любить — ее можно только не знать».
| Настраиваются на работу, получают позитивный заряд, концентрируют внимание
Записывают в тетради число и классная работа |
| 2. | Проверка домашнего задания | На последних уроках вы научились находить члены арифметической прогрессии. Фронтальный опрос - Дайте определение арифметической прогрессии (Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом) - Напишите формулу для нахождения n−го члена арифметической прогрессии 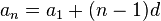
Начнем наше занятие, как всегда, с маленькой математической разминки. Задания будут по очереди появляться на экране, вы решаете их устно Устный счет |
Отвечают на вопросы учителя
Отвечают устно |
| 3. | Актуализация знаний | Самостоятельная работа по теме: «Арифметическая прогрессия» Вариант 1 1. В арифметической прогрессии (аn) известны а1 = – 0,8, d = – 0,4. Найдите а2, а3, а7 . 2. Арифметическая прогрессия (аn) задана последовательностью: 3; 7; … . Найдите d , а3, а4, а11. 3. Найдите первый член а1 арифметической прогрессии (аn), если а8 = 19, d = 1,2 Вариант 2 1. В арифметической прогрессии (аn) известны а1 = – 12,5, d = 1,5. Найдите а2, а3, а10 . 2. Арифметическая прогрессия (аn) задана последовательностью: 81; 77; … . Найдите d , а3, а4, а16. 3. Найдите первый член а1 арифметической прогрессии (аn), если а16 = –11, d = –1. | Выполняют самостоятельно, меняются листочками. Взаимопроверка |
| 4. | Физминутка. | Раз – подняться, подтянуться, Два – согнуться, разогнуться, Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире. Пять – руками помахать, Шесть – успокоиться и сесть. | Выполняют задание учителя |
| 5. | Организация познавательной деятельности
| Я хочу предложить вам решить задачу, которая связана с детскими годами замечательного немецкого математика Карла Гаусса (1777–1855 гг.). Когда ему было 9 лет, учитель задал эту задачу всему классу, чтобы дети не мешали ему проверять письменные работы учеников другого класса, думая, что на это задание у ребят уйдёт весь урок. Но через 1 минуту Карл произнес: «Я уже решил…» – и сдал работу. Давайте попробуем повторить этот опыт. Итак, задание: Найти сумму чисел 1 + 2 + 3 + 4 + … + 100 Задача очень непроста:
Как сделать, чтобы быстро
От единицы и до ста
Сложить в уме все числа?
Пять первых связок изучи,
Найдёшь к решению ключи.  - Данный ряд является арифметической прогрессией? - Мы с вами что нашли? – Значит, тема нашего урока Сумма n первых членов арифметической прогрессии (стр. 239, п. 4.3) Давным-давно сказал один мудрец
Что прежде надо
Связать начало и конец
У численного ряда. Сейчас мы выведем формулу для нахождения суммы n первых членов арифметической прогрессии Пусть сумма первых n членов арифметической прогрессии равна тогда: 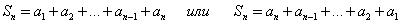
Складывая эти равенства почленно, получим: 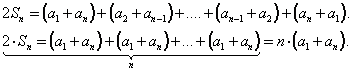
Отсюда имеем формулу: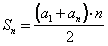 Теорема Сумма первых n членов арифметической прогрессии равна полусумме крайних членов, умноженной на число членов. Если учесть, что 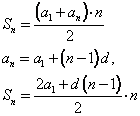 то получим то получим  | Слушают объяснение учителя
Записывают решение задачи в тетрадь
Записывают в тетради тему урока
Слушают объяснение учителя Задают вопросы Записывают в тетради
|
| 6. | Практическая деятельность
| Пример 1 Найдите сумму первых 20 членов арифметической прогрессии: 1; 3,5; … . Дано: Решение: 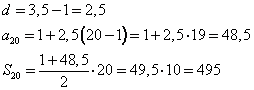
Ответ: 495 Пример 2 Найдите сумму первых 35 членов арифметической прогрессии, если её шестой член равен 31, десятый 55. Дано: Решение: 

Ответ: 3605 Пример 3 Если в арифметической прогрессии первый член равен 20, разность арифметической прогрессии равен (- 0,5) и сумма п-го члена равна 371, то найдём п и ап. Дано: Решение: 

Ответ:  | Один ученик решает у доски Остальные записывают решение в тетрадь
|
| 7. | Практическая деятельность по подготовке к ОГЭ
| Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор. Решение. Пусть бригада в первый день покрасила  метров забора, во второй — метров забора, во второй — 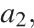 … , в последний — … , в последний —  метров забора. Тогда метров забора. Тогда 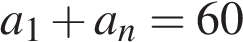 м, а за n дней было покрашено м, а за n дней было покрашено 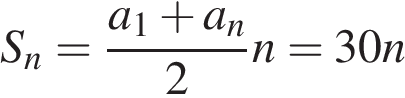 метров забора. метров забора.
Поскольку всего было покрашено 240 метров забора, имеем: 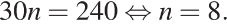 Таким образом, бригада красила забор в течение 8 дней. Таким образом, бригада красила забор в течение 8 дней. Ответ: 8. | Один ученик решает у доски Остальные записывают решение в тетрадь
|
| 7. | Рефлексия деятельности
| Подведем итоги урока: Теперь я умею…. Я научился….. Я считаю, что работал на оценку… | Высказывают своё мнение |
| 8. | Домашнее задание | № 617, № 618 | Записывают задание в дневники, задают вопросы. |









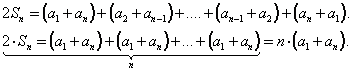
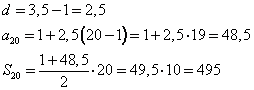




 метров забора, во второй —
метров забора, во второй — 









