Свойства биссектрисы угла

Замечательные точки треугольника Урок 1. Свойство биссектрисы угла

Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является символом геометрии.

Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения - никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника.

А какие треугольники знаете вы?

• Остроугольный, прямоугольный, равнобедренный, равносторонний…

• треугольник египетский,
• треугольник Паскаля,
• треугольник Рёло,
• Бермудский треугольник
• треугольник Пенроуза,

Гиперссылки.

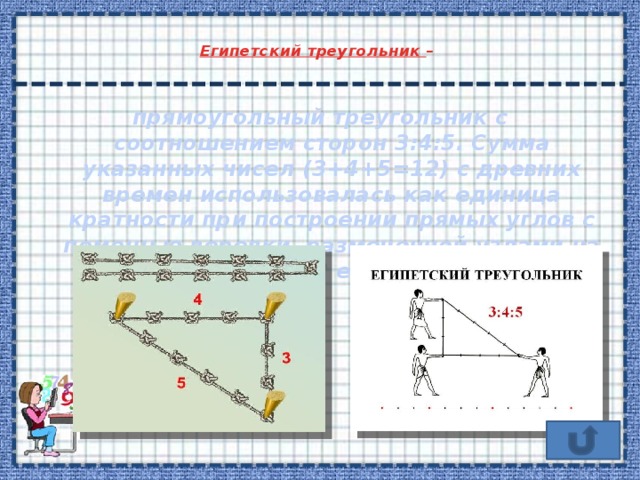
Египетский треугольник –

прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. 

Для возвращения нажмите стрелочку.

Треугольник Паскаля

В этом треугольнике на вершине и по бокам стоят единицы.

Каждое число, которое находится внутри этого треугольника,

равно сумме двух

расположенных

над ним чисел.

Для возвращения нажмите стрелочку.

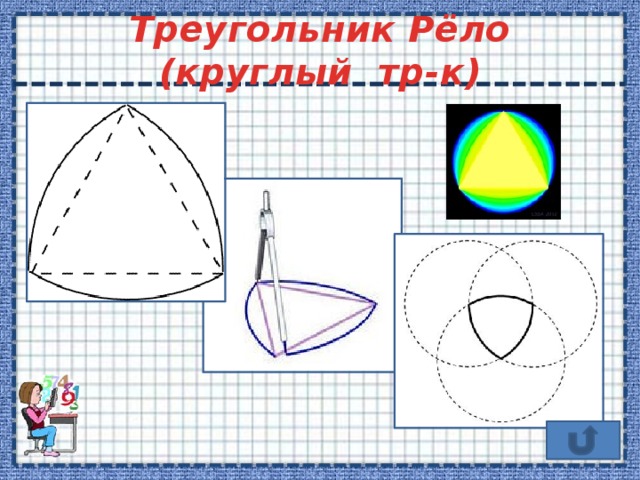
Треугольник Рёло (круглый тр-к)

Для возвращения нажмите стрелочку.

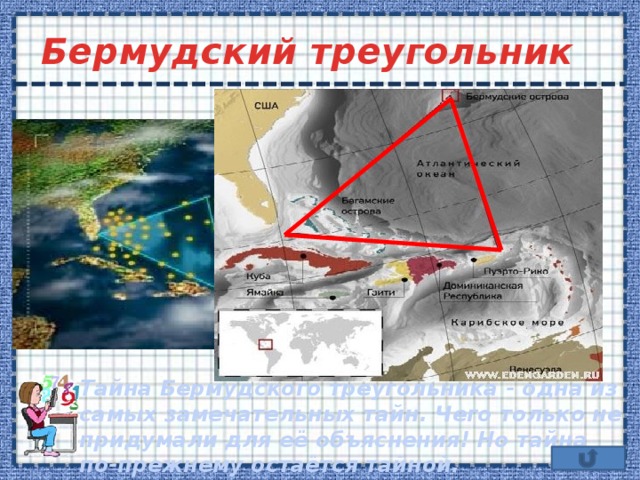
Бермудский треугольник

Тайна Бермудского треугольника - одна из самых замечательных тайн. Чего только не придумали для её объяснения! Но тайна по-прежнему остаётся тайной.

Треугольник Пенроуза

Для возвращения нажмите стрелочку.

Посмотрите внимательно на треугольники –

что вы заметили?

Интересно!

13-метровую скульптуру

треугольника Пенроуза

(невозможного треугольника)

воздвигли в 1999 году в городе

Перт (Австралия).

Но это только вид с этой стороны!

В действительности

"скульптура" выглядит

вот так:

C каждым треугольником связаны четыре точки:

• • точка пересечения медиан;
• • точка пересечения биссектрис;
• • точка пересечения серединных перпендикуляров;
• • точка пересечения высот.

Эти четыре точки называют

замечательными точками треугольника.

Почему они «Замечательные»?

Это нам и предстоит узнать на ближайших уроках.

Свойство биссектрисы

• Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.

Обратно:

• Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.

?

Облачко предполагает вопрос учащимся

12

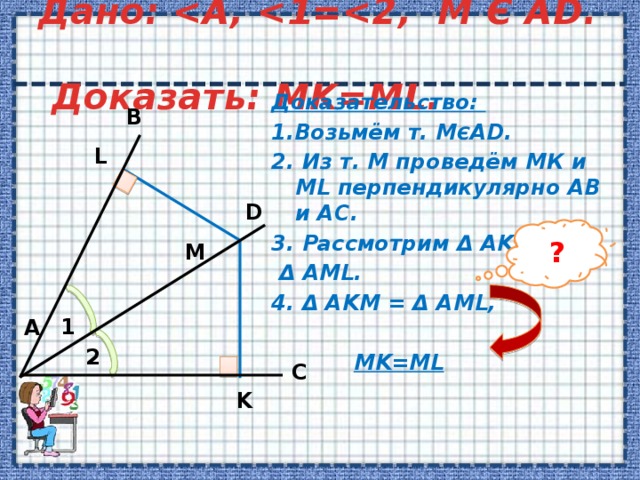
Дано: Доказать: MK=ML.

Доказательство:

1.Возьмём т. М Є AD.

2. Из т. М проведём МК и ML перпендикулярно AB и AC.

3. Рассмотрим Δ AKM и

Δ AML.

4. Δ AKM = Δ AML,

MK=ML

B

L

D

?

M

1

А

2

C

K

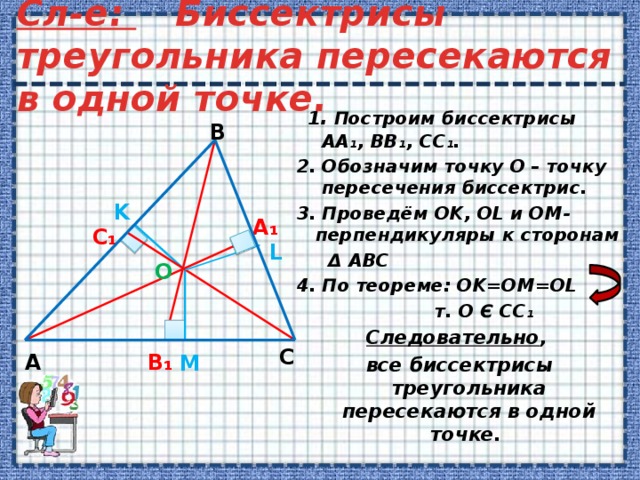
Сл-е: Биссектрисы треугольника пересекаются в одной точке.

1 . Построим биссектрисы АА₁, BB₁, CC₁.

2. Обозначим точку O – точку пересечения биссектрис.

3. Проведём OK, OL и OM-перпендикуляры к сторонам

Δ ABC

4. По теореме: OK=OM=OL

т. О Є СС₁

Следовательно ,

все биссектрисы треугольника пересекаются в одной точке.

В

K

A₁

C₁

L

O

C

A

B₁

M

№ 676 б

• Cтороны угла А, равного 90°, касаются окружности

с центром О и радиусом r, ОА = 14 дм.

Найдите r.

№ 676 б

Решение:

• Проведём радиусы OP и OH из центра окружности в точки касания.
• OP и AP, OH и AH

перпендикулярны

O

H

?

P

A

3. AO – биссектриса угла

4. Δ AOP – прямоугольный.

• По теореме Пифагора:

AO²=OP²+AP²

AO²=r²+r²,

2r²=14², r=7√2.

Ответ: r=7√2дм.

?

№ 678 а- самопроверка

№ 678 а- самостоятельно

В

1) СМ – биссектриса угла С, так как

биссектрисы углов в треугольнике пересекаются в

одной точке

0,5 =0,5·180°-0,5· ( 90°-0,5·(

Дано: ∆АВС, АА 1 и ВВ 1 биссектрисы углов А и В .

Найти:

А₁

C₁

M

С

Решение:

В₁

А

2) ∆АМВ:

3)

Ответ: 46°.

• Что было особенно интересным

и познавательным?

Что нового я узнал

сегодня на уроке?

Домашнее задание:

П.74, с. 187; №№ 676 (а), 678 (б).

Использованные ресурсы:

• Учебник «Геометрия 7-9»; авт: Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. М., Просвещение, 2007г.
• Рисунки треугольников:

Треугольник Рёло:

http://upload.wikimedia.org/wikipedia/commons/c/cf/ReuleauxTriangle.png

http://haritonenko.okis.ru/img/haritonenko/622_4413_1296341088.jpg

http://sibac.info/files/2013_05_07_SchoolNatur/2_Artyushkin.files/image001.jpg

http://commons.wikimedia.org/wiki/File:Mod_Itten_Reuleaux_Triangle_LSSA_256col.gif?uselang=ru

Треугольник Пенроуза:

http://eti.ru/uploads/posts/2011-08/1312994233_glaza11.jpg

http://areeweb.polito.it/didattica/polymath/htmlS/argoment/ParoleMate/Nov_07/Img/Rettangolo.jpg

http://illjuzija.ru/wp-content/uploads/2010/10/skulptura-tryeugolnik-penrouza.jpg

http://illjuzija.ru/wp-content/uploads/2010/10/s-storony-skulptura-tryeugolnik-penrouza-2-e1287403846663.jpg

Треугольник Паскаля:

http://sbirgells.files.wordpress.com/2010/07/pascals_triangle.gif?w=252&h=253

Египетский: http://lib.convdocs.org/pars_docs/refs/252/251618/251618_html_m37e3f8ae.jpg

http://festival.1september.ru/articles/503174/img10.jpg

Использованные ресурсы:

Бермудский треугольник:

http://sobaka.com.ua/c/olds/sobaka/1276506089_0.jpg

http://pirates-life.ru/_fr/9/2824012.jpg

Раскрытая книга :

http://images.funadvice.com/photo/49/photo-book_published_large.jpg

Учебник геометрии: http://www.pomogala.ru/matematika_images/geometry_7_9_atanasyan.JPG

Рисунок треугольника:

http://domsnov.ru/foto/treugolnik.jpg

http://www.clker.com/cliparts/9/a/c/3/11971494591216069200nlyl_orange_triangle.svg.hi.png

Картинка слайда рефлексии:

http://forum.touki.ru/gallery/4d170b90f1d04.png

Тетради:

http://www.orshanka.by/wp-content/uploads/2010/08/Colorful-notebooks-and-pen.jpg

Школьные принадлежности:

http://detsad38.info/metod/img/izonit7.jpg

Знаки вопроса:

http://i.stupenki-studio.ru/u/28/55d73e9aac11e2b7018737826c674f/-/ лог2. jpg

Автор шаблона:

Ермолаева Ирина Алексеевна

учитель информатики и математики МОУ «Павловская сош» с. Павловск Алтайский край