Свойства функции и построение графиков

Функции. Область определения и множество значений, графики. Способы задания функции

Свойства функции

• Область определения
• Множество значений
• Четность- нечетность. Периодичность.
• Координаты точек пересечения с осями координат
• Промежутки знакопостоянства функции.
• Промежутки монотонности (возрастания и убывания) функции
• Точки минимума и максимума. Минимум и максимум функции.

0, xϵ[-3;-2.5) U (1;3] f(x)6. xϵ[-3;-0,5) U (2;3)- функция убывает xϵ(-0,5: 2 )- функция возрастает 7. x min -=-0.5 y min =-2 x max =2 y max =3 " width="640"

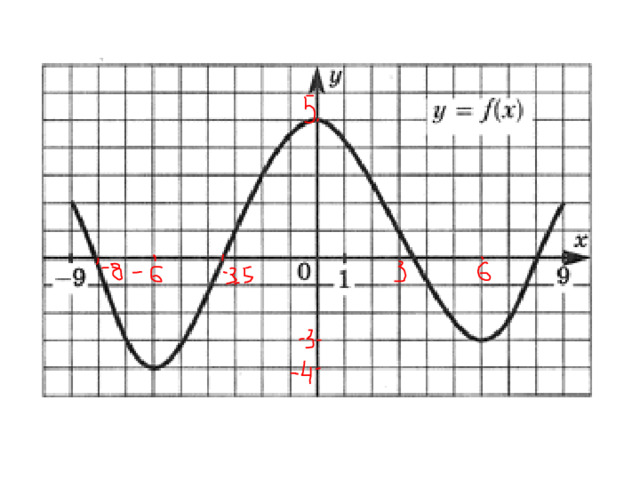
1. Опишите свойства функции по ее графику

• D(y)=[-3;3]
• E(y) =[-2;3]
• Ни четная, ни нечетная. Не периодическая
• Точки пересечения с осями координат: (-2,5;0), (1;0), (0; -1,8)
• f(x)0, xϵ[-3;-2.5) U (1;3]

f(x)

6. xϵ[-3;-0,5) U (2;3)- функция убывает

xϵ(-0,5: 2 )- функция возрастает

7. x min -=-0.5 y min =-2

x max =2 y max =3

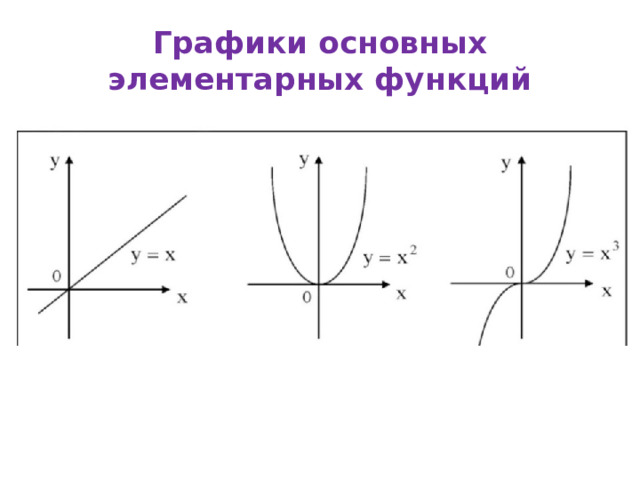
Графики основных элементарных функций

Графики основных элементарных функций

Графики основных элементарных функций

График функции y = sin x

0 при 0 + 2πn  Z sin x  Z 6. промежутки монотонности: x  [- π / 2 + 2πn; π / 2 + 2πn], n  Z – возрастает x  [ π / 2 + 2πn; 3π / 2 + 2πn], n  Z – убывает 7. экстремумы: y max = 1 при х = π / 2 + 2πn, n  Z y min = - 1 при х = - π / 2 + 2πn, n  Z График функции y = sin x " width="640"

Функция y = sin x

Свойства функции:

• D(sin x) = R
• E(sin x) = [- 1 ; 1]

• y = sin x – нечетная функция,

график симметричен относительно

начала координат

периодичность: T = 2π

4. sin x = 0 при х = πn, n  Z (нули функции)

5. промежутки знакопостоянства:

sin x 0 при 0 + 2πn  Z

sin x  Z

6. промежутки монотонности:

x  [- π / 2 + 2πn; π / 2 + 2πn], n  Z – возрастает

x  [ π / 2 + 2πn; 3π / 2 + 2πn], n  Z – убывает

7. экстремумы:

y max = 1 при х = π / 2 + 2πn, n  Z

y min = - 1 при х = - π / 2 + 2πn, n  Z

График функции y = sin x

Построение функции y = sin x ±b

y

y = sin x +1

1

x

y = sin x

0

-3π/2

-π/2

-π

2π

3π/2

π

π/2

-2π

y = sin x -1

-1

Построение функции y = sin x ±b

y

y = sin(x +π/2)

1

x

y = sin x

0

-3π/2

-π/2

-π

2π

3π/2

π

π/2

-2π

y = sin(x -π/2)

-1

Функция y = cos x

0 при - π / 2 + 2πn π / 2 + 2πn, n  Z cos x π / 2 + 2πn 3π / 2 + 2πn, n  Z 6. промежутки монотонности: x  [ π+ 2πn; 2π+ 2πn], n  Z – возрастает x  [0 + 2πn; π+ 2πn], n  Z – убывает 7. экстремумы: y max = 1 при х = 2πn, n  Z y min = - 1 при х = π+ 2πn, n  Z График функции y = cos x " width="640"

Функция y = cos x

Свойства функции:

• D(cos x) = R
• E(cos x) = [- 1 ; 1]

• y = cos x – четная функция,

график симметричен относительно

оси ординат

периодичноть: T = 2π

4. cos x = 0 при х = π / 2 + πn, n  Z ( нули функции )

5. промежутки знакопостоянства:

cos x 0 при - π / 2 + 2πn π / 2 + 2πn, n  Z

cos x π / 2 + 2πn 3π / 2 + 2πn, n  Z

6. промежутки монотонности:

x  [ π+ 2πn; 2π+ 2πn], n  Z – возрастает

x  [0 + 2πn; π+ 2πn], n  Z – убывает

7. экстремумы:

y max = 1 при х = 2πn, n  Z

y min = - 1 при х = π+ 2πn, n  Z

График функции y = cos x

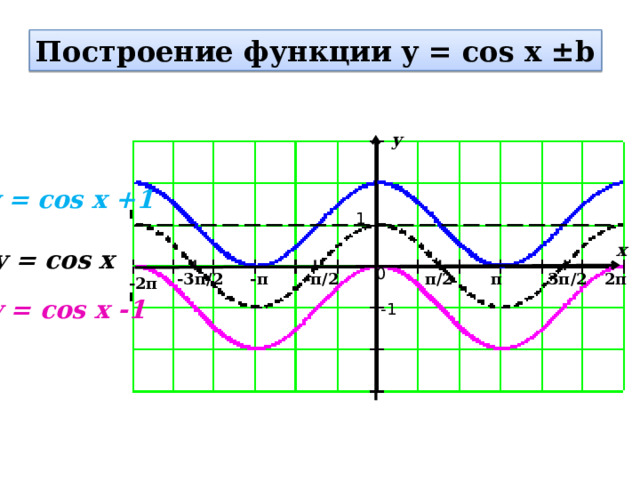
Построение функции y = cos x ±b

y

y = cos x +1

1

x

y = cos x

0

-3π/2

-π/2

-π

2π

3π/2

π

π/2

-2π

y = cos x -1

-1

Построение функции y = cos(x ±π/2)

y

1

y = cos(x -π/2)

x

y = cos x

0

π/2

π

3π/2

2π

-π

-3π/2

-π/2

-2π

y = cos(x +π/2)

-1

График функции y = tg x

0 при 0 + πn π / 2 + πn, n  Z tg x π / 2 + πn  Z 6. промежутки монотонности: x  (- π / 2 + πn; π / 2 + πn), n  Z – возрастает экстремумов нет График функции y = tg x " width="640"

Функция y = tg x

Свойства функции:

• D(tg x) = x  R/ π / 2 + πn, n  Z
• E(tg x) = R

• y = tg x – нечетная функция

график симметричен относительно

начала координат

3. периодичность: T = π

4. tg x = 0 при х = πn, n  Z ( нули функции )

5. промежутки знакопостоянства:

tg x 0 при 0 + πn π / 2 + πn, n  Z

tg x π / 2 + πn  Z

6. промежутки монотонности:

x  (- π / 2 + πn; π / 2 + πn), n  Z – возрастает

• экстремумов нет

График функции y = tg x

График функции y = ctg x

0 при 0 + πn π / 2 + πn, n  Z ctg x π / 2 + πn  Z 6. промежутки монотонности: x  (0+ πn; π+ πn), n  Z – убывает экстремумов нет График функции y = ctg x " width="640"

Функция y = ctg x

Свойства функции:

• D(ctg x) = (0+πn; π+πn), n  Z
• E(ctg x) = (-∞; +∞)

• y = ctg x – нечетная функция

график симметричен относительно

начала координат

3. периодичноть: T = π

4. ctg x = 0 при х = π / 2 + πn, n  Z ( нули функции )

5. промежутки знакопостоянства:

c tg x 0 при 0 + πn π / 2 + πn, n  Z

ctg x π / 2 + πn  Z

6. промежутки монотонности:

x  (0+ πn; π+ πn), n  Z – убывает

• экстремумов нет

График функции y = ctg x