Просмотр содержимого документа
«Свойства параллелограмма.»
| Школа-Гимназия №6 |
| Свойства параллелограмма |
| Обобщающий урок |
| геометрия 8 класс
|
|
|
|
|
|
|
| ![]()
|
| . |
|
|
Урок учителя по математике
школы-гимназии №6
Германцевой Гульфиры Равильевны.
Геометрия, 8 класс
Обобщающий урок по геометрии по теме «Свойства параллелограмма.
Цели:
1. Обобщить и расширить знания по изученному материалу, отработать навыки решения типовых задач.
2. Развивать у учащихся математическую речь, формировать умения систематизировать и обобщать полученные знания, развивать навык использования знаний на практике.
Воспитание осмысленной учебной деятельности, развитие положительных мотивов в учебно-познавательной деятельности.
Оборудование: Опорные схемы – «Четырёхугольники» и «Свойства параллелограмма» и «Диаграмма Эйлера», комплекты разноцветных моделей всех видов параллелограммов на каждого ученика, тесты в двух вариантов на каждого ученика, макет фундамента дома, кусок материи, домашняя контрольная работа в двух вариантах на каждого ученика.
Ход урока:
Организационный момент.
Вступительное слово учителя: Сегодня мы завершаем тему «Свойства параллелограмма». Целью нашего урока является закрепление и систематизация материала по данной теме, а также применение полученных знаний в практической деятельности человека.
Фронтальное обсуждение опорных схем.
Обсуждение опорной схемы «Четырёхугольники».
На доске:

Вопросы учителя и примерное изложение ответов учащихся:
| Вопросы: | Ответы: |
Как называется самая верхняя фигура? | Это четырёхугольник – фигура, состоящая из четырёх точек, соединённых между собой отрезками. |
Почему четырёхугольник изображен странным: у него нет равных сторон и углов? | Потому, что в определении не сказано ничего о равенстве сторон или углов, о параллельности сторон. Можно изобразить любую фигуру с четырьмя сторонами, лишь бы она была выпуклой. |
О чём говорят стрелки, проведённые от верхнего четырёхугольника? | Стрелки показывают, что из всех четырёхугольников можно выделить «особые», которые имеют больше характерных признаков, чем остальные. |
Какие «особые» четырёхугольники можно выделить? | Это параллелограммы и трапеции. Учениками даются определения данных фигур. |
Существуют ли разновидности параллелограммов и трапеций? | Да. У параллелограммов это ромбы, прямоугольники и квадраты. У трапеций - это с прямыми углами и двумя равными сторонами. |
Дайте определения ромба, прямоугольника и квадрата. | Даются определения, данные в учебнике. |
Методический комментарий. В ходе беседы учащиеся вспомнили свойства изучаемых фигур, получили представление о логическом приёме классификации. Для них необходимо понять, что выделяемые множества объектов зависят от того, какой признак взят за основу классификации. Так как речь идёт о включении одного множества в другое, то полезно составить диаграмму, изображающую четырёхугольники и его виды.
Обсуждение опорной схемы «Диаграмма Эйлера».
На доске:

По диаграмме Эйлера объяснить учащимся о включении одного множества в другое. Таким образом даются поредставления о понятиях «классификация», «множество», «включение».
Обсуждение опорной схемы 2 «Свойства параллелограмма и его разновидностей».
На доске:



1
180°
2




Свойства квадрата
Вопросы учителя и примерное изложение ответов учащихся:
| Вопросы: | Ответы: |
О каком свойстве параллелограмма можно говорить по рис.1? | В параллелограмме противоположные стороны равны. |
Как можно прокомментировать рис.2? | В параллелограмме противоположные углы равны. |
Почему на рис.3 сделана надпись: «1800»? | Сумма углов, принадлежащих одной стороне параллелограмма, равна 1800. |
Как прокомментировать рис.4? | Диагонали параллелограмма делятся точкой пересечения пополам. |
О каком свойстве параллелограмма можно говорить по рис.5? | Диагональ делит параллелограмм на два равных треугольника. |
Обладает ли ромб свойствами параллелограмма? | Да, всеми свойствами, показанными на рис.1-5, так как ромб - это параллелограмм. |
Если у ромба отличительные свойства? | Да, на рис.6. У ромба диагонали пересекаются под прямым углом. На рис.7. Диагонали ромба являются биссектрисами его углов. |
Обладает ли прямоугольник свойствами параллелограмма? | Прямоугольник обладает всеми свойствами параллелограмма. |
Обладает ли прямоугольник свойствами ромба? | Нет, прямоугольник не обладает свойствами ромба. |
Каким отличительным свойством обладает прямоугольник? | В прямоугольнике диагонали равны и все углы прямые. |
Какая фигура называется квадратом? | Можно дать два определения. Квадрат - это прямоугольник, у которого все стороны равны или это ромб, у которого углы прямые. |
Какую фигуру можно выделить особо по количеству свойств? | Это квадрат. Он обладает всеми свойствами перечисленных фигур. |
Закрепление материала.
У каждого ученика на парте лежат разноцветные модели ромба, прямоугольника, квадрата и параллелограмма. По просьбе учителя ученики поднимают ту фигуру или фигуры, которые обладают названным свойством.
| Свойства: | Модели: |
Имеет равные диагонали. | Прямоугольник, квадрат. |
Имеет равные противоположные углы. |
Все модели. |
Имеет перпендикулярные диагонали. |
Ромб, квадрат. |
Имеет равные противоположные стороны. |
Все модели. |
Углы, прилежащие одной стороне в сумме составляют 1800. |
Все модели. |
Диагонали являются биссектрисами его углов. |
Ромб, квадрат. |
Сумма всех углов равна 3600 | Все модели. |
Все углы прямые. | Прямоугольник, квадрат. |
Диагонали делятся точкой пересечения пополам. |
Все модели. |
Противоположные стороны лежат на параллельных прямых. |
Все модели. |
Все стороны равны. | Ромб, квадрат. |
Диагонали делят фигуру на четыре равных треугольника. |
Ромб, квадрат. |
Опрос учащихся.
Опрос происходит в виде теста, представленного на листочках, которые выдаёт учитель.
Задания в тесте:
Если диагонали у параллелограмма равны, то он может быть:
Только квадратом;
Квадратом или прямоугольником;
Только прямоугольником;
Любым четырёхугольником.
Если у параллелограмма диагонали пересекаются под прямым углом, то он может быть:
Только ромбом;
Ромбом или квадратом;
Любым прямоугольником.
Чему равна сумма углов параллелограмма:
1800 ;
900 ;
3600 ;
7200 ?
Если одна сторона параллелограмма равна 10 см, а другая сторона 20 см, то периметр равен:
10 см;
20 см;
120 см;
60 см.
Если стороны параллелограмма 3 и 5 см, то какие эти стороны:
Соседние;
Противоположные;
Любые?
Если один угол параллелограмма равен 420 , то чему равны другие его углы:
420 и 820;
420, 840, 540;
420, 1380, 1380;
840 и 1380?
Сумма двух углов параллелограмма равна 1000. Какие это углы:
Соседние;
Противоположные;
Любые?
Если диагональ параллелограмма образует с его сторонами углы 300 и 400 то углы параллелограмма равны:
600 и 800;
700 и 100;
700 и 1100.
Код правильного ответа: 1 - B; 2 – В; 3 – C; 4 - D; 5 – A; 6 – C; 7 – B; 8 – C.
Окончив работу, ученики сдают листочки с ответами. Открывается код теста.
Применение полученных знаний в практической деятельности.
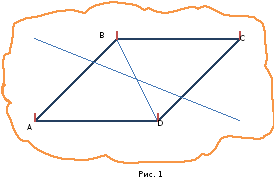
Задача №1. Чтобы наметить на местности фундамент дома прямоугольной формы, поступили так: с помощью мерных веревок отметили колышками точки A, B, C, и D так, чтобы AB=CD, BC=AD (рис.1). Далее произвели проверку. Для этого натянули мерную веревку сначала между вершинами A и С, а потом между вершинами B и D. Убедившись, что AC=BD, сделали вывод, что ABCD - прямоугольник. Правильно ли?
Задача №2. Четырехугольный кусок материи перегнули по одной диагонали и убедились в точном совмещении двух образовавшихся в результате треугольников (рис. 2). Затем материю развернули, перегнули по другой диагонали и снова убедились в совмещении треугольников.
Можно ли гарантировать, что кусок материи имеет форму квадрата?
Итоги урока. На уроке мы закрепили и систематизировали изученный материал по теме «Свойства параллелограмма», а также нашли применение этим свойствам в практической деятельности человека.
Домашнее задание: Домашняя контрольная работа в двух вариантах.
1 вариант.
В параллелограмме ABCD АЕ – биссектриса угла BAD. Точка Е лежит на стороне BC. AB =7 см, EC = 3 см . Найдите периметр ABCD.
Докажите, что четырёхугольник, у которого две стороны параллельны и углы, прилежащие к одной из этих сторон прямые, является прямоугольником.
2 вариант.
В параллелограмме ABCD BЕ – биссектриса угла ABC. Точка Е лежит на стороне AD. AE=8 см, ED=2 см. Найдите периметр ABCD.
Докажите, что четырёхугольник, у которого все стороны равны, является ромбом.