Свойства равнобедренного треугольника

ГЕОМЕТРИЯ 7 класс

Тема: Свойства равнобедренного треугольника.

Цели:

изучить свойства равнобедренного треугольника, закрепить знание свойств равнобедренного треугольника при решении задач;

развивать логическое мышление и геометрическую зоркость учащихся, развивать познавательный интерес к предмету, мышление, внимание, память;

воспитывать настойчивость в учебе, умение слушать, ответственное отношение к учебному труду, самостоятельность.

Ход урока.

I. Оргмомент.

На уроках геометрии очень важно уметь, смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.

Кто ничего не замечает,

Тот ничего не изучает.

Кто ничего не изучает,

Тот вечно хнычет и скучает.

Сегодня мы на уроке постараемся не хныкать и не скучать, а как можно больше замечать, видеть и делать выводы.

II. Актуализация знаний.

1. Дайте определение треугольника.

2. Сформулируйте первый признак равенства треугольников.

3. Что называется периметром треугольника?

4. Работа по готовым чертежам: из следующих треугольников выберите равные. Ответ обоснуйте.

– Какой треугольник выделяется из общего фона? В чем его особенность? (у него есть пара равных сторон).

III. Сообщение темы и целей урока.

– Сегодня на уроке мы будем рассматривать именно такие треугольники. Откройте учебники и найдите название треугольника, у которого две стороны равны. Как называются такие треугольники? (равнобедренные)

– Именно так звучит тема нашего сегодняшнего урока. Запишите в тетрадях тему урока.

– Какие цели мы поставим перед собой на уроке? (Ученики сам формулируют цели урока).

IV. Изучение нового материала.

1. Понятие равнобедренного треугольника.

– Сегодня на уроке мы познакомимся с конкретным видом треугольника – равнобедренным треугольником. Давайте начертим такой треугольник, т.е. треугольник, у которого две стороны равны.

В АВ = ВС – боковые стороны равнобедренного треугольника;

АС – основание равнобедренного треугольника.

А С

– Если говорят, что треугольник АВС равнобедренный с основанием АС, то это значит, что две другие стороны АВ и ВС – боковые, т.е. АВ = ВС.

2. Устная работа по готовым чертежам.

– Какие треугольники на рисунке являются равнобедренными, почему? У равнобедренных треугольников назовите

– боковые стороны;

– основание;

– угол, противолежащий основанию;

– углы, прилежащие к основанию.

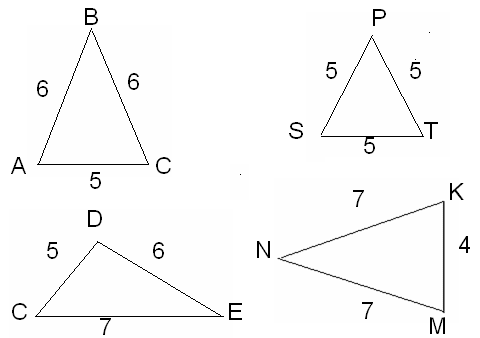
– Что можно сказать о треугольнике SPT? Является ли он равнобедренным? Тогда какую сторону можно рассмотреть как основание, и какие стороны будут боковыми?

ОПРЕДЕЛЕНИЕ: треугольник, у которого все стороны равны, называется равносторонним.

3. Свойства равнобедренного треугольника.

– Докажем свойства равнобедренного треугольника.

• ЗАДАНИЕ 1. (у доски 1 ученик, остальные выполняют работу в тетрадях)

– Начертите равнобедренный треугольник АВС с основанием АС.

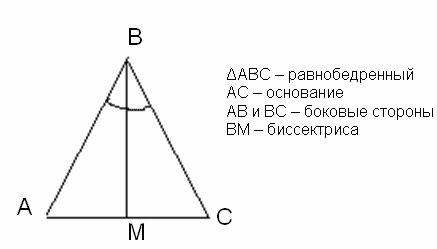
– Проведите биссектрису угла при вершине В. Назовите её ВМ.

– На сколько треугольников разбила биссектриса ВМ треугольник АВС? (на два)

– Что мы можем сказать об углах АВМ и СВМ? (они равны)

– А какими между собой являются треугольники АВМ и СВМ? (равными)

– Докажите, что эти треугольники равны.

АВ = ВС по условию,

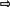∟АВМ = ∟СВМ, т.к. ВМ – биссектриса, ∆АВМ = ∆СВМ по двум сторонам и углу меж-

ВМ – общая сторона ду ними.

– Что дает нам доказанное равенство треугольников АВМ и СВМ? (из равенства треугольников следует равенство все его элементов)

– А какие элементы равны? (∟А = ∟С)

– А в равнобедренном треугольнике АВС это какие углы? (углы при основании)

– Мы доказали одно из свойств равнобедренного треугольника: в равнобедренном треугольнике углы при основании равны.

• ЗАДАНИЕ ПО РИСУНКАМ. Найдите градусную меру неизвестных углов.

– Какое свойство мы использовали при решении задач?(свойство углов при основании равнобедренного треугольника)

– А какие еще пары равных элементов дает равенство треугольников АВМ и СВМ? (АМ = СМ)

– Т.е. отрезок ВМ соединяет вершину Вв треугольнике АВС с серединой противоположной стороны АС. А значит, чем является отрезок ВМ? (медианой)

– ВЫВОД: значит, в равнобедренном треугольнике биссектриса, проведенная к основанию является ещё и медианой.

– И последняя пара равных элементов, которую вы ещё не назвали? (∟АМВ= ∟СМВ)

– Какие углы они образуют? (смежные, их сумма равна 180⁰, а т.к. они равны, то каждый из них по 90⁰)

– В таком случае отрезок ВМ чем еще является? (высотой)

– Таким образом мы доказали еще одно свойство равнобедренного треугольника (ученики читают его в учебнике)

– А если провести биссектрису угла А к боковой стороне ВС. Является ли в этом случае биссектриса АD и медианой, и высотой? (нет) (продемонстрировать на рисунке)

– А в каком треугольнике любая биссектриса будет и медианой, и высотой? (в равностороннем – продемонстрировать с помощью программы «Живая математика»)

– Мы установили, что биссектриса, медиана и высота равнобедренного треугольника, проведенные к основанию, совпадают. Поэтому справедливы также утверждения:

1.Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

2.Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

V. Закрепление изученного.

1. Задача 1. (работа в группах)

Дано:∆ АВС – равнобедренный, АС – основание, ВК – биссектриса, АС = 46 см.

Найти: АК.

2. Задача 2. (работа в группах)

DA – медиана равнобедренного ∆ ВDС, проведенная к основанию СВ. Найдите углы ∆ АDС ,

если ∟BDC = 120˚, ∟DBC = 30⁰.

3. №112 (если останется время)

VI.Итоги урока.

• Какой треугольник называется равнобедренным?

• Какой треугольник называется равносторонним?

• Является ли равносторонний треугольник равнобедренным?

• Каким свойством обладают углы равнобедренного треугольника?

• Каким свойством обладает биссектриса равнобедренного треугольника?

• Любая ли биссектриса обладает этим свойством? Какая?

• Любая ли биссектриса равностороннего треугольника обладает этим свойством?

VII. Задание на дом: п. 18, №107, 111, творческое задание: из четырех спичек сделать 4 равносторонних треугольника.