Свойства равнобедренного треугольника

Свойства равнобедренного и равностороннего треугольника

Работу выполнила Согласнова Анастасия 9» Б»

История появления

Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, т. к. эта фигура всегда имела широкое применение в практической жизни.Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта.. Еще в древности стали вводить некоторые знаки обозначения для геометрических фигур.Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник.Прямоугольный треугольник занимал почетное место в Вавилонской геометрии. Стороны прямоугольного треугольника: гипотенуза и катеты

Термин «гипотенуза» происходит от греческого слова «ипонейноуза», обозначающее «тянущаяся над чем-либо», «стягивающая». Слово берет начало от образа древнегреческих арф, на которых струны натягиваются на концах двух взаимно-перпендикулярных подставок. Термин «катет» происходит от греческого слова «катетос», которое означает начало «отвес», «перпендикуляр».Евклид говорил: «Катеты – это стороны, заключающие прямой угол».В Древней Греции уже был известен способ построения прямоугольного треугольника на местности. Для этого использовали веревку, на которой были завязаны 13 узелков, на одинаковом расстоянии друг от друга. Давайте и мы попробуем построить прямоугольный треугольник.

Свойства равнобедренного треугольника

• 1) В равнобедренном треугольнике  углы при основании  равны.
• 2) В равнобедренном треугольнике
• —  медиана ,
• —  биссектриса
• — и  высота , проведенные к основанию, совпадают.
• Например,
• если в треугольнике ABC AC=BC, то:
•  ∠ A=∠B
• CF — высота, медиана и биссектриса,
• то есть, ∠AFC=90º,
• AF=BF,
• ∠ ACF=∠BCF.
• Треугольники ACF и BCF — равные прямоугольные треугольники.
•  

3) В равнобедренном треугольнике

• —  биссектрисы, проведенные из вершин при основании , равны;
• —  высоты, проведенные из вершин при основании , равны;
• —  медианы, проведенные из вершин при основании , равны.
•  

Треугольник является равнобедренным, если у него присутствуют следующие  признаки :

1.  Два угла у треугольника равны.

2.  Высота является медианой.

3.  Биссектриса является медианой.

4.  Высота является биссектрисой.

5.  Две высоты треугольника равны.

6.  Две биссектрисы треугольника равны.

7.  Две медианы треугольника равны.

Задача 1

Пусть дан равнобедренный треугольник АВС  (рис. 1) .

1) Так как АС : ВС = 6 : 5, то АС = 6х и ВС = 5х. ВН – высота, проведенная к основанию АС треугольника АВС.

Так как точка Н – середина АС (по свойству равнобедренного треугольника), то НС = 1/2 АС = 1/2 · 6х = 3х.

2) Из треугольника ВНС – прямоугольного по теореме Пифагора

ВС 2  = ВН 2  + НС 2 ;

(5х) 2  = 8 2  + (3х) 2 ;

16х 2  = 64;

х 2  = 4;

х = 2, тогда

АС = 6х = 6 · 2 = 12 и

ВС = 5х = 5 · 2 = 10.

3) Так как точка пересечения биссектрис треугольника является центром вписанной в него окружности, то ОН = r . Радиус вписанной в треугольник АВС окружности найдем по формуле

S = pr;

r = S/p.

4) S ABC  = 1/2 · (AC · BH); S ABC  = 1/2 · (12 · 8) = 48;

p = 1/2 · (AB + BC + AC); p = 1/2 · (10 + 10 + 12) = 16, тогда ОН = r = 48/16 = 3.

Отсюда ВО = ВН – ОН; ВО = 8 – 3 = 5.

Ответ: 5.

Задача 2

В равнобедренном треугольнике АВС проведена биссектриса АD. Площади треугольников ABD и ADC равны 10 и 12. Найти увеличенную в три раза площадь квадрата, построенного на высоте этого треугольника, проведенной к основанию АС.

Решение.

Рассмотрим треугольник АВС – равнобедренный, АD – биссектриса угла А  (рис. 2).

1) Распишем площади треугольников ВАD и DAC:

S BAD  = 1/2 · AB · AD · sin α; S DAC  = 1/2 · AC · AD · sin α.

2) Найдем отношение площадей:

S BAD /S DAC  = (1/2 · AB · AD · sin α) / (1/2 · AC · AD · sin α) = AB/AC.

Так как S BAD  = 10, S DAC  = 12, то 10/12 = АВ/АС;

АВ/АС = 5/6, тогда пусть АВ = 5х и АС = 6х.

АН = 1/2 АС = 1/2 · 6х = 3х.

3) Из треугольника АВН – прямоугольного по теореме Пифагора АВ 2  = АН 2  + ВН 2 ;

25х 2  = ВН 2  + 9х 2 ;

ВН = 4х.

4) S AВС  = 1/2 · AС · ВН; S AВC  = 1/2 · 6х · 4х = 12х 2 .

Так как S AВС  = S BAD  + S DAC  = 10 + 12 = 22, тогда 22 = 12х 2 ;

х 2  = 11/6; ВН 2  = 16х 2  = 16 · 11/6 = 1/3 · 8 · 11 = 88/3.

5) Площадь квадрата равна ВН 2  = 88/3; 3 · 88/3 = 88.

Ответ: 88

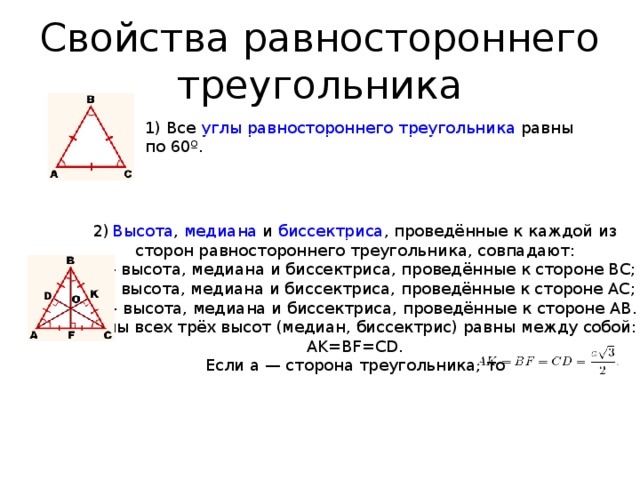
Свойства равностороннего треугольника

1) Все  углы равностороннего треугольника  равны по 60º.

2)   Высота ,  медиана  и  биссектриса , проведённые к каждой из сторон равностороннего треугольника, совпадают:

AK — высота, медиана и биссектриса, проведённые к стороне BC;

BF — высота, медиана и биссектриса, проведённые к стороне AC;

CD — высота, медиана и биссектриса, проведённые к стороне AB.

Длины всех трёх высот (медиан, биссектрис) равны между собой:

AK=BF=CD.

Если a — сторона треугольника, то

3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).

4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:

AO:OK=BO:OF=CO:OD=2:1.

5) Расстояние от точки пересечения высот, биссектрис и медиан

до любой вершины треугольника равно радиусу  описанной окружности :

BO=R,

или

6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу  вписанной окружности :

OF=r,

или

7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.

8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности:

R=2r.