Здравствуйте ребята!
Садитесь.
У вас на партах лежат рабочие листы, запишите на них дату в правом верхнем углу.
Ребята, как вы считаете, где в жизни используется математика? А геометрия?
ответы детей
(возможные предположения)
+++++ 1. Если дети ответят в архитектуре, то я говорю……
Говоря об архитектуре, математику используют по нескольким причинам. Даже если отбросить необходимость математики для проектирования здания, архитекторы используют геометрию для определения пространственной формы здания.
- - - - - 2. Если дети не ответят, то я говорю……
Ко всему перечисленному также можно добавить архитектуру, в которой математику используют по нескольким причинам. Даже если отбросить необходимость математики для проектирования здания, архитекторы используют геометрию для определения пространственной формы здания.
Я предлагаю вам вспомнить о Пизанской башне.
Слайд (с башней)
Пиза́нская башня
(итал. Torre pendente di Pisa) — колокольная башня, часть ансамбля городского собора Санта-Мария-Ассунта (Пизанский собор) в городе Пиза, получившая всемирную известность благодаря непреднамеренному наклону.
-
Основные сведения: Башня имеет 294 ступеньки. Высота башни составляет 55,86 м от земли в самой низкой точке и 56,7 м в самой высокой точке. Диаметр основания — 15,54 м. Автор проекта Бонанно Пизано. Строительство башни велось в 2 этапа, начиная с 9 августа 1173, и с двумя длинными перерывами продолжалось почти 200 лет, до 1360 года.
Что же послужило причиной наклона башни?
ответы детей
(возможные предположения)
Оказывается, изначально ошибка была еще в самом начале проектирования башни. Фундамент, который заложен, не соответствовал высоте и толщине стен.
Ребята, как вы думаете, от чего зависит прочность здания?
Ответы детей
(фундамент)
Ребята, а какую форму фундамента имеют здания, в которых мы живем и учимся?
Ответы детей
(прямоугольную форму)
Да, в основе фундамента наших зданий прямоугольник.
Чтобы построить прочное здание, надо заложить прочный фундамент.
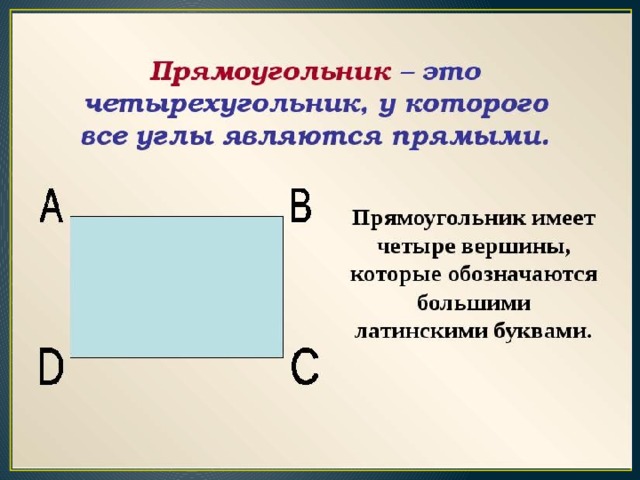
Итак, вот прямоугольник. Прямоугольник – это четырехугольник, у которого все углы прямые.
Слайд (прямоугольник)
Давайте вспомним, что мы знаем о прямоугольнике?
Ответы детей
(периметр, площадь, диагональ, стороны)
Проверим наши ответы
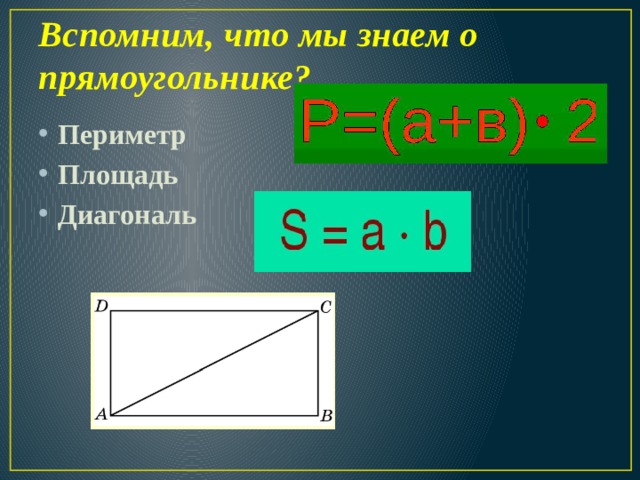
Слайд (формулы)
1) Периметр (+формула)
2) Площадь (+формула)
3) Диагональ
4) Стороны противолежащие (параллельные)
Я предлагаю вам, на рабочих листах под номером 1 начертить прямоугольник, как на картинке с вершинами A, B, C, D и диагональю AC.
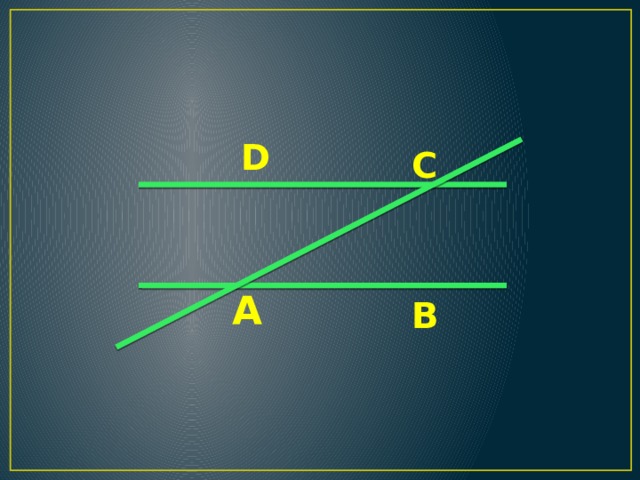
А давайте продолжим противолежащие стороны AB и DC, и диагональ AC.
А стороны AD и СB сотрем.
Что мы с вами получили?
ответы детей
(две параллельные прямые, которые пересекает секущая)
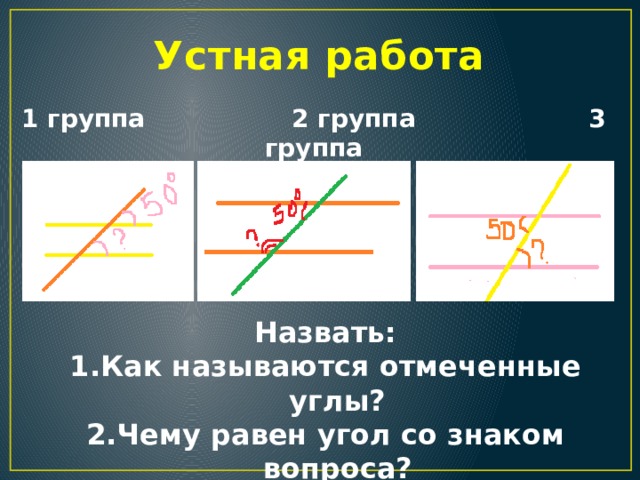
А давайте вспомним, что мы уже выучили по данной теме. Для этого я предлагаю вам решить устно задачи на картинках.
Ваша задача сказать, как называются отмеченные углы, и чему равен угол со знаком вопроса.
Работать будем по рядам, 1-й ряд – 1-я картинка, 2-й ряд – 2-я картинка и соответственно 3-й ряд – 3-я картинка.
Итак, первый ряд, кто готов отвечать?
ответы детей
(1 картинка – соответственные углы, 50 градусов
2 картинка – внутренние односторонние углы, 130 градусов
3 картинка – внутренние накрест лежащие углы, 50 градусов)
Виды углов повторили, теперь давайте повторим признак параллельности прямых. Желающие
ответы детей
(п.31 признак параллельности прямых:
Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180 градусов, то прямые параллельны, т.4.2)
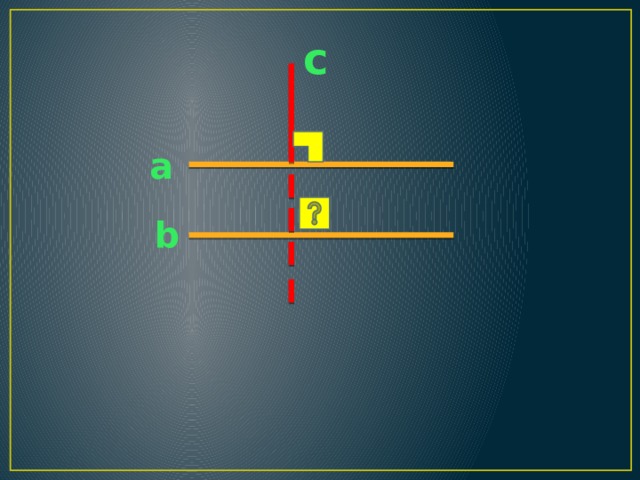
А если секущая по отношению к одной из прямых проходит под прямым углом, то чему будут равны остальные углы?
слайд (прямой угол)
ответы детей
(все углы прямые)
Итак, давайте сделаем вывод
слайд (вывод)
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180 градусов.
Т.О. мы пришли с вами к свойству, которым обладают углы, образованные при пересечении параллельных прямых секущей.
Поэтому на рабочих листах сверху, в отведенном для темы месте вписываем тему нашего урока
слайд (тема урока)
«Свойства углов, образованных при пересечении параллельных прямых секущей»
Прежде чем перейти к решению задач, давайте проведем физкульминутку.
слайд (физкультминутка)
Для этого встанем.
Ученик читает задания для физкультминутки
1.Сожмите кисть столько раз, сколько равна площадь прямоугольника со сторонами 3см, 2 см. Ответ: 6 раз.
2. а=2см, в=1см
Наклоны туловищем влево/вправо столько раз, сколько равен периметр прямоугольника. Ответ: 6 раз
3. Присядьте столько раз, сколько будет равна площадь квадрата со стороной 1см.
Ответ: 1
Немножко отдохнули, переходим к решению задач.
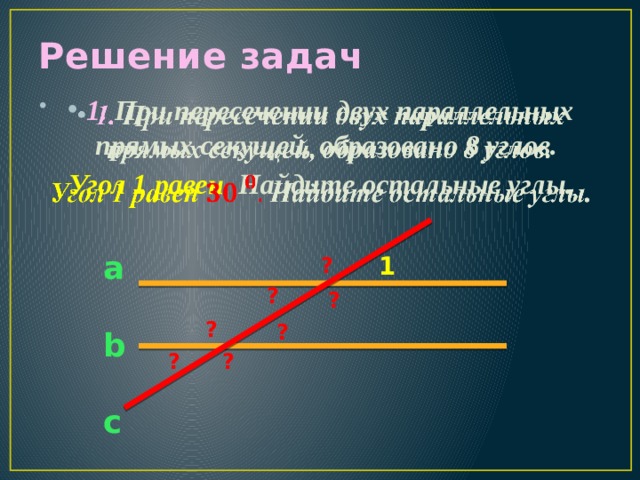
Слайд ЗАДАЧА 1
1. При пересечении двух параллельных прямых секущей, образовано 8 углов. Угол 1 равен 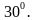 Найдите остальные углы.
Найдите остальные углы.
Решение
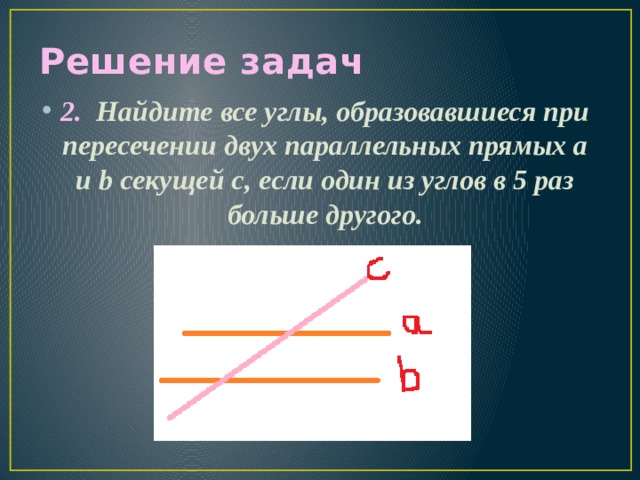
Слайд ЗАДАЧА 2
2. Найдите все углы, образовавшиеся при пересечении двух параллельных прямых а и b секущей c, если один из углов в 5 раз больше другого.
Решение
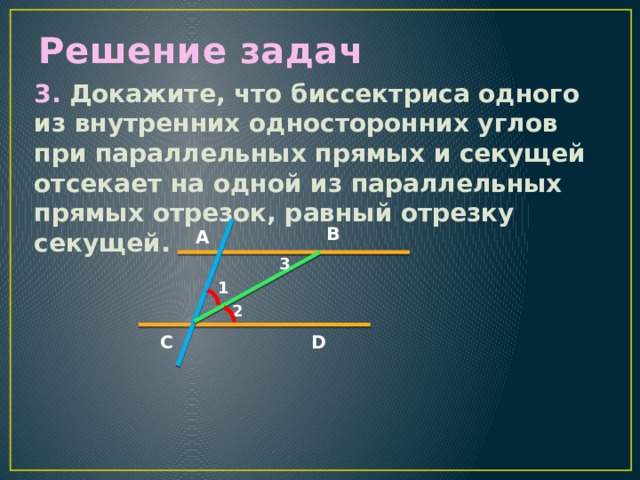
Слайд ЗАДАЧА 3 (резерв)
3. Докажите, что биссектриса одного из внутренних односторонних углов при параллельных прямых и секущей отсекает на одной из параллельных прямых отрезок, равный отрезку секущей.
Дано
Доказать
Доказательство
Теперь давайте проработаем эту тему в игровой форме, 1 человек с ряда читает предложение, а весь ряд говорит верно/неверно (такое задание вы встретите в государственной итоговой аттестации). Записывайте номера верных утверждений в рабочие листы под номером 4.
слайд (ИГРА ВЕРНО/НЕВЕРНО)
-
Две прямые на плоскости называются параллельными, если они не пересекаются.
-
При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.
-
Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
-
Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
-
Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
6. Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
Прежде чем подвести итоги, запишите домашнее задание на своих рабочих листах.
слайд ДОМАШНЕЕ ЗАДАНИЕ
Итак, давайте подведем итог. У каждого из вас на рабочем листе внизу записаны фразы, касающиеся нашей темы, но в них пропущено несколько слов, ваша задача их правильно вписать. Приступайте к выполнению.
ответы детей
Давайте проверим
Слайд (по очереди высвечивать ответ)
-
Две прямые на плоскости называются параллельными, если они не пересекаются.
-
Через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.
-
Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
-
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°. (теорема 4.3)
Молодцы!
СЛАЙД НА УРОКЕ Я…………
Теперь возьмите вот такие листочки и продолжите каждую фразу на уроке я…
По желанию листочки подпишите. Кто написал, передаем мне.
слайд (башня и смайлики)
Так как хорошее настроение одна из главных составляющих успеха, поэтому давайте на смайликах, которые лежат у вас на партах, дорисуем свое настроение, и этим настроением укрепим нашу башню!
Предлагаю каждому из Вас приклеить свой смайлик на фото Пизанской башни.
Ввиду имеющегося наклона высота южной и северной стороны здания неодинаковы. Так, с наклонной стороны (северной) она равна 55,8 м, а с противоположной составляет 56,6 м.
слайд (спасибо за урок)
Спасибо за урок!
Спасибо за внимание!
Опыт Галилео
Любопытно, что история этого сооружения связана с именем великого астронома, математика и физика XVII века Галилео Галилея, родившегося в Пизе в 1642 году. Поскольку Пизанская башня наклонена в сторону, она явилась весьма удобным местом для проведения его опытов. Именно Галилей сбрасывал предметы разной массы, иллюстрируя ученикам свои научные выводы. Несмотря на то, что в прежние годы ряд исследователей подвергал эту информацию сомнению, позднейшие открытия показали её достоверность. Все тела при падении движутся одинаково: начав падать одновременно, они движутся с одинаковой скоростью. Движение происходит с постоянным ускорением.






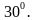 Найдите остальные углы.
Найдите остальные углы.