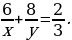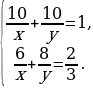| I. Организационный момент | Приветствие. Проверка готовности обучающихся к уроку. Создание в классе атмосферы психологического комфорта. – Предлагаю в начале урока обратить внимание на высказывание: «Математику уже затем учить надо, что она ум в порядок приводит» (М.Ломоносов). – Что скажете? Согласны? | Настраиваются на учебную деятельность. Концентрируют внимание на работе на уроке.
| Формирование навыков самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает обучающимся определить, какие ассоциации у них вызывают слова «математическое моделирование».
Вопрос запуска постановки учебной задачи: – Достаточно ли у вас знаний о понятии «математическое моделирование»? Формулирует учебную задачу: – Исследовать понятие «математическое моделирование» | Записывают слова, которые у них ассоциируются с понятием «математическое моделирование». Например: математические модели, математическое описание, математический аппарат. Анализируют полученные слова. Приходят к выводу о своем понимании «математического моделирования» Осознают важность решения поставленной учебной задачи | Развитие навыков целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – усвоить суть понятия «математическое моделирование»; – научиться осуществлять математическое моделирование | Умение принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов. – Почему мне нужно знать, что такое «математическое моделирование»? – Почему мне нравится изучать новые темы по алгебре? – Насколько важно для меня научиться на уроке алгебры новым умениям? – Какова моя цель на данном уроке? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Умение выражать свои мысли, демонстрировать самомотивацию |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – Как можно использовать язык математики для решения научных задач? Организует анализ определения понятия «математическое моделирование».
Рассматривает с учащимися образцы прикладных задач и соответствующие им математические модели. | Прикладная задача | Математическая модель | | Один килограмм картофеля стоит 24 р. Сколько картофеля можно купить за 120 р.? | Чему равно частное 120 : 24? | | В магазине есть 3 вида чашек и 2 вида тарелок. Сколько существует способов составить набор из одной чашки и одной тарелки? | Чему равно произведение 3 . 2? | | На стоянке было несколько автомобилей. Когда 5 машин уехало, осталось 2 машины. Сколько автомобилей было на стоянке сначала? | Найдите корень уравнения х – 5 = 2 | Предлагает обучающимся провести исследование и выяснить, из каких этапов состоит решение прикладной задачи. Стимулирует самостоятельную познавательную деятельность обучающихся.
Организует анализ решения задачи: – Масса деревянной балки составляет 120 кг, а масса железной балки – 140 кг, причем железная балка на 1 м короче деревянной. Какова длина каждой балки, если масса 1 м железной балки на 5 кг больше массы 1 м деревянной? Совместно с учащимися выделяет этапы решения прикладной задачи.
Предлагает обучающимся самостоятельно решить задачу: – Из двух пунктов, расстояние между которыми равно 18 км, вышли одновременно навстречу друг другу два туриста и встретились через 2 ч. С какой скоростью шел каждый турист, если для прохождения всего расстояния между пунктами первому из них нужно на 54 мин больше, чем второму? Организует процесс сравнения решения задачи обучающихся с решением из учебника. Помогает обучающимся понять логику решения задачи из учебника.
Предлагает совместно решить задачу: – Два работника могут вместе выполнить производственное задание за 10 дней. После 6 дней совместной работы первого из них перевели на другое задание, а второй продолжал работать. Через 2 дня самостоятельной работы второго оказалось, что сделано 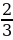 всего задания. За сколько дней каждый работник может выполнить это производственное задание, работая самостоятельно? всего задания. За сколько дней каждый работник может выполнить это производственное задание, работая самостоятельно? | Принимают участие в обсуждении проблемного вопроса. Предлагают идеи. Строят гипотезы.
Проводят исследование. Анализируют определение. Задают вопросы учителю. | Определение | Вопрос учителю | | Математическое моделирование – область математики, которая занимается построением и изучением математических моделей | Каким образом…?
| Принимают участие в обсуждении образцов прикладных задач и математических моделей. Задают вопросы учителю. Пытаются самостоятельно придумать прикладную задачу и соответствующую ей математическую модель.
Осуществляют поиск информации. Анализируют найденную информацию. Составляют вопросы для дополнительных исследований. | Найденная информация | Надо дополнительно узнать… Меня интересует… | | Этапы решения прикладной задачи: 1) Построение математической модели. 2) Решение математической задачи. 3) Анализ полученного результата, исходя из содержания прикладной задачи | Как…?
Почему…? | Анализируют решение задачи. Формулируют вопросы учителю. | Решение задачи | Мне непонятно… Вопросы учителю | | I этап. Пусть длина деревянной балки равна х м, тогда длины железной составляет (х – 1) м. Масса 1 м деревянной балки равна 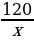 кг, а масса 1 м железной кг, а масса 1 м железной 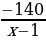 кг. Тогда разность кг. Тогда разность 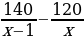 показывает, на сколько масса 1 м железной балки больше массы 1 м деревянной балки. По условию задачи эта разность равна 5 кг. Тогда получаем уравнение показывает, на сколько масса 1 м железной балки больше массы 1 м деревянной балки. По условию задачи эта разность равна 5 кг. Тогда получаем уравнение 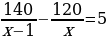 . Это уравнение и является математической моделью данной прикладной задачи . Это уравнение и является математической моделью данной прикладной задачи | Каким образом…? | | II этап. Решение уравнения. 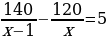
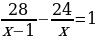
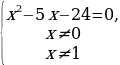
х = 8 или х = –3 | Почему…? | | III этап. Анализ результата, полученного на II этапе, исходя из содержания прикладной задачи. Корень –3 не удовлетворяет условию задачи, поскольку такая величины, как длина, не может выражаться отрицательным числом. Следовательно, длина деревянной балки равна 8 м, а длина железной – 7 м. Ответ: 8 м, 7 м. | Как…? | Решают задачу. Анализируют решение задачи. Сравнивают со своими идеями решения задачи. Проводят дополнительные исследования. | Решение задачи из учебника | Сравнение с собственным решением | | Пусть скорость первого туриста равна х км/ч, а второго – у км/ч, х у. До встречи первый турист прошел 2х км, а второй турист прошел 2у км. Вместе они прошли 18 км. Тогда 2х + 2у = 18. Расстояние между пунктами первый турист проходит за 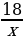 ч, а второй – за ч, а второй – за 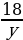 ч. Так как первому туристу для прохождения этого расстояния нужно на 54 мин = ч. Так как первому туристу для прохождения этого расстояния нужно на 54 мин = = 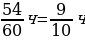 больше, чем второму, то больше, чем второму, то 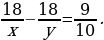
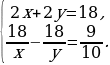
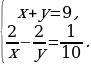
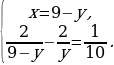
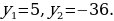
Корень 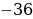 не подходит по смыслу задачи. Следовательно, у = 5, х = 4, то есть скорость первого туриста 4 км/ч, а скорость второго 5 км/ч. не подходит по смыслу задачи. Следовательно, у = 5, х = 4, то есть скорость первого туриста 4 км/ч, а скорость второго 5 км/ч. Ответ: 4 км/ч, 5 км/ч.
|
| Решают задачу вместе с учителем. | Решение задачи | Комментарии обучающихся | | Пусть первый работник может выполнить все задание за х дней, а второй – за у дней. За 1 день первый рабочий выполняет 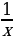 часть задания, а за 10 дней – часть задания, а за 10 дней – 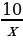 часть задания. Второй работник за 1 день выполняет часть задания. Второй работник за 1 день выполняет 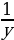 часть задания, а за 10 дней – часть задания, а за 10 дней – 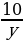 часть задания. Так как за 10 дней совместной работы они выполняют все задание, то часть задания. Так как за 10 дней совместной работы они выполняют все задание, то 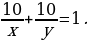
Первый работник работал 6 дней и выполнил 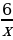 часть задания, а второй работал 8 дней и выполнил часть задания, а второй работал 8 дней и выполнил 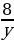 часть задания. Так как в результате было выполнено часть задания. Так как в результате было выполнено 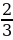 задания, то задания, то 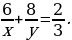 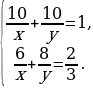
х = 15, у = 30. Следовательно, первый работник может выполнить задание за 15 дней, а второй – за 30 дней. Ответ: 15 дней, 30 дней. |
|
| Умение выражать свои мысли в соответствии с задачей Умение анализировать информацию
|
| VI. Закрепление изученного материала | Организует конкурс на составление лучшего вопроса по изученному новому материалу на уроке. | Придумывают вопросы. Отвечают на вопросы одноклассников. Вместе с учителем определяют лучший вопрос. Примеры вопросов: – Можно ли любую задачу по математике называть прикладной? – Из каких этапов состоит решение прикладной задачи? – Для чего нужно математическое моделирование? | Умение осуществлять актуализацию полученных знаний и умений |
| VII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами. – Что показал данный урок? – Доволен ли я результатами своей работы? – Что мне больше всего запомнилось на уроке? – Могу ли я сформулировать новые цели в своем стремлении изучать алгебру? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Умение отслеживать цель учебной деятельности |







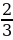 всего задания. За сколько дней каждый работник может выполнить это производственное задание, работая самостоятельно?
всего задания. За сколько дней каждый работник может выполнить это производственное задание, работая самостоятельно?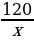 кг, а масса 1 м железной
кг, а масса 1 м железной 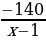 кг. Тогда разность
кг. Тогда разность 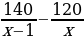 показывает, на сколько масса 1 м железной балки больше массы 1 м деревянной балки. По условию задачи эта разность равна 5 кг. Тогда получаем уравнение
показывает, на сколько масса 1 м железной балки больше массы 1 м деревянной балки. По условию задачи эта разность равна 5 кг. Тогда получаем уравнение 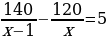 . Это уравнение и является математической моделью данной прикладной задачи
. Это уравнение и является математической моделью данной прикладной задачи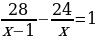
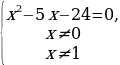
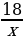 ч, а второй – за
ч, а второй – за 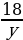 ч. Так как первому туристу для прохождения этого расстояния нужно на 54 мин =
ч. Так как первому туристу для прохождения этого расстояния нужно на 54 мин = 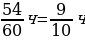 больше, чем второму, то
больше, чем второму, то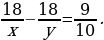
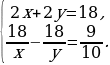
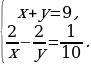
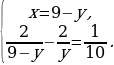
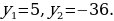
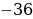 не подходит по смыслу задачи. Следовательно, у = 5, х = 4, то есть скорость первого туриста 4 км/ч, а скорость второго 5 км/ч.
не подходит по смыслу задачи. Следовательно, у = 5, х = 4, то есть скорость первого туриста 4 км/ч, а скорость второго 5 км/ч.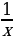 часть задания, а за 10 дней –
часть задания, а за 10 дней – 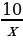 часть задания. Второй работник за 1 день выполняет
часть задания. Второй работник за 1 день выполняет 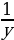 часть задания, а за 10 дней –
часть задания, а за 10 дней – 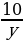 часть задания. Так как за 10 дней совместной работы они выполняют все задание, то
часть задания. Так как за 10 дней совместной работы они выполняют все задание, то 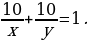
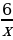 часть задания, а второй работал 8 дней и выполнил
часть задания, а второй работал 8 дней и выполнил 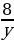 часть задания. Так как в результате было выполнено
часть задания. Так как в результате было выполнено