| (Ф/И) В тетрадях учащихся и на доске рисунок трапеции и записи:
1. В Основание С 
Боковая сторона Боковая сторона
А Основание D
АВСD - трапеция, если ВС ǁ АD, АВ и СD - боковые стороны, ВС и АD – основания
2. В С 
  М М 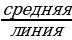 N N
А D
АВСD - трапеция, АM=ВМ, СN=DN, то МN - средняя линия трапеции.
3. Свойство средней линии трапеции.
Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. В С  
  М N М N
 А D K А D K
Доказательство: АВСD - трапеция, МN - средняя линия трапеции. Проведем ВК через вершину В и середину N боковой стороны СD. Она пересекает АD в некоторой точке К. Рассмотрим два треугольника NBC и NKD. CN=DN (по построению) ∟ BNC=∟ KND (как вертикальные) ∟ NCB=∟ NDK (как внутренние накрестлежащие при ВС ǁ АК и секущий СD)   Значит NBC= NKD (по второму признаку равенства треугольников). Тогда BN=KN и ВС=DK Значит МN - средняя линия треугольника АВK. По свойству средней линии треугольника МN ǁ АК и МN=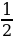 АК= АК=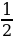 (АD+ DK)= (АD+ DK)= 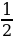 (АD+ ВС) (АD+ ВС) Значит МN ǁ АD и ВС и МN= 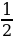 (АD+ ВС). (АD+ ВС). Ввести понятие равнобедренной и прямоугольной трапеции.      В С В С В С В С
  
  
А D А D
АВ = СD ∟А = ∟В =90 0
| 






 М
М 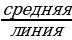 N
N
 А D K
А D K
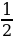 АК=
АК=


 В С В С
В С В С











 В 6см С
В 6см С М N
М N P R
P R
 В С
В С М K N
М K N
 М 25см K
М 25см K 









