Технологическая карта урока Рациональные числа

Тема

Целые числа. Рациональные числа.

Цели

Образовательные: закрепить знания по теме: Координатная прямая. Ввести понятия целых и рациональных числел.

Формировать УУД:  формировать умение находить противоположные числа.

Личностные УУД (ЛУУД): Объясняют самому себе свои отдельные ближайшие цели саморазвития, проявляют положительное отношение к урокам математики, дают самооценку результатов своей учебной деятельности.

Регулятивные УУД (РУУД): определяют цель учебной деятельности, осуществляют поиск средств её достижения.

Познавательные УУД (ПУУД): Закрепить знания по пройденным темам

Планируемые результаты

Предметные:  закрепить знания по теме координатная прямая, положительные и отрицательные числа

Уметь: определять противоположные числа, целые и рациональные числа

Метапредметные: формировать умение определять понятия, создавать обобщения, устанавливать аналогии.

Ученик получит возможность научится переводить текст задачи на математический язык, осуществлять контроль своей деятельности в процессе достижения результата

Основные понятия

Целые числа. Рациональные числа.

Ресурсы:

• основные

• дополнительные

презентация, проектор, индивидуальные карточки, Экран, учебник «Математика 6 класс» Мерзляк А.Г., рефлексия.

Организация пространства

Индивидуальная, фронтальная, парная

Этапы урока

Деятельность

Учителя-

Деятельность

учеников

I. Организационный

(2 мин)

- (1 слайд, улыбающееся солнце с лучиками) Здравствуйте, ребята! Присаживайтесь. Чтобы наш урок прошёл сегодня в тёплой дружеской атмосфере, давайте подарим друг другу частичку тепла: потрите свои ладошки так, чтобы они стали тёплыми. А теперь прикоснитесь к ладошкам соседа – подарите своё тепло и возьмите от него частичку теплоты.

- Огромное солнце не делим на части,

И вечную землю нельзя поделить.

А капельку счастья, тепла и удачи

Ты можешь всегда подарить.

-И я дарю вам всем своё тепло и желаю удачи.

- Ребята, обратите внимание, на партах у каждого из вас лежат рабочие листы. (приложение №1)

В них есть задания, которые вы будете выполнять в течение нашего урока, а также оценивать свою работу и соседа по парте. И в конце урока подведем итоги. Подпишите их, пожалуйста.

Приготовиться к уроку, настроиться на работу

Дети подписывают рабочие листы.

II. Актуализация опорных знаний

1. Математический диктант.

Итак, 1 задание - математический диктант. Я буду зачитывать высказывания, а вы на обратной стороне оценочного листа запишите «+» если данное утверждение верно, «-» если утверждение не верно. (слайд 2)

1. Натуральные числа - это числа, которые используют при счёте. (+)

2. Наименьшим натуральным числом является 0. (-)

3. Наибольшее натуральное число - это 1000. (-)

4. Обыкновенная дробь - это частное двух чисел, записанное определенным образом.(+)

5. Натуральное число всегда можно представить в виде обыкновенной дроби со знаменателем 1. (+)

6. 0, 5 это половина единицы. (+)

7. 0, 25 это треть единицы. (-)

8. Любое число можно представить в виде десятичной дроби. (-)

9. Точка с координатой минус десять на координатной прямой находится правее начала координат.(-)

10. Точка с координатой минус два на координатной прямой находится левее начала отсчета (+)

Проведите взаимопроверку с помощью ключа: + - - + + + - - - +, таблица оценивания (слайд 3):

5-6б «3»;

7-8б «4»;

9-10б «5»;

Подсчитайте верно выполненные задания, запишите количество баллов в оценочный лист. Какие утверждения у вас вызвали сомнения? Поднимите руки, кто справился с разминкой на 10 баллов. Молодцы!

1. Постановка основной цели и формулирование темы урока.

«Сущность вещей есть число, которое вносит во всё единство и гармонию» (слайд 4)

Это высказывание о числах принадлежит древнегреческому математику, философу – идеалисту Пифагору. Мы с вами живем в мире чисел, а в школьные годы учимся работать с ними. Вот и сегодня мы продолжаем эту работу.

- Скажите, какие числа вы знаете?

- Какие числа называются натуральными?

- Приведите примеры положительных чисел.

- Назовите отрицательные числа.

- Какие числа называются дробными?

- Что вы можете сказать о целых числах?

- Какие числа относятся к целым?

- Правильно, но есть и другие числа, которые тоже считаются целыми.

- А какие числа называются рациональными?

Этот вопрос вызвал у вас наибольшее затруднение, так как вы не знакомы с данным математическим понятием.

- Значит, с какими числами мы будем работать на сегодняшнем уроке?

Правильно, а также вы узнаете всё о целых числах.

- Какова же основная цель нашего урока? (слайд 5)

- Давайте попробуем сформулировать тему сегодняшнего урока:

- (слайд 6) Откройте тетради, запишите число: 24.01, классная работа и тема урока: Целые числа. Рациональные числа.

Работа в рабочих листах.

Выполняют взаимопроверку с помощью ключа и записывают количество баллов в оценочный лист

Работают по презентации

Ответы детей: натуральные, положительные, отрицательные, дробные.

Числа, которые мы употребляем при счёте предметов: 1, 2, 3, …

Приводят примеры.

Приводят примеры.

Числа, которые представлены в виде дроби

У них нет дроби.

2, 7, 13, …

?

С рациональными.

Познакомиться с целыми и рациональными числами.

Целые числа. Рациональные числа.

Дети записывают в тетради.

Антонимы

Антонимы – это слова одной части речи, различные по звучанию и написанию, имеющие прямо противоположные лексические значения.

Наверное, да.

Числа.

Положительные и отрицательные.

Нет.

А и С.

6 единичных отрезков.

Записывают в тетради.

0.

Записывают правило.

III Изучение нового материала.

- А сейчас послушайте меня внимательно, в русском языке вы изучали такие пары слов: громко – тихо, молодой – старый, много – мало, да – нет. Как они называются?

- Что это такое «антонимы»?

- А как вы думаете, в математике есть что-нибудь противоположное?

- И что же это?

- Какие числа, на ваш взгляд, можно назвать противоположными?

- Давайте подумаем, а все ли положительные числа противоположны отрицательным? Например, число «5» будет противоположно числу «-2»?

• (Слайд 7) Рассмотрим координатную прямую, на которой отмечены точки: А (-6), В(-1,5), С(6), D(1,2), E(-3 )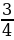

1. Какие точки одинаково удалены от начала отсчета и находятся по разные стороны от нее?

2. Чему равно расстояние (в един. отрезках) от точки О (начала отсчета) до точек А и С?

- Числа 6 и -6 называются противоположными.

Обозначение: (Слайд 8)

-а означает число, противоположное числу а

-(-а)=а. (число, противоположное числу – а равно а) Запишите это в тетрадь.

- Как вы думаете, какое число противоположно 0?

Правильно:

(Слайд 9)

Целые числа

Противоположные натуральным

Натуральные числа

Нуль

- Запишите правило из учебника в тетрадь на стр.187.

И если к целым числам добавить дробные, то вместе они образуют рациональные числа

Слайд 7 Рациональные числа (схема) Слайд 10

Рациональные числа

Целые числа

Дробные числа

Противоположные натуральным

Натуральные числа

Нуль

Вывод: То есть, все числа, которые вам известны, относятся к множеству рациональных чисел.

4.Физкультминутка

Ребята, а теперь немного подвигаемся. Встаньте ровно между рядами. Вспомним уличный термометр. Я называю числа

Если температура отрицательная (число отрицательное), то присели на корточки, если положительная, то поднимаете руки вверх.

- 3; 5; -1; 8; - 7; 0; – 2; 15; 4;

Выполняют физкультминутку

IV.Первичное закрепление материала.

Ну вот немного отдохнули и продолжаем нашу работу

- Выполним устно № 871. Найдите его в учебнике.

- Молодцы! А теперь №874.

И поработаем с №875

Работают с учебником, отвечают устно

№871:

1)-6; 2)7; 3)-0,9; 4)0; 5)-7,2; 6)23; 7)13,4

№ 874:

1)да; 2)да; 3)да; 4)нет; 5)да; 6) да; 7)нет; 8)да; 9) да; 10)нет

№875:

1. 5; 324;35; 976

2. 5;-7;0; -125; 324; -2; 35; -79; 976

3. 5; ½; 8,6; 324; 15 3/7; 35; 13,65; 976

4. -7; 0; -3,7; -125; -27 11/19; -2; -79

5. -7; -125; -2; -79

6. ½; 8,6; 15 3/7; 13,65

IV. Применение новых знаний.

1. Работа в учебнике

1)№880 выполним письменно в тетради, один учащийся у доски

2. Самостоятельная работа

2)Слайд 11 Ребята, а сейчас вам надо выполнить небольшую самостоятельную работу. На листах у вас даны вопросы и ответы к ним. Вы должны стрелками соединить вопрос и правильный ответ к нему. (приложение 2) Слайд 12

Оцените свою работу и поставьте оценку в рабочий лист

3б «3»;

4б «4»;

5б «5»;

3. Работа в парах

3) Теперь по новой теме предлагаю вам самостоятельно составить кластер.

Дам подсказку, вам нужно только правильно расположить карточки, то есть найти их правильное место.

У вас на партах разрезанные листы с названием чисел, которые вы уже знаете и с которыми сегодня познакомились.

Составьте из них схему (приложение 3)

Слайд 13

Натуральные числа

1)работают у доски и на местах

№ 880:

5; 4; 3; 2; 1;

-5; -4; -3; -2; -1 Единичный отрезок в 1 клетку

2) работают самостоятельно на листах и сверяют с доской. Выставляют оценки в рабочий лист

Составляют схему, сверяют с доской правильность составления

Рациональные числа

Дробные числа

Целые числа

Противоположные натуральным

Десятичные дроби

Обыкновенные дроби

Нуль

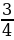VI. Рефлексия учебной деятельности на уроке

1. С какими понятиями мы познакомились сегодня на уроке?

2. Какие числа называют целыми и рациональными?

3. Какие числа называют рациональными?

Мы достигли основной цели урока? Слайд 14

Целые и рациональные числа

Целые числа – это натуральные, противоположные натуральным и нуль

Рациональные числа – это целые и дробные числа

Да, достигли

7. Задание на дом. Выставление оценок

Д/з п.31 №879,881 Слайд 15

Выставление оценок

Записывают д/з