Тела вращения. Решение задач.

ТЕЛА ВРАЩЕНИЯ

РЕШЕНИЕ ЗАДАЧ

Основные формулы

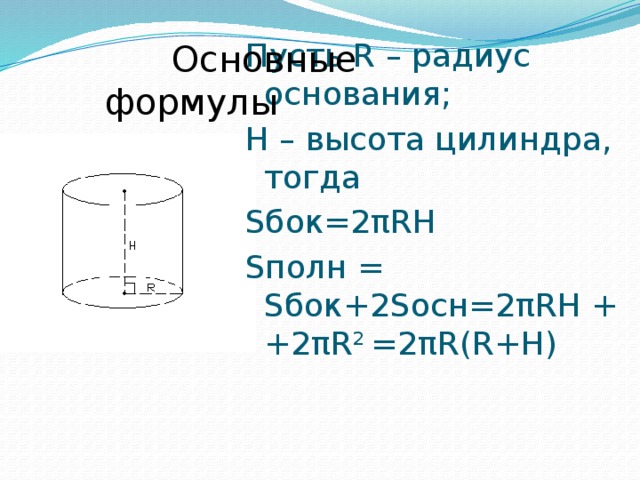
Пусть R – радиус основания;

H – высота цилиндра, тогда

Sбок=2πRH

Sполн = Sбок+2Sосн=2πRH + +2πR 2 =2πR(R+H)

Основные формулы

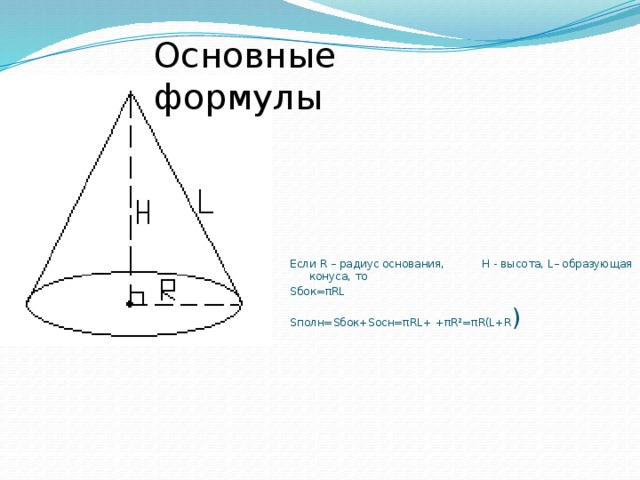
Если R – радиус основания, H - высота, L– образующая конуса, то

Sбок=πRL

Sполн=Sбок+Sосн=πRL+ +πR²=πR(L+R )

Усеченный прямой конус

h – высота усеченного конуса ; R и R1 – радиусы его верхнего и нижнего оснований; l – его образующая

Формулы:

Основные формулы

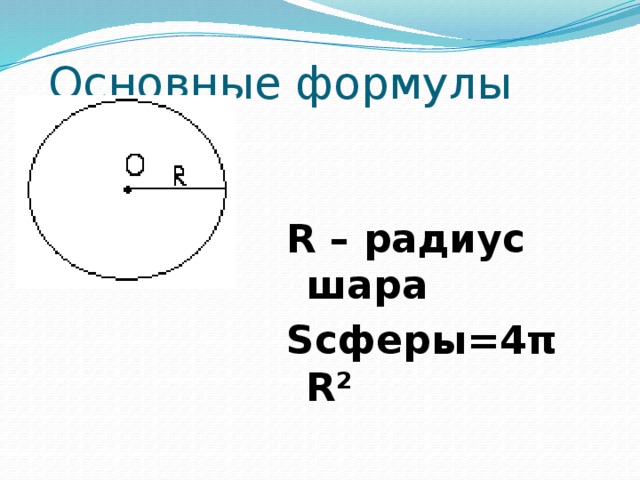
R – радиус шара

Sсферы=4πR²

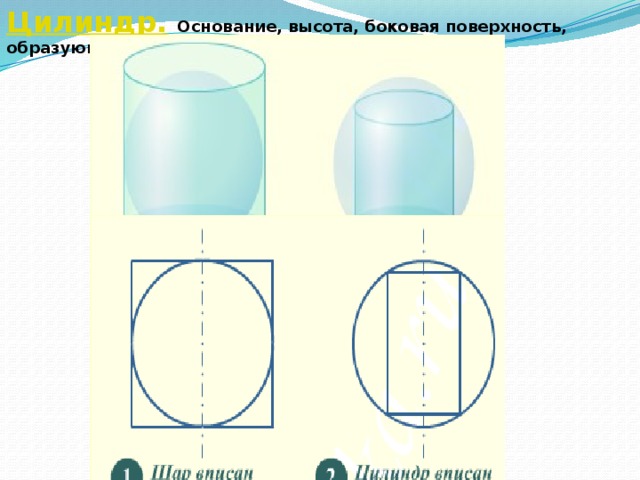
Цилиндр.   Основание, высота, боковая поверхность, образующая, развертка

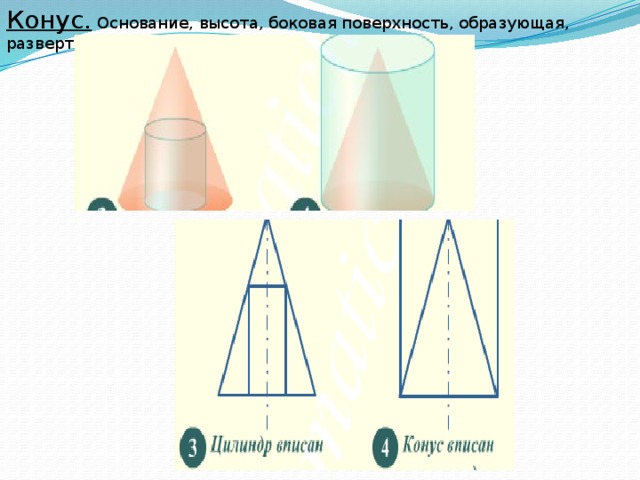
Конус.   Основание, высота, боковая поверхность, образующая, развертка

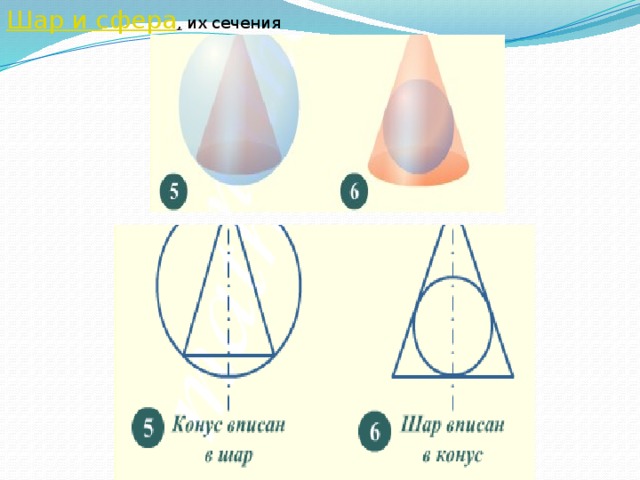
Шар и сфера ,   их сечения

Задача 1.

Шар вписан в цилиндр. Площадь поверхности шара равна 111.

Найдите площадь полной поверхности цилиндра.

Решение.

Площадь полной поверхности цилиндра находим по формуле  S ц  = 2 πrh  + 2 πr 2 .

Из рисунка (1) для плоского

сечения видно, что радиус

основания цилиндра ( r ) равен

радиусу вписанного шара ( R ),

а его высота ( h ) равна диаметру

шара (удвоенному радиусу).

Поэтому  S ц  = 2 πR ·2 R  + 2 πR 2  = 6 πR 2 . Величину  πR 2  найдем из формулы поверхности шара  S ш  = 4 πR 2 . Следовательно,  πR 2  =  S ш  / 4 = 111/4. Окончательно находим  S ц  = 6·111 / 4 = 333/2 = 166,5.

Ответ:  166,5

Задача 2

В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найти высоту цилиндра, если радиус его основания равен 4.

Дополним чертеж осевого сечения радиусом шара и расставим буквы для обозначения отрезков.  Площадь поверхности шара  S ш  = 4 πR 2  = 100π. Отсюда  R 2  = 25 и  R  = 5. В треугольнике  OAB :  OA  =  x  - половина искомой высоты цилиндра;  AB  = 4 - радиус основания цилиндра;  OB  = 5 - радиус шара.  По теореме Пифагора: x 2  + 4 2  = 5 2  ,

x 2  = 25 − 16 = 9;  x  = 3.  h  = 6.

Ответ:  6

Задача 3

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса.

  l  2  =  h  2  +  r  2 По условию задачи  h  =  r , следовательно  l  2  =  r  2  +  r  2 ;    l  2  = 2 r  2 ;     l  = √2· r . Площадь боковой поверхности цилиндра  S ц  = 2 πrh  = 2 πr  2 . Площадь боковой поверхности конуса  S к  =  πrl  =  πr ·√2· r  = √2 πr  2 ; т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно  S к  = 3√2 / √2 = 3/ Ответ:  3 A C B " width="640"

Воспользуемся чертежом осевого сечения, расставим буквы для обозначения отрезков:  AC  =  h  - высота конуса и цилиндра,  CB  =  r  - радиус оснований конуса и цилиндра,  AB  =  l  - образующая цилиндра.

Из треугольника  ABC  по теореме Пифагора: AB 2  =  AC 2  +  CB 2  ==  l  2  =  h  2  +  r  2 По условию задачи  h  =  r , следовательно  l  2  =  r  2  +  r  2 ;    l  2  = 2 r  2 ;     l  = √2· r . Площадь боковой поверхности цилиндра 

S ц  = 2 πrh  = 2 πr  2 . Площадь боковой поверхности конуса  S к  =  πrl  =  πr ·√2· r  = √2 πr  2 ;

т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно  S к  = 3√2 / √2 = 3/ Ответ:  3

A

C

B

Задача 4

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 7√2. Найдите радиус сферы.

Так как по условию задачи центр сферы находится в центре основания конуса, то основание конуса, в свою очередь, является диаметральным сечением сферы. Т.о. на плоском чертеже отрезок  AB  является диаметром окружности, и ∠ ACB  = 90° как вписанный угол, опирающийся на её диаметр.

Пусть  l  = 7√2 - образующая конуса,  R  - радиус сферы. Тогда в прямоугольном треугольнике  ABC   AC  =  BC  =  l  - катеты,  AB  = 2 R  - гипотенуза. По теореме Пифагора AB 2  =  AC 2  +  BC 2 ; (2 R ) 2  =  l  2  +  l  2 ; 4 R  2  =  l  2  +  l  2  = 2 l  2 ;   4 R  2  = 2(7√2_) 2 ; 4 R  2  = 2·49·2 = 4·49;    R  2  = 49;   R  = 7.

Ответ:  7

Задача 5

Найти площадь поверхности шара, описанного около конуса, у которого радиус основания   2/√π, а высота   1/√π.

Пусть  R  - радиус сферы. Поскольку  СD  - диаметр окружности осевого сечения, то  СH  +  HD  = 2 R . Воспользуемся свойством пересекающихся хорд окружности, чтобы найти длину отрезка  HD  =  x .

DH·HС = AH·HC; x ·  1/√π =   2/√π ·  2/√π; Преобразуя, получим  х  =   4/√π.  2 R  =   1/√π +   4/√π =  5/√π;    R  =  5/2√π. Площадь сферы  S  = 4π R 2  = 4π·25/4π = 25.

Ответ:  25

Задача 5

В шар вписан конус, образующая которого равна диаметру основания. Найти отношение полной поверхности этого конуса к поверхности шара.

Пусть образующая конуса ( AC  =  BC ) равна  a . Тогда по условию задачи диаметр конуса ( AB ) тоже равен  a . То есть, треугольник  ABC  - равносторонний.

Чтобы найти радиус шара ( R ), используем формулу, связывающую длину стороны равностороннего треугольника и радиус описанной около него окружности.

Радиус основания конуса  r  =  a /2 (половина диаметра).

Площадь полной поверхности конуса S к  = π r ( r  +  l ) = π· a /2·( a /2 +  a ) = 3π a 2 /4.

Площадь поверхности шара S ш  = 4π R 2  = 4π· a 2 ·(√3/3) 2  = 4π a 2 /3.

Их отношение

S к / S ш  = 3π a 2 /4/4π a 2 /3 =  9/16 = 0,5625.

Ответ:  0,5625

ЗАДАНИЕ НА ДОМ

№ 616

Задачи ЕГЭ (распечатка)