Тема : "Окружность" 8 класс. Презентация.

геометрия

(автор учебника Л.С. Атанасян)

8 класс

Работу выполнила учитель

математики Гоптарь Л.И.

Глава VIII

Окружность

§1 Касательная к окружности

§2 Центральные и вписанные углы

§3 Четыре замечательные точки

треугольника

§4 Вписанная и описанная окружности

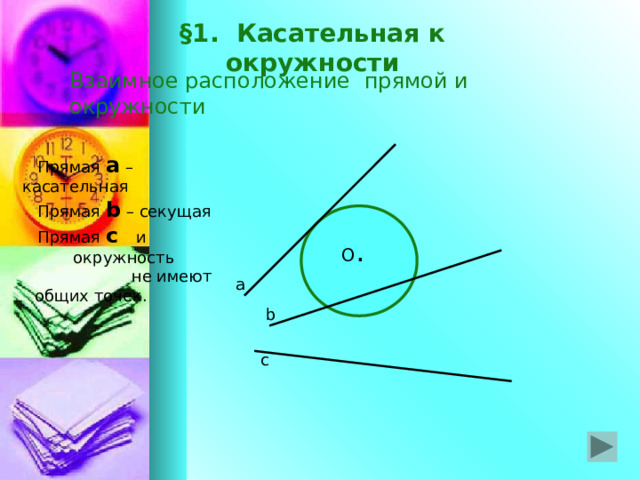
§1. Касательная к окружности

Взаимное расположение прямой и окружности

Прямая а – касательная

Прямая b – секущая

Прямая с и

окружность не имеют общих точек.

О .

a

b

c

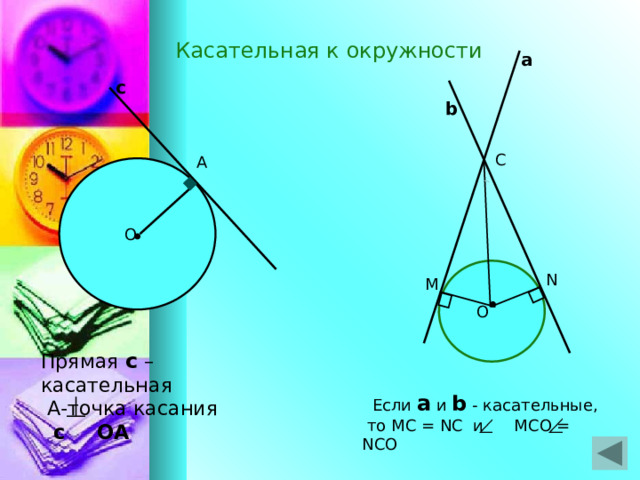
Касательная к окружности

a

c

b

С

А

О

О

N

М

Прямая с – касательная

А-точка касания

c ОА

Если а и b - касательные,

то MC = NC и MCO = NCO

§2. Центральные и вписанные углы

Центральный угол

Градусная мера

дуги окружности

А

В

В

ᵕ АВ= АОВ

о

O

А

ᵕ АМВ=360º – АОВ

М

Вписанный угол

А

L

В

ᵕ АLВ= 180º

.

.

О

B

O

С

А

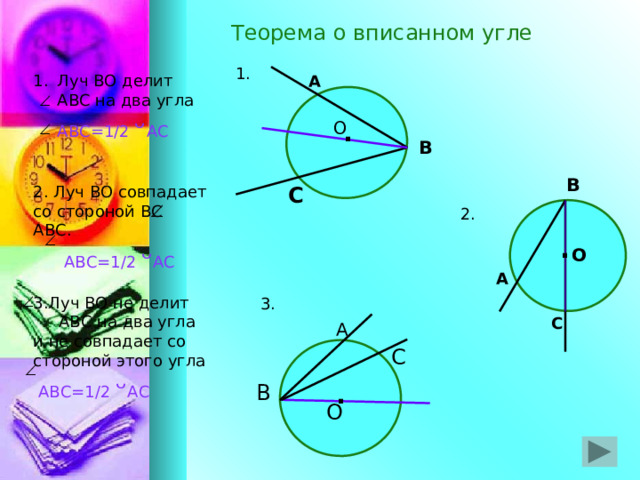
Теорема о вписанном угле

1.

• Луч ВО делит АВС на два угла АВС=1/2 ᵕ АС

2. Луч ВО совпадает со стороной ВС АВС.

АВС=1/2 ᵕ АС

3.Луч ВО не делит АВС на два угла и не совпадает со стороной этого угла

АВС=1/2 ᵕ АС

А

.

О

B

В

С

2.

.

О

А

3.

С

А

С

.

B

О

Свойства вписанных углов

D

A

C

S

B

1.

2.

E

C

.

О

F

A

N

B

М

С= D= E= 90°

F= C= S= А= В

D

A

Свойство пересекающихся хорд

Е

AB ∩ CD=Е,

АЕ • ВЕ=СЕ • DЕ

B

C

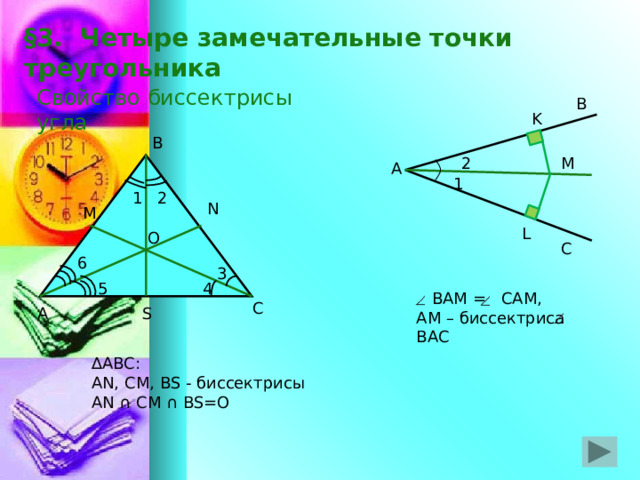
§3. Четыре замечательные точки треугольника

Свойство биссектрисы угла

B

K

В

M

2

А

1

1

2

N

M

L

O

C

6

3

5

4

ВАМ = САМ,

АМ – биссектриса ВАС

С

S

А

∆ АВС:

AN, CM, BS - биссектрисы

AN ∩ CM ∩ BS=О

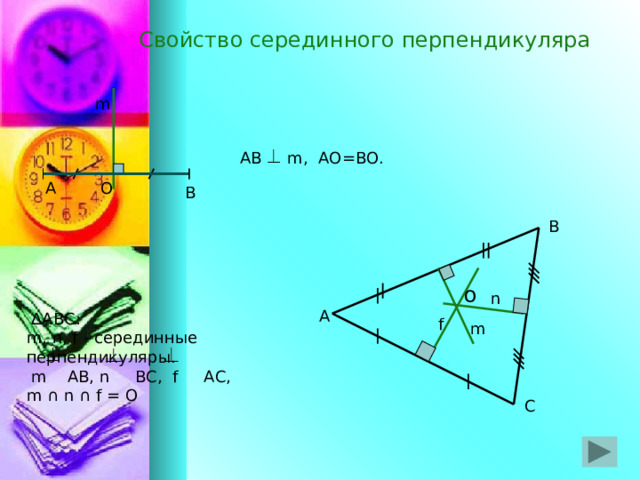
Свойство серединного перпендикуляра

m

AB m, АО=ВО.

A

О

B

В

o

n

А

∆ АВС:

m, n, f - серединные перпендикуляры.

m АВ, n ВС, f АС,

m ∩ n ∩ f = О

f

m

С

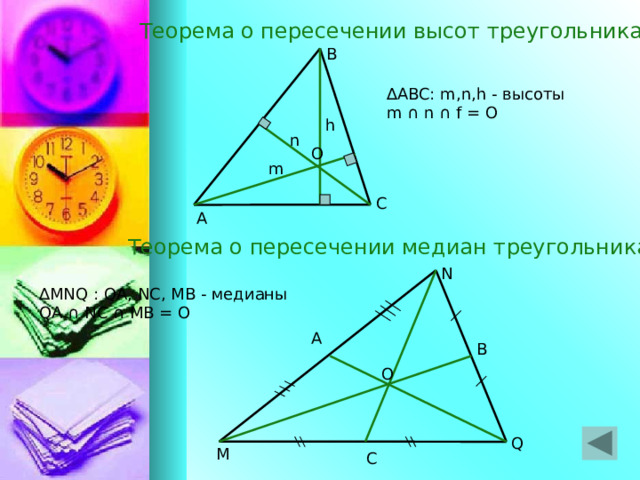
Теорема о пересечении высот треугольника

В

∆ ABC: m,n,h - высоты

m ∩ n ∩ f = О

h

n

О

m

С

А

Теорема о пересечении медиан треугольника

N

∆ MNQ : QA, NC, MB - медианы

QA ∩ NC ∩ MB = О

А

В

О

Q

M

С

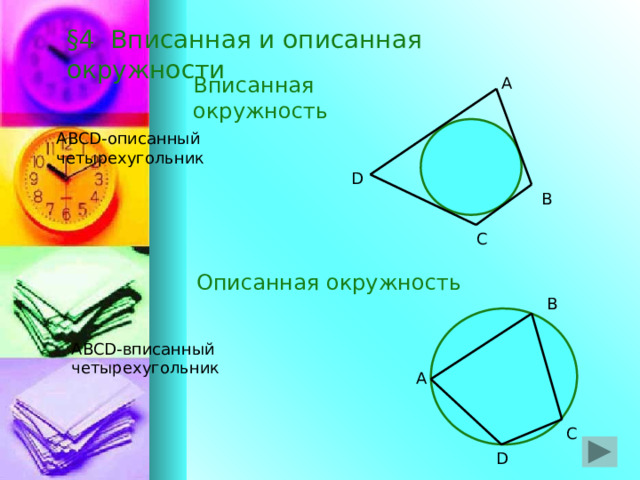
§4 Вписанная и описанная окружности

Вписанная окружность

А

ABCD-описанный четырехугольник

D

В

С

Описанная окружность

B

ABCD-вписанный четырехугольник

A

C

D

Вписанный многоугольник

∆ АВС – вписанный в окружность

А

Около любого треугольника можно описать окружность.

В

С

Описанный многоугольник

В любой треугольник можно вписать окружность.

Замечательные свойства четырехугольников

ABCD-описанный около окружности четырехугольник

AB+CD=BC+AD

А

D

В

N

С

M

E

F

MNEF-вписанный в окружность четырехугольник:

М + Е= F+ N.

Спасибо за внимание