Тема: Основные приемы работы в электронных таблицах
Цель: научиться графически решать уравнения в электронных таблицах.
Задание 1:
«Решить графически уравнение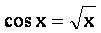 ».
».
Ход выполнения
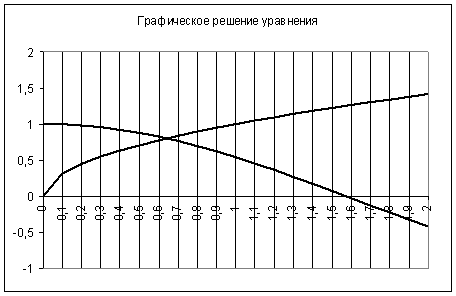
Для графического решения построим графики каждой из функций на отрезке [0, 2] с шагом (изменением х) 0.1. Чтобы построить графики функций для каждой функции построим таблицу значений, используя стандартные функции COS и КОРЕНЬ.
| x | cos(x) | корень(х) |
| 0 | 1 | 0 |
| 0,1 | 0,995 | 0,316228 |
| 0,2 | 0,9801 | 0,447214 |
| 0,3 | 0,9553 | 0,547723 |
| 0,4 | 0,9211 | 0,632456 |
| 0,5 | 0,8776 | 0,707107 |
| 0,6 | 0,8253 | 0,774597 |
| 0,7 | 0,7648 | 0,83666 |
| 0,8 | 0,6967 | 0,894427 |
| 0,9 | 0,6216 | 0,948683 |
| 1 | 0,5403 | 1 |
| 1,1 | 0,4536 | 1,048809 |
| 1,2 | 0,3624 | 1,095445 |
| 1,3 | 0,2675 | 1,140175 |
| 1,4 | 0,17 | 1,183216 |
| 1,5 | 0,0707 | 1,224745 |
| 1,6 | -0,029 | 1,264911 |
| 1,7 | -0,129 | 1,30384 |
| 1,8 | -0,227 | 1,341641 |
| 1,9 | -0,323 | 1,378405 |
| 2 | -0,416 | 1,414214 |
Примечание к построению диаграммы:
а) Для построения диаграммы выделяем столбцы cos(x) и корень(х).
б) При построении диаграммы на 2-ом шаге (Источник данных) нужно задать масштаб оси Х:
перейти на вкладку «Ряд»,
установить курсор в окно «Подписи оси Х»
выделить в таблице все ячейки столбца «х» от 0 до 2
нажать «Далее».
в) после построения графиков необходимо отредактировать точку пересечения осей
В результате построения графиков функций видно, что корень уравнения
приблизительно равен 0.64.
2. Решение текстовых задач с использованием формул
Решим задачу «Дана сторона квадрата. Вычислить его площадь и периметр».
Решение задачи.
а) Составим математическую модель задачи – перечислим формулы, используемые для ее решения: S = a; P = 4×a.
б) Подготовим таблицу решения:
в ячейку А1 введем название задачи, отцентрируем по группе ячеек А1:Е1
в ячейку А3 введем текст ввода, отцентрируем по группе ячеек А3:С3
в ячейку А4 введем текст площади, отцентрируем по группе ячеек А4:С4
в ячейку А5 введем текст периметра, отцентрируем по группе ячеек А5:С5
в ячейку D4 введем формулу площади =D3*D3
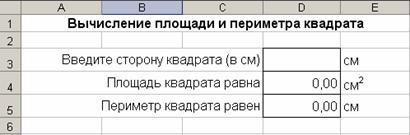
в ячейку D5 введем формулу периметра =4*D3
установим для группы ячеек D3:D5 числовой формат с двумя десятичными знаками;
отформатируем шрифт, выравнивание и обрамление ячеек.
в) Введем исходные данные и получим результаты.
В ячейку D3 введем значение стороны квадрата, в ячейках D4 и D5 получим соответственно значения площади и периметра. Результаты запишем в тетрадь.
3. Задачи, содержащие условие
Для решения задач, в которых в зависимости от выполнения какого-либо условия нужно выполнить разные действия используется функция проверки условия – функция ЕСЛИ.
Общий вид функции ЕСЛИ:
ЕСЛИ (; ; )
Условная функция, записанная в ячейку таблицы, выполняется так:
если условие истинно, то значение данной ячейки определяется значением , в противном случае – значением .
Условием функции ЕСЛИ является логическое выражение – выражение, записанное с помощью одного из знаков отношения: , =, =, . Такие выражения еще называют простыми условиями, например: A2=15; B2=$C$2.
Если в задаче требуется проверить несколько условий, то используется составное условие, полученное из нескольких простых с помощью логических операций: И, ИЛИ, НЕ, например: A2=15 И B2=$C$2; M15N15 ИЛИ $D$2 $K$12.
Результатом вычисления логического выражения являются логические величины ИСТИНА или ЛОЖЬ.
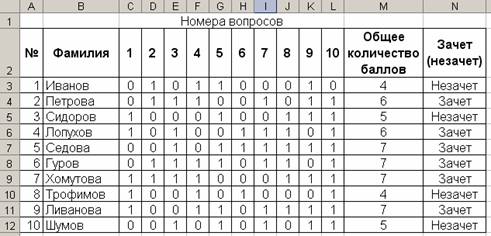
Задача №1
«Студенты сдают зачет, который предусматривает систему оценивания «Зачет» и «Незачет». Зачет ставится, если из 10 вопросов студент верно ответил больше, чем на половину вопросов, в противном случае ставится незачет. Надо автоматизировать процесс выставления зачета».
Решение:
заполнить таблицу по образцу;
в ячейках столбца M вычислить общее количество баллов с помощью автосуммирования;
в ячейку N3 ввести формулу =ЕСЛИ(M3=6;“Зачет”;“Незачет”)
скопировать эту формулу в ячейки N с помощью автозаполнения;
проанализировать полученный результат.
Задача №2.
«Даны коэффициенты a, b, c квадратного уравнения (a¹0). Определить, имеет ли это уравнение действительные корни или нет».
Решение:
В ячейку Е2 вводим формулу дискриминанта: =B3*B3-4*B2*B4
В ячейку G2 вводим формулу:
=ЕСЛИ(E2

Для получения результатов необходимо в ячейки B2, B3, B4 ввести исходные коэффициенты уравнения.
Задача №3
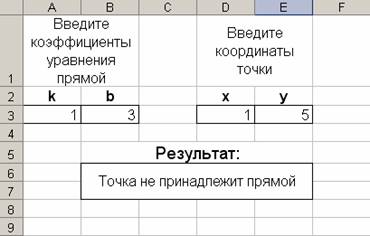
«Даны коэффициенты k и b уравнения прямой y=kx+b и даны координаты (x,y) точки на плоскости. Определить, принадлежит ли она данной прямой или нет».
Решение
В ячейку В6 вводим формулу:
=ЕСЛИ($A$3*$D$3+$B$3=$E$3;"Точка принадлежит прямой";"Точка не принадлежит прямой")
Для получения результатов необходимо в ячейки A3 и B3 ввести исходные коэффициенты прямой, а в ячейки D3 и E3 ввести исходные координаты точки.
Задача №4
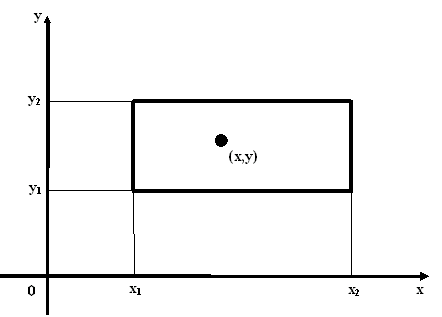
«Даны координаты вершин прямоугольника (х1,y1), (х1,y2), (х2,y1), (х2,y2), расположенного в первом квадранте, со сторонами, параллельными осям координат (0
Решение:
Если точка с координатами (x,y) лежит внутри прямоугольника или на его границе, то должны выполняться следующие условия:
x ³ x1 и x £ x2; y ³ y1 и y £ y2.
В ячейку G4 вводим формулу:
=ЕСЛИ(И($A$7=$A$3;$A$7=$B$3;$B$7
Получаем следующую таблицу:
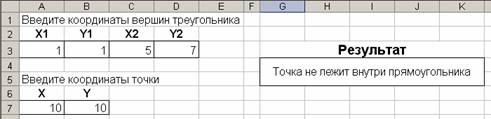
Для получения результатов необходимо в ячейки A3, B3, C3, D3 ввести исходные координаты вершин треугольника, а в ячейки A7, B7 ввести исходные координаты точки.
Результаты сохранить в папке на рабочем столе
























