План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Понятие о производной.
Тип урока - урок изучения нового материала.

Пусть дан график функции у=f(x).
Рассмотрим точку М0 с абсциссой xo. Пусть ∆х – это изменение абсциссы от точки xo до х, т.е. ∆х = х – xo , M0М – секущая, M0N – касательная.
Найдите:
а) угловой коэффициент секущей (это средняя скорость изменения функции);
б) угловой коэффициент касательной (подсказка: касательная – это предельное положение секущей)
Решение: у= f(x) – заданная функция, ∆х = х – xo – изменение абсциссы от точки xo до х.
vср =  . В нашем случае kсек =
. В нашем случае kсек =
При х→х0 (или ∆х →0) будет f(x)→f(x0), следовательно, M0М→ M0N.
Тогда k кас =  .
.

Рассмотрим движение материальной точки М по прямой с выбранным на ней началом отсчета – точкой О. Расстояние от начала отсчета до точки М в каждый момент времени t обозначим буквой s. Тогда движение точки М будет описываться функцией
s = s (t), t[ t0 ; t].
Найдите:
а) среднюю скорость за отрезок [t0 ; t];
б) скорость точки в момент времени t0 (мгновенную скорость).
Решение: За промежуток времени длительности t – t0 между моментами времени t0 и t точка проходит путь равный s(t) –s(t0 ).
Среднюю скорость получают, разделив перемещение материальной точки s на изменение времени, в течение которого оно совершено.
Тогда vср = ;
;
Чем меньше рассматриваемый промежуток времени, тем точнее можно охарактеризовать движение. А мгновенной скоростью называется число к которому стремится разностное отношение средней скорости за промежуток времени от t0 до t при t→ t0.
Тогда vмгн =  ,
,
Бактерии размножаются быстро и просто – они делятся пополам и при благоприятных условиях за сутки из одной бактерии могут образоваться десятки тысяч. Рост клеток бактерий в условиях ограниченности питательных веществ или пространства в течение начального интервала времени от t0 до t происходит по некоторому закону y = N(t).
Найдите:
а) среднюю скорость изменения количества бактерий за промежуток времени [t0 ; t];
б) скорость изменения количества точки в момент времени t0 (мгновенную скорость).
Решение: В физике для нахождения средней скорости делят длину перемещения тела s на время, в течение которого оно совершено,
т.е. vср = . В нашем случае vср =
. В нашем случае vср = .
.
Мгновенной скоростью v(t0) в момент времени t0 является число к которому стремится разностное отношение средней скорости за промежуток времени от t0 до t при t→ t0.
Тогда vмгн =  .
.
4. Изучение нового материала
Приращению аргумента соответствует «приращение функции», которое также обозначается с помощью заглавной греческой буквы «∆».
Вопрос: Скажите, а вы знаете, кто впервые стал использовать знак «∆» для обозначения разности аргументов?
- Да. Буква «∆» – одна из заглавных букв греческого алфавита ее стал использовать Эйлер (сер. 18 века).
Исходя из этого полученную формулу можно записать по-другому: или и прочитать так: число, к которому стремится разностное отношение  =
=  при
при  .
.
Поскольку многие задачи в различных областях науки в процессе решения приводят к такой же модели – этому отношению надо: дать название, дать обозначение и изучить его. Это мы с вами сейчас и сделаем.
(Слайд 4)
Определение: Производной функции  в точке
в точке  называется число, к которому стремится разностное отношение
называется число, к которому стремится разностное отношение  =
=  при
при  .
.
но обозначается по-разному:
 х),
х),  у′ – эти обозначения для производной ввел Жозеф Луи Лагранж
у′ – эти обозначения для производной ввел Жозеф Луи Лагранж
Это определение вы запишете в тетрадях.
Теперь посмотрите на ваши задачи и сформулируйте план нахождения производной.
(Учащиеся должны ответить):
(Слайд 5)
1. Задать функцию f(x).
Алгоритм нахождения производной (находим  )):
)):
1) Задать приращение  и вычислить
и вычислить  =
=  =
=  .
.
2) Найти разностное отношение  и сократить на
и сократить на  .
.
3) Если  при
при  стремится к какому-то числу, то это число будет
стремится к какому-то числу, то это число будет  .
.
Далее группа самостоятельно формулирует и записывает в тетради
Физический смысл производной – это скорость изменения расстояния: s‘(t) = v(t).
(За бесконечно малое время прошел бесконечно малое расстояние. Спидометр машины показывает мгновенную скорость. Скорость в данный момент времени ).
Если производная положительная, то расстояние увеличивается, а если отрицательная, то расстояние уменьшается.
(Слайд 6)
Геометрический смысл: f‘(хо) – это коэффициент угла наклона касательной к оси Ох
f‘(хо) = k = tg α.
(Слайд 7)
Т.е. из геометрического смысла получается, что если существует производная в точке хо, то можно провести что? (обычно ученики говорят: что можно провести касательную в точке хо и наоборот – если можно провести касательную в точке хо, то в этой точке существует производная. На ошибку в формулировке пока не обращается внимание, фраза записывается на доске в таком виде и дальше продолжаются обсуждения.
записывается под определением на доске
…Если существует производная в точке хо, то можно провести касательную в точке хо. Наоборот — если можно провести (…) касательную в точке хо, то в этой точке существует производная.
Итак, подведём итог: вы сами дали мне определение производной, но встаёт вопрос: а всегда ли существует производная в точке?
Особое внимание обращается на моменты, когда касательная перпендикулярна оси Ох и параллельна оси Ох.
Всегда ли существует ли производная в точке хо?
Задается ряд вопросов:
|
Если касательная к графику функции будет убывающей, то каким будет угол между этой прямой и осью Ох?
|
Угол будет тупым.
|
|
Каким будет угловой коэффициент k ?
|
k < 0
|
|
Если касательная к графику функции будет возрастающей, то каким будет угол между этой прямой и осью Ох?
|
Угол будет острым.
|
|
Каким будет угловой коэффициент k ?
|
k > 0
|
|
Если касательная к графику функции будет параллельна оси Ох или совпадать с ней, то каким будет угол между этой прямой и осью Ох?
|
Угла не будет, вернее α = 0º
|
|
Чему равен тангенс угла наклона такой касательной?
|
tg 0º = 0
|
|
Чему равен угловой коэффициент k касательной, параллельной оси Ох?
|
Также не существует!
|
|
Чему равен угол наклона вертикальной касательной?
|
α = 90º
|
|
Чему равен тангенс угла наклона
вертикальной касательной?
|
tg 90º не существует. Почему? Потому, что cos 90º = 0…
|
|
Чему равен угловой коэффициент k вертикальной касательной?
|
Также не существует!
|
Давайте вернёмся к геометрическому смыслу производной: производная в точке равна угловому коэффициенту касательной, проведённой в этой точке f‘(хо) = k = tg α.
|
Если в точке можно провести невертикальную касательную, то в этой точке существует производная, и наоборот, если в точке существует производная, то в этой точке можно провести невертикальную касательную
|
5. Закрепление нового материала
Самостоятельная работа в группах (15-20 минут)
Вот теперь вы готовы к работе с производной и можете приступить к выполнению задания №2
Биологи

Пользуясь определением и схемой вычисления производной, найдите производную функции y = C.
Решение
y = C – постоянная линейная функция.
∆у = f(x +∆х) – f(x)= С – С = 0;
то у′ = 0.
Итак, ( С ) ′= 0.
Физики

Пользуясь определением и схемой вычисления производной, найдите производную функции y = kx + b.
Решение
y = kx + b – линейная функция.
Аргументу х дадим приращение ∆х, тогда
∆у = f(x + ∆х) – f(x)=
= k (x +∆х)+ b – (kx + b) = k∙x + k∆∙х – kx – b = k∆∙х
= k = k.
Итак, (kx + b)′ = k.
Математики

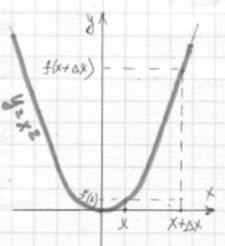
Лист №2: Пользуясь определением и схемой вычисления производной, найдите производную функции y = х2.
Решение
y = х2 .
Аргументу х дадим приращение ∆х, тогда
∆у = f(x + ∆х) – f(x)=
= (x +∆х)2 – х2 =
= х2+ 2∙х∙∆х + (∆х)2 – х2 = 2∙х∙∆х + (∆х)2 = ∆х∙(2х +∆х)
= 2х = 2х.
Итак, (х2 )′ = 2х.
6 этап. Закрепление нового понятия
1) Откройте учебники на стр. 106, № 189(а,б)
2) Возьмите лист № 3. Задания из ЕГЭ
Лист № 3.
1. Задание 7 (№ 9649)
На рисунке изображены график функции y = f(x) и
касательная к нему в точке с абсциссой x0 . Найдите
значение производной функции f = (x) в точке x0 .

2. Задание B7 (№ 6399)
На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции  положительна.
положительна.

7 этап. Итог урока
8 этап. Домашнее задание
№188 (б)
Постройте график функции f и проведите к нем касательную, проходящую через точки с абсциссой x0. Пользуясь рисунком, определите знак углового коэффициента этой касательной.
б) 
№189 (в, г)
Определите знак углового коэффициента касательной, проведенной к графику функции через точки с абсциссой  (если касательная существует).
(если касательная существует).

Просмотр содержимого документа
«Тема урока: Понятие о производной.»
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Понятие о производной.
Тип урока - урок изучения нового материала.
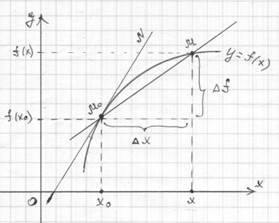
Пусть дан график функции у=f(x).
Рассмотрим точку М0 с абсциссой xo. Пусть ∆х – это изменение абсциссы от точки xo до х, т.е. ∆х = х – xo , M0М – секущая, M0N – касательная.
Найдите:
а) угловой коэффициент секущей (это средняя скорость изменения функции);
б) угловой коэффициент касательной (подсказка: касательная – это предельное положение секущей)
Решение: у= f(x) – заданная функция, ∆х = х – xo – изменение абсциссы от точки xo до х.
vср = 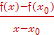 . В нашем случае kсек =
. В нашем случае kсек =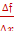
При х→х0 (или ∆х →0) будет f(x)→f(x0), следовательно, M0М→ M0N.
Тогда k кас = 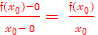 .
.
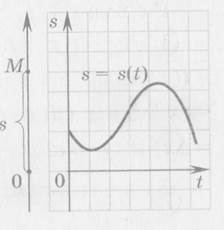
Рассмотрим движение материальной точки М по прямой с выбранным на ней началом отсчета – точкой О. Расстояние от начала отсчета до точки М в каждый момент времени t обозначим буквой s. Тогда движение точки М будет описываться функцией
s = s (t), t[ t0 ; t].
Найдите:
а) среднюю скорость за отрезок [t0 ; t];
б) скорость точки в момент времени t0 (мгновенную скорость).
Решение: За промежуток времени длительности t – t0 между моментами времени t0 и t точка проходит путь равный s(t) –s(t0 ).
Среднюю скорость получают, разделив перемещение материальной точки s на изменение времени, в течение которого оно совершено.
Тогда vср =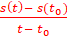 ;
;
Чем меньше рассматриваемый промежуток времени, тем точнее можно охарактеризовать движение. А мгновенной скоростью называется число к которому стремится разностное отношение средней скорости за промежуток времени от t0 до t при t→ t0.
Тогда vмгн = 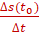 ,
,
Бактерии размножаются быстро и просто – они делятся пополам и при благоприятных условиях за сутки из одной бактерии могут образоваться десятки тысяч. Рост клеток бактерий в условиях ограниченности питательных веществ или пространства в течение начального интервала времени от t0 до t происходит по некоторому закону y = N(t).
Найдите:
а) среднюю скорость изменения количества бактерий за промежуток времени [t0 ; t];
б) скорость изменения количества точки в момент времени t0 (мгновенную скорость).
Решение: В физике для нахождения средней скорости делят длину перемещения тела s на время, в течение которого оно совершено,
т.е. vср =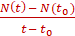 . В нашем случае vср =
. В нашем случае vср =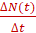 .
.
Мгновенной скоростью v(t0) в момент времени t0 является число к которому стремится разностное отношение средней скорости за промежуток времени от t0 до t при t→ t0.
Тогда vмгн = 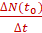 .
.
4. Изучение нового материала
Приращению аргумента соответствует «приращение функции», которое также обозначается с помощью заглавной греческой буквы «∆».
Вопрос: Скажите, а вы знаете, кто впервые стал использовать знак «∆» для обозначения разности аргументов?
- Да. Буква «∆» – одна из заглавных букв греческого алфавита ее стал использовать Эйлер (сер. 18 века).
Исходя из этого полученную формулу можно записать по-другому: или и прочитать так: число, к которому стремится разностное отношение 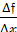 =
= 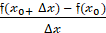 при
при 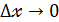 .
.
Поскольку многие задачи в различных областях науки в процессе решения приводят к такой же модели – этому отношению надо: дать название, дать обозначение и изучить его. Это мы с вами сейчас и сделаем.
(Слайд 4)
Определение: Производной функции 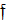 в точке
в точке 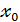 называется число, к которому стремится разностное отношение
называется число, к которому стремится разностное отношение 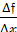 =
= 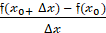 при
при 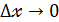 .
.
но обозначается по-разному:
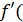 х),
х), 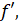 у′ – эти обозначения для производной ввел Жозеф Луи Лагранж
у′ – эти обозначения для производной ввел Жозеф Луи Лагранж
Это определение вы запишете в тетрадях.
Теперь посмотрите на ваши задачи и сформулируйте план нахождения производной.
(Учащиеся должны ответить):
(Слайд 5)
1. Задать функцию f(x).
Алгоритм нахождения производной (находим 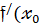 )):
)):
1) Задать приращение 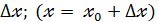 и вычислить
и вычислить 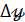 =
= 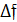 =
= 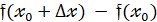 .
.
2) Найти разностное отношение 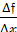 и сократить на
и сократить на 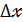 .
.
3) Если 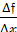 при
при 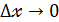 стремится к какому-то числу, то это число будет
стремится к какому-то числу, то это число будет 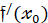 .
.
Далее группа самостоятельно формулирует и записывает в тетради
Физический смысл производной – это скорость изменения расстояния: s‘(t) = v(t).
(За бесконечно малое время прошел бесконечно малое расстояние. Спидометр машины показывает мгновенную скорость. Скорость в данный момент времени ).
Если производная положительная, то расстояние увеличивается, а если отрицательная, то расстояние уменьшается.
(Слайд 6)
Геометрический смысл: f‘(хо) – это коэффициент угла наклона касательной к оси Ох
f‘(хо) = k = tg α.
(Слайд 7)
Т.е. из геометрического смысла получается, что если существует производная в точке хо, то можно провести что? (обычно ученики говорят: что можно провести касательную в точке хо и наоборот – если можно провести касательную в точке хо, то в этой точке существует производная. На ошибку в формулировке пока не обращается внимание, фраза записывается на доске в таком виде и дальше продолжаются обсуждения.
записывается под определением на доске
…Если существует производная в точке хо, то можно провести касательную в точке хо. Наоборот — если можно провести (…) касательную в точке хо, то в этой точке существует производная.
Итак, подведём итог: вы сами дали мне определение производной, но встаёт вопрос: а всегда ли существует производная в точке?
Особое внимание обращается на моменты, когда касательная перпендикулярна оси Ох и параллельна оси Ох.
Всегда ли существует ли производная в точке хо?
Задается ряд вопросов:
| Если касательная к графику функции будет убывающей, то каким будет угол между этой прямой и осью Ох? | Угол будет тупым. |
| Каким будет угловой коэффициент k ? | k |
| Если касательная к графику функции будет возрастающей, то каким будет угол между этой прямой и осью Ох? | Угол будет острым. |
| Каким будет угловой коэффициент k ? | k 0 |
| Если касательная к графику функции будет параллельна оси Ох или совпадать с ней, то каким будет угол между этой прямой и осью Ох? | Угла не будет, вернее α = 0º |
| Чему равен тангенс угла наклона такой касательной? | tg 0º = 0 |
| Чему равен угловой коэффициент k касательной, параллельной оси Ох? | Также не существует! |
| Чему равен угол наклона вертикальной касательной? | α = 90º |
| Чему равен тангенс угла наклона вертикальной касательной? | tg 90º не существует. Почему? Потому, что cos 90º = 0… |
| Чему равен угловой коэффициент k вертикальной касательной? | Также не существует! |
Давайте вернёмся к геометрическому смыслу производной: производная в точке равна угловому коэффициенту касательной, проведённой в этой точке f‘(хо) = k = tg α.
| Если в точке можно провести невертикальную касательную, то в этой точке существует производная, и наоборот, если в точке существует производная, то в этой точке можно провести невертикальную касательную |
5. Закрепление нового материала
Самостоятельная работа в группах (15-20 минут)
Вот теперь вы готовы к работе с производной и можете приступить к выполнению задания №2
Биологи
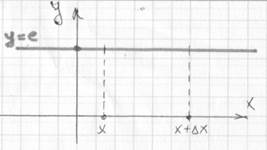
Пользуясь определением и схемой вычисления производной, найдите производную функции y = C.
Решение
y = C – постоянная линейная функция.
∆у = f(x +∆х) – f(x)= С – С = 0;
то у′ = 0.
Итак, ( С ) ′= 0.
Физики
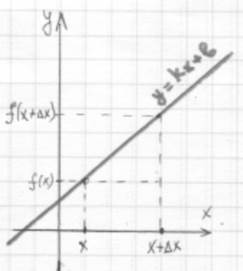
Пользуясь определением и схемой вычисления производной, найдите производную функции y = kx + b.
Решение
y = kx + b – линейная функция.
Аргументу х дадим приращение ∆х, тогда
∆у = f(x + ∆х) – f(x)=
= k (x +∆х)+ b – (kx + b) = k∙x + k∆∙х – kx – b = k∆∙х
= k = k.
Итак, (kx + b)′ = k.
Математики
Лист №2: Пользуясь определением и схемой вычисления производной, найдите производную функции y = х2.
Решение
y = х2 .
Аргументу х дадим приращение ∆х, тогда
∆у = f(x + ∆х) – f(x)=
= (x +∆х)2 – х2 =
= х2+ 2∙х∙∆х + (∆х)2 – х2 = 2∙х∙∆х + (∆х)2 = ∆х∙(2х +∆х)
= 2х = 2х.
Итак, (х2 )′ = 2х.
6 этап. Закрепление нового понятия
1) Откройте учебники на стр. 106, № 189(а,б)
2) Возьмите лист № 3. Задания из ЕГЭ
Лист № 3.
1. Задание 7 (№ 9649)
На рисунке изображены график функции y = f(x) и
касательная к нему в точке с абсциссой x0 . Найдите
значение производной функции f = (x) в точке x0 .

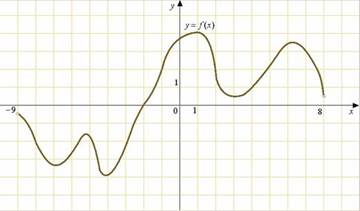
2. Задание B7 (№ 6399)
На рисунке изображен график функции 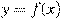 , определенной на интервале
, определенной на интервале 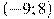 . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции 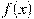 положительна.
положительна.
7 этап. Итог урока
8 этап. Домашнее задание
№188 (б)
Постройте график функции f и проведите к нем касательную, проходящую через точки с абсциссой x0. Пользуясь рисунком, определите знак углового коэффициента этой касательной.
б) 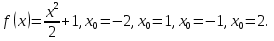
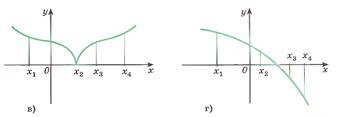
№189 (в, г)
Определите знак углового коэффициента касательной, проведенной к графику функции через точки с абсциссой 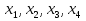 (если касательная существует).
(если касательная существует).







 . В нашем случае kсек =
. В нашем случае kсек =
 .
.
 ;
; ,
, . В нашем случае vср =
. В нашем случае vср = .
. .
. =
=  при
при  .
. в точке
в точке  называется число, к которому стремится разностное отношение
называется число, к которому стремится разностное отношение  х),
х),  у′ – эти обозначения для производной ввел Жозеф Луи Лагранж
у′ – эти обозначения для производной ввел Жозеф Луи Лагранж )):
)): и вычислить
и вычислить  =
=  =
=  .
. .
. .
.



 , определенной на интервале
, определенной на интервале  . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции  положительна.
положительна.

 (если касательная существует).
(если касательная существует).


















