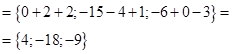Тема: "Вектора"

Инструкционная карта № 11

Тақырыбы/ Тема: «Прямоугольная система координат в пространстве. Действия над векторами, заданными координатами; формулы для вычисления длины вектора; угол между векторами; расстояние между двумя точками ».

Мақсаты/ Цель:

1. Познакомить учащихся с прямоугольной системой координат в пространстве, с действиями над векторами в координатах, углом между векторами и длиной вектора. Уметь применять эти понятия и формулы при решении задач.

2. Создать условия для развития умения устанавливать единые общие признаки и свойства целого, составлять план деятельности (сравнивать, анализировать).

3. Создать атмосферу коллективного поиска, эмоциональной приподнятости, радости познания трудностей.

Теоретический материал:

Если через точку О в пространстве мы проведем три перпендикулярные прямые, назовем их, выберем направление, обозначим единичные отрезки, то мы получим прямоугольную систему координат в пространстве. Оси координат называются так: Ох – ось абсцисс, Оy – ось ординат и Оz – ось аппликат. Вся система координат обозначается – Oxyz. Таким образом, появляются три координатные плоскости: Оxy, Оxz, Оyz.

Приведем пример построения точки В(4;3;5) в прямоугольной системе координат

(см. Рис. 1).

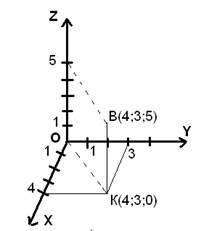
Рис. 1. Построение точки B в пространстве

Первая координата точки B – 4, поэтому откладываем на Ox 4, проводим прямую параллельно оси Oy до пересечения с прямой, проходящей через у=3. Таким образом, мы получаем точку K. Эта точка лежит в плоскости Oxy и имеет координаты K(4;3;0). Теперь нужно провести прямую параллельно оси Oz. И прямую, которая проходит через точку с аппликатой 5 и параллельна диагонали параллелограмма в плоскости Oxy. На их пересечении мы получим искомую точку B.

2. Возьмем точку A(x₁;y₁;z₁) и точку B(x₂;y₂;z₂) (см. рис. 2). Представим вектор 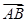как разность векторов  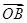и 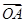по свойству векторов. Причем,  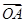и 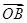- радиус-векторы, и их координаты совпадают с координатами концов этих векторов. Тогда мы можем представить координаты вектора  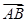как разность соответствующих координат векторов  и : 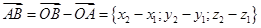. Таким образом, координаты вектора мы можем выразить через координаты конца и начала вектора.

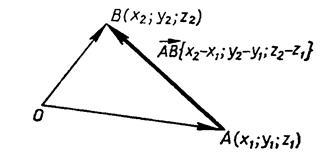
Рис. 2.

3. Рассмотрим примеры, иллюстрирующие свойства векторов и их выражение через координаты. Возьмем векторы 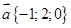, , 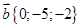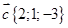. Нас спрашивают вектор 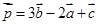. В данном случае найти  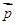это значит найти координаты вектора, которые полностью его определяют. Подставляем в выражение вместо векторов соответственно их координаты. Получаем:

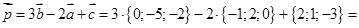
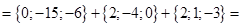
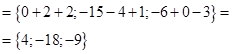
4. Пример. Задача на нахождение координат середины отрезка (рис. 3). Даны две точки: A(x₁;y₁z₁), B(x₂;y₂;z₂), C – середина AB. Найти: C(x;y;z).

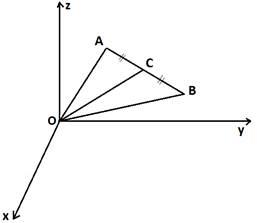
Рис. 3. Координаты середины отрезка

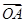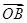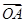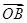Решение: Обозначим в пространстве точки A, B и С – середину отрезка AB. Вектор  является половиной суммы векторов  и , потому что OC – это половина диагонали параллелограмма, построенного на векторах   и . Координаты точки C находятся, как полусумма координат концов отрезка AB - точек A и B. Найдем координаты точки С:

, , .

Задача. Дано: M(-4;7;0), N(0;-1;2), C – середина MN. Найти: координаты точки C.

Решение: Сначала найдем координаты точки C. Ее координаты равны полусумме соответствующих координат. .

5. Пример . Задача на нахождение модуля вектора через его координаты.

Если у нас есть вектор , то его модуль вычисляется по формуле: .

.

6. ЗАДАЧА: Найти скалярное произведение векторов:

б)  и , если даны точки 

Решение: 

А тут речь идёт о точках и векторах пространства. Сначала найдём векторы:
 
Надеюсь, эта простейшая задача у вас уже отработана.

По формуле  вычислим скалярное произведение:

К слову: скалярное произведение положительно, значит, угол между пространственными векторами  является острым.

7. Пусть 

Выразите  в координатах.

Имеем .

Практическая часть:

Задача: В треугольнике с вершинами А(х₁;у₁;z₁), В(х₂;у₂; z₂) и С(х₃;у₃; z₃). Найдите координаты вектора , длину вектора , вектор координаты точки D(х₀;у₀; z₀) – середина стороны ВС, cos A, площадь треугольника АВС. Сделай чертеж.

Контрольные вопросы:

1. Что такое вектор и как его обозначают?

2. Какие векторы называются равными?

3. Как строится прямоугольная система координат в пространстве?

4. Как находятся координаты вектора по координатам его концов?

5. Как находятся координаты суммы и разности векторов?

6. Как умножается число на вектор?

7. Как найти расстояние между точками в пространстве?

8. Что такое скалярное произведение векторов?

9. Напишите формулу скалярного произведения в координатах.