Теорема Фалеса (теория)

Теорема Фалеса

Урок геометрии в 8 классе

Учитель математики ГБОУ Школа №15

Дмитрий Вадимович Лабзин

Теорема. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

l 2

l 1

A 1

B 1

По условию: A 1 A 2 =A 2 A 3 =A 3 A 4 =A 4 A 5 =A 5 A 6 =A 6 A 7

A 2

B 2

A 3

B 3

A 4

B 4

Надо доказать:

B 1 B 2 =B 2 B 3 =B 3 B 4 =B 4 B 5 =B 5 B 6 =B 6 B 7

B 5

A 5

A 6

B 6

B 7

A 7

Доказательство.

1) Пусть

l 2

l 1

A 1

B 1

Так как и ; …, то - параллелограммы. Следовательно,

… (по свойству параллелограмма) и … (по условию), то …

A 2

B 2

A 3

B 3

A 4

B 4

A 5

B 5

A 6

B 6

A 7

B 7

l 2

l 3

l 1

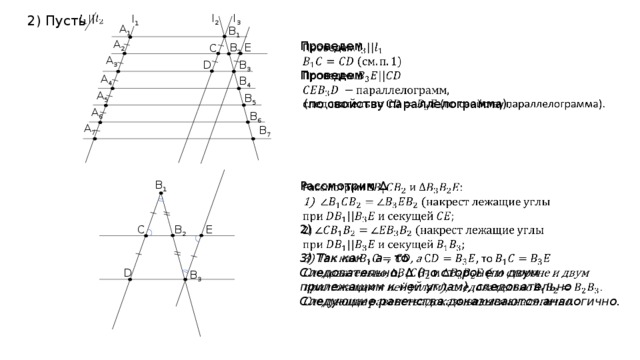
2) Пусть

A 1

B 1

A 2

Проведем

Проведем

(по свойству параллелограмма).

B 2

Е

C

A 3

B 3

D

A 4

B 4

A 5

B 5

A 6

B 6

A 7

B 7

B 1

Рассмотрим Δ

2)

3) Так как , а , то

Следовательно, Δ (по стороне и двум прилежащим к ней углам), следовательно

Следующие равенства доказываются аналогично.

C

E

B 2

D

B 3