Теорема косинусов 9 класс

Теорема косинусов

Теорема (к осинусов) . Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними ,

c 2 = a 2 + b 2 – 2 ab cos C .

Доказательство: Обозначим АВ = с , ВС = а , АС = b . Из вершины А опустим перпендикуляр А D . Тогда АD = b sin C , CD = b cos C , BD = a – b cos C . По теореме Пифагора имеем c 2 = ( a – b cos C ) 2 + ( b sin C ) 2 = a 2 – 2 ab cos C + b 2 cos 2 C + b 2 sin 2 C = a 2 + b 2 – 2 ab cos C .

В режиме слайдов ответы появляются после кликанья мышкой

Самостоятельно рассмотрите случаи прямого и тупого угла С .

Упражнение 1

В треугольнике ABC AC = BC = 1, угол C равен 30 о . Найдите AB .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: .

2

Упражнение 2

В треугольнике ABC AC = BC , угол C равен 30 о , AB = 1. Найдите AC .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: .

3

Упражнение 3

В треугольнике ABC AC = BC = 1, угол C равен 45 о . Найдите AB .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: .

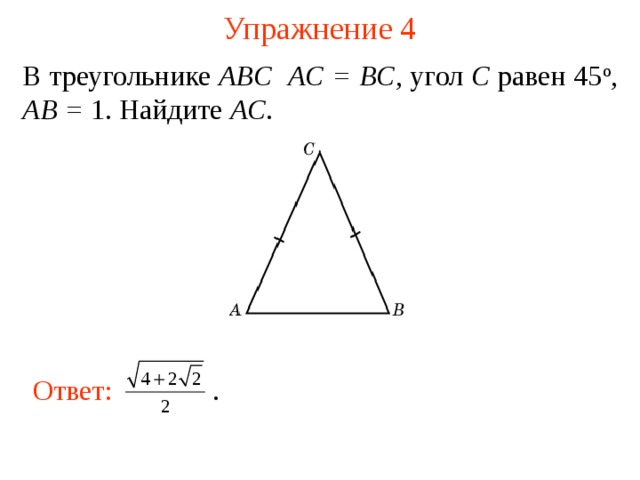
Упражнение 4

В треугольнике ABC AC = BC , угол C равен 45 о , AB = 1. Найдите AC .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: .

5

Упражнение 5

В треугольнике ABC AC = BC = 1, угол C равен 150 о . Найдите AB .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: .

6

Упражнение 6

В треугольнике ABC AC = BC , угол C равен 150 о , AB = 1. Найдите AC .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: .

7

Упражнение 7

В треугольнике ABC AC = BC = 1, угол C равен 135 о . Найдите AB .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: .

Упражнение 8

В треугольнике ABC AC = BC , угол C равен 135 о , AB = 1. Найдите AC .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: .

9

Упражнение 9

Даны три стороны треугольника a = 2, b = 3, c = 4. Найдите косинусы его углов A , B , C .

Ответ: cos A = , cos B = , cos C = .

В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 10

В треугольнике АВС АВ = 12 см, АС = 8 см, угол A равен 60 о . Найдите третью сторону.

Ответ:

В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 11

Найдите сторону треугольника, лежащую против угла в 120 о , если прилежащие к нему стороны равны: а) 6 см и 10 см; б) 14 мм и 16 мм.

Ответ: а) 14 см;

б) 26 мм.

В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 12

При каких значениях угла А квадрат стороны треугольника, лежащей против этого угла: а) меньше суммы квадратов двух других сторон; б) равен сумме квадратов двух других сторон; в) больше суммы квадратов двух других сторон?

Ответ: а) острый;

б) прямой;

в) тупой .

В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 13

Не вычисляя углы треугольника, укажите его вид (относительно углов), если стороны треугольника равны: а) 7, 8, 12; б) 0,3, 0,4, 0,5; в) 13, 14, 15.

Ответ: а) Тупоугольный;

б) прямоугольный;

В режиме слайдов ответы появляются после кликанья мышкой

в) остроугольный.

Упражнение 14

Как расположен центр описанной окружности относительно треугольника, стороны которого равны: а) 6, 8, 10; б) 4, 5, 6; в) 3, 4, 6?

Ответ: а) На стороне треугольника;

б) внутри треугольника;

В режиме слайдов ответы появляются после кликанья мышкой

в) вне треугольника.

Упражнение 15

Даны диагонали параллелограмма с и d и угол между ними . Найдите стороны параллелограмма.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

16

Упражнение 16

Даны стороны параллелограмма а и b и один из его углов . Найдите диагонали параллелограмма.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

17

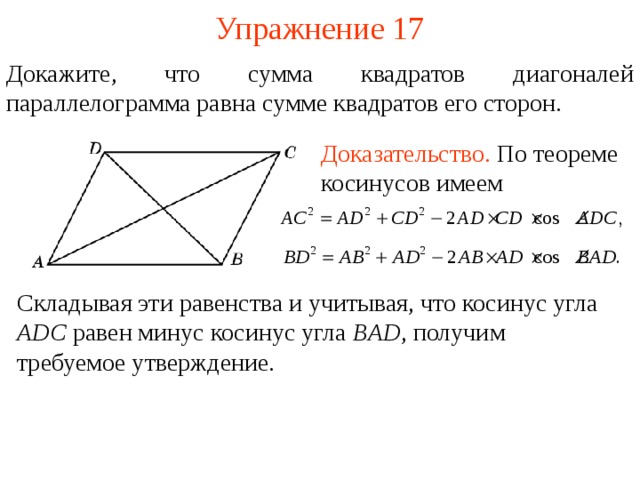
Упражнение 17

Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Доказательство. По теореме косинусов имеем

Складывая эти равенства и учитывая, что косинус угла ADC равен минус косинус угла BAD , получим требуемое утверждение.

В режиме слайдов ответы появляются после кликанья мышкой

18

Упражнение 18

Стороны параллелограмма равны 30 мм и 35 мм, одна диагональ 55 мм. Найдите другую диагональ.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 35 мм.

Упражнение 1 9

Пусть в треугольнике ABC AB = c , AC = b , BC = a . Докажите, что для медианы m c , проведенной из вершины C , имеет место формула

Доказательство. По теореме косинусов, примененной к треугольникам ACD и BCD , имеем:

Складывая эти равенства, получим равенство

из которого непосредственно следует искомая формула.

Упражнение 20

Стороны треугольника равны 11, 12 и 13. Найдите медиану, проведенную к большей стороне.

Ответ. 9,5.

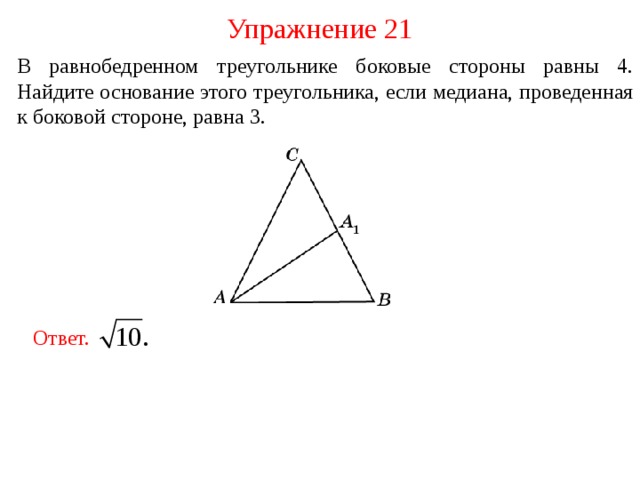
Упражнение 21

В равнобедренном треугольнике боковые стороны равны 4. Найдите основание этого треугольника, если медиана, проведенная к боковой стороне, равна 3.

Ответ.

Упражнение 22

Пусть в треугольнике ABC AC = b , BC = a . Докажите, что для биссектрисы l c , проведенной из вершины C , имеет место формула

где c’ , c’’ – отрезки на которые биссектриса делит сторону AB

Доказательство. По теореме косинусов, примененной к треугольникам ACD и BCD , имеем:

Умножим первое равенство на a , второе на b и вычтем из первого равенства второе. Делая тождественные преобразования, получим равенство из которого непосредственно следует искомая формула.

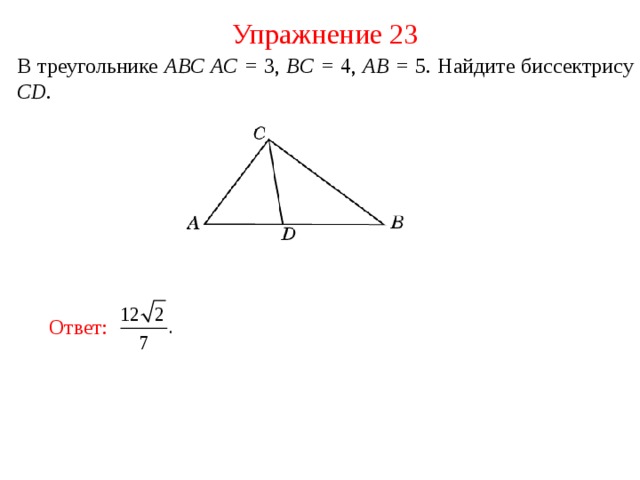
Упражнение 23

В треугольнике ABC AC = 3, BC = 4, AB = 5 . Найдите биссектрису CD .

Ответ :

Упражнение 24

В треугольнике ABC AC = BC = 20 , AB = 5, Найдите биссектрису AD .

Ответ : 6.

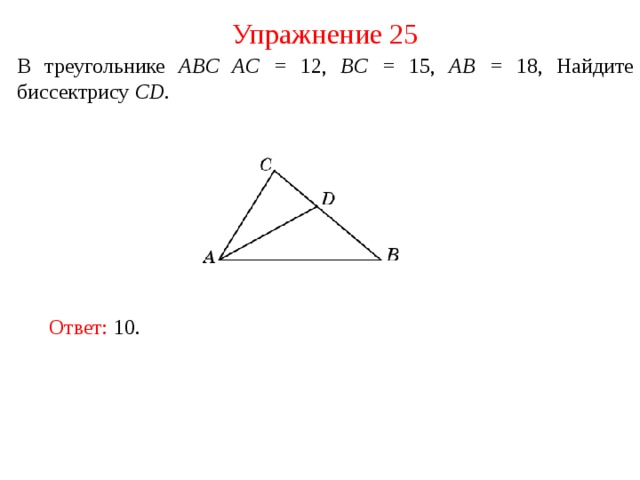
Упражнение 25

В треугольнике ABC AC = 12, BC = 15 , AB = 18 , Найдите биссектрису С D .

Ответ : 10.

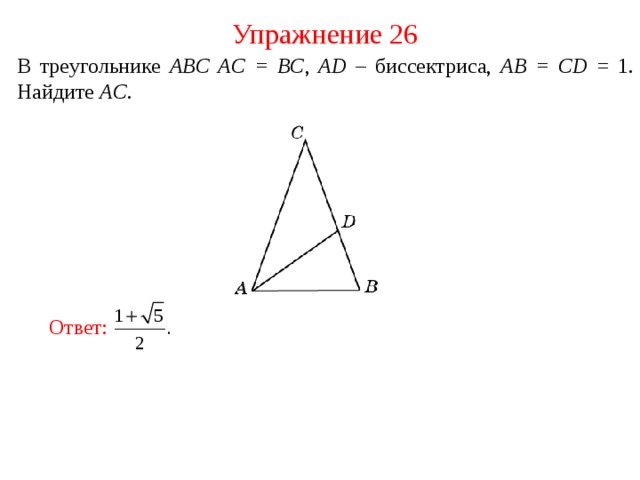
Упражнение 26

В треугольнике ABC AC = BC , AD – биссектриса, AB = CD = 1. Найдите AC .

Ответ :

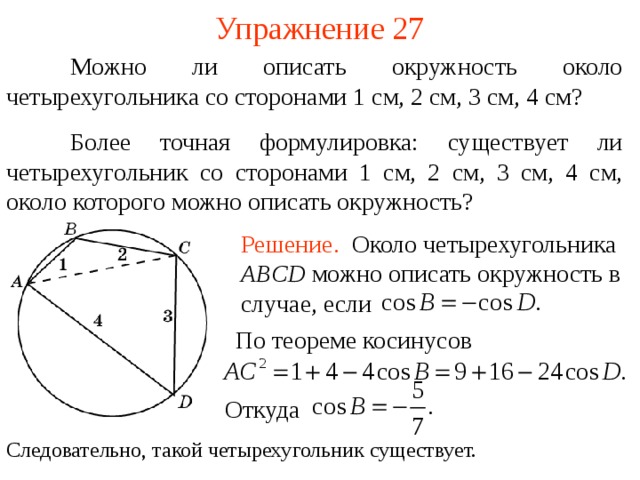
Упражнение 27

Можно ли описать окружность около четырехугольника со сторонами 1 см, 2 см, 3 см, 4 см?

Более точная формулировка: существует ли четырехугольник со сторонами 1 см, 2 см, 3 см, 4 см, около которого можно описать окружность?

Решение. Около четырехугольника ABCD можно описать окружность в случае, если

В режиме слайдов ответы появляются после кликанья мышкой

По теореме косинусов

Откуда

Следовательно, такой четырехугольник существует.